https://codeforc.es/problemset/problem/1216/F
有直线上n个位置,每个位置上可以花费i的代价使得联网,某些位置可以放置路由器,放路由器的代价也是i,放置了路由器以后,可以让[i-k,i+k]的范围内上网,要求每台电脑都可以上网,最少需要多少代价。
思路: 动态规划+贪心+线段树维护
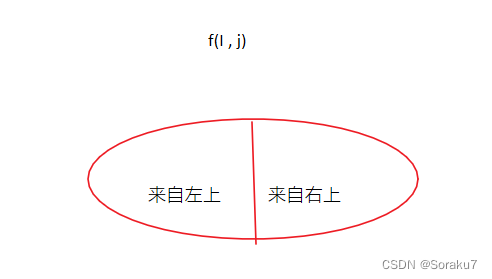
f[i]表示前i个电脑上网所需要的最小费用。
转移的时候分为两种情况。
1. 第i台电脑独立上网,花费的代价是i
f[i-1]+i
2 第i台电脑通过前面某台电脑的路由器上网,根据贪心的原则,肯定是在[i-k,i-1]里面位置最小的可以放路由器的地方,一来覆盖的范围可以更大,二来费用更低。
我们可以通过线段树里面维护这个位置,二分来查找。
转移的时候,注意由于区间可以重叠,所以我们要求一个区间最小值来进行转移,还是用线段树来做。


1 #include<bits/stdc++.h> 2 using namespace std; 3 #define LL long long 4 #define lc (x<<1) 5 #define rc (x<<1|1) 6 #define mid (l+r)/2 7 int const N=200000+10; 8 char s[N]; 9 LL f[N],v[N<<2]; 10 int n,k,sum[N<<2],pos[N<<2]; 11 void build(int x,int l,int r){ 12 if(l==r){ 13 sum[x]=s[l]=='1'; 14 if(sum[x]) pos[x]=l; 15 return ; 16 } 17 build(lc,l,mid); 18 build(rc,mid+1,r); 19 sum[x]=sum[lc]+sum[rc]; 20 if(pos[lc]) pos[x]=pos[lc]; 21 else pos[x]=pos[rc]; 22 } 23 int query(int x,int l,int r,int ll,int rr){ 24 if(ll<=l && r<=rr){ 25 return pos[x] ; 26 } 27 int t1=0,t2=0; 28 if(ll<=mid) t1=query(lc,l,mid,ll,rr); 29 if(t1) return t1; 30 if(rr>mid) t2=query(rc,mid+1,r,ll,rr); 31 return t2; 32 } 33 void insert(int x,int l,int r,int p,LL tv){ 34 if(l==r){ 35 v[x]=tv; 36 return; 37 } 38 if(p<=mid) insert(lc,l,mid,p,tv); 39 else insert(rc,mid+1,r,p,tv); 40 v[x]=min(v[lc],v[rc]); 41 } 42 LL ask(int x,int l,int r,int ll,int rr){ 43 if(ll>rr) return 1e18; 44 if(ll<=l && r<=rr) { 45 return v[x]; 46 } 47 LL res=1e18; 48 if(ll<=mid) res=min(res,ask(lc,l,mid,ll,rr)); 49 if(rr>mid) res=min(res,ask(rc,mid+1,r,ll,rr)); 50 return res; 51 } 52 int main(){ 53 scanf("%d%d",&n,&k); 54 scanf("%s",s+1); 55 build(1,1,n); 56 for(int i=1;i<=n;i++){ 57 f[i]=f[i-1]+i; 58 int t=query(1,1,n,max(1,i-k),i); 59 if(t) { 60 int p=max(1,t-k-1); 61 LL tmp=ask(1,1,n,p,i-1); 62 if(t-k-1<1) tmp=0; 63 f[i]=min(f[i],tmp+t); 64 } 65 insert(1,1,n,i,f[i]); 66 } 67 cout<<f[n]<<endl; 68 return 0; 69 }