[R语言]稳健回归

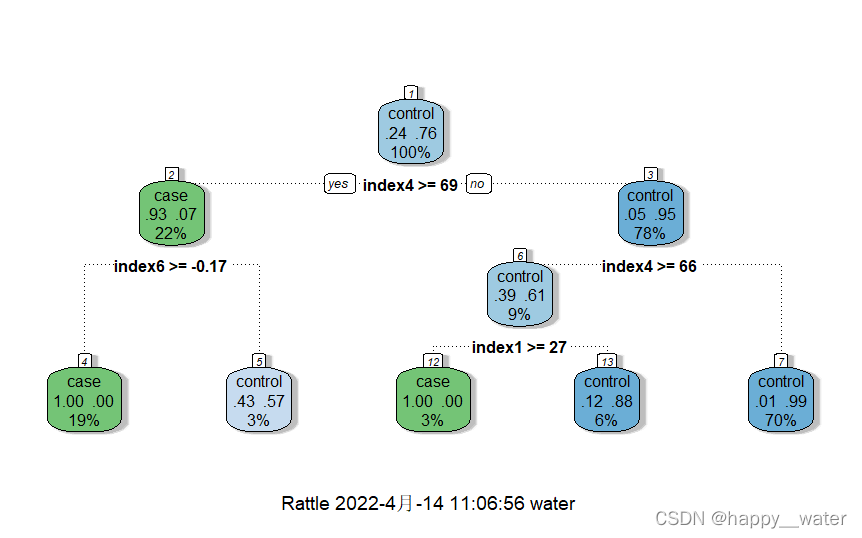
原文来自：稳健回归

INTRODUCTION

我们以线性回归中的一些概念开始关于稳健回归的讨论。

残差： 预测值（基于回归方程）与实际观察值之间的差。

离群值： 在线性回归中，离群值是具有大量残差的观察值。换句话说，鉴于其对预测变量的价值，这是一个因变量不寻常的观察结果。离群值可能表示样本特性，或者可能表示数据输入错误或其他问题。

杠杆： 对预测变量具有极高价值的观察点具有很高的杠杆作用。杠杆作用是对自变量偏离均值的程度的度量。高杠杆点可能会对回归系数的估计产生很大影响。

影响： 如果删除观察结果会显着改变回归系数的估计值，则认为该观察结果具有影响力。可以将影响视为杠杆和离群值的产物。

库克距离： 一种结合了杠杆作用和观测值残差信息的度量。

可以在使用最小二乘回归的任何情况下使用稳健回归。在拟合最小二乘回归时，我们可能会发现一些离群值或高杠杆点。我们已经确定这些数据点不是数据输入错误，也不是来自与我们大多数数据不同的总体。因此，我们没有令人信服的理由将它们排除在分析之外。稳健的回归可能是一个很好的策略，因为这是从完全排除这些异常点与包括所有数据点OLS回归的折中方案。稳健回归的想法是根据这些观察的表现如何对观察进行不同的加权。粗略地说，它是加权和最小二乘回归的一种形式。

在MASS包中，使用rlm在命令可以实现稳健回归的几个版本。在此，我们将展示使用 Huber 和 bisquare权重的M估计。M估计定义了权重函数，使估计方程变为 $\sum_{i=1}^{n} w_i (y_i - x^Tb)x^T = 0$ . 但是这一权重又取决于残差。这一方程使用迭代重加权最小平方法（Iteratively Reweighted Least Squares，IRLS）求解。例如，第j步迭代的稀疏矩阵为： $B_j =[X^TW_{j-1}X]^{-1}X^TW_{j-1}Y$ . 迭代重复该过程一直持续到收敛为止。在Huber加权中，残差小的观测值的权重为1，而残差越大，权重就越小。这由权重函数的定义所决定的。如果使用bisquare加权，所有具有非零残差的情况，权重都有所降低。

示例数据说明

对于下面的数据分析，我们将使用 Alan Agresti 和Barbara Finlay（Prentice Hall，1997）在《社会科学统计方法》第三版中出现的犯罪数据集。变量包括各州 ID（sid），州名（state），每10万人的暴力罪犯（crime），每1,000,000人中的谋杀罪犯（murder），居住在大都市区的比例（pctmetro），白人的比例（pctwhite），高中或以上学历的人口百分比（pcths），生活在贫困线以下的人口百分比（poverty）和单亲父母的人口百分比（single）。它有51个观测值。我们将使用poverty 和single预测crime.

library(foreign)
library(MASS)cdata <- read.dta("https://stats.idre.ucla.edu/stat/data/crime.dta")
summary(cdata)

结果为

      sid          state               crime            murder          pctmetro         pctwhite    Min.   : 1.0   Length:51          Min.   :  82.0   Min.   : 1.600   Min.   : 24.00   Min.   :31.80  1st Qu.:13.5   Class :character   1st Qu.: 326.5   1st Qu.: 3.900   1st Qu.: 49.55   1st Qu.:79.35  Median :26.0   Mode  :character   Median : 515.0   Median : 6.800   Median : 69.80   Median :87.60  Mean   :26.0                      Mean   : 612.8   Mean   : 8.727   Mean   : 67.39   Mean   :84.12  3rd Qu.:38.5                      3rd Qu.: 773.0   3rd Qu.:10.350   3rd Qu.: 83.95   3rd Qu.:92.60  Max.   :51.0                      Max.   :2922.0   Max.   :78.500   Max.   :100.00   Max.   :98.50  pcths          poverty          single     Min.   :64.30   Min.   : 8.00   Min.   : 8.40  1st Qu.:73.50   1st Qu.:10.70   1st Qu.:10.05  Median :76.70   Median :13.10   Median :10.90  Mean   :76.22   Mean   :14.26   Mean   :11.33  3rd Qu.:80.10   3rd Qu.:17.40   3rd Qu.:12.05  Max.   :86.60   Max.   :26.40   Max.   :22.10

使用普通最小二乘回归

summary(ols <- lm(crime ~ poverty + single, data = cdata))

结果为

Call:
lm(formula = crime ~ poverty + single, data = cdata)Residuals:Min      1Q  Median      3Q     Max 
-811.14 -114.27  -22.44  121.86  689.82 Coefficients:Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1368.189    187.205  -7.308 2.48e-09 ***
poverty         6.787      8.989   0.755    0.454    
single        166.373     19.423   8.566 3.12e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 243.6 on 48 degrees of freedom
Multiple R-squared:  0.7072,	Adjusted R-squared:  0.695 
F-statistic: 57.96 on 2 and 48 DF,  p-value: 1.578e-13

我们来看一下普通最小二乘回归的诊断图

opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(ols, las = 1)

结果如下：
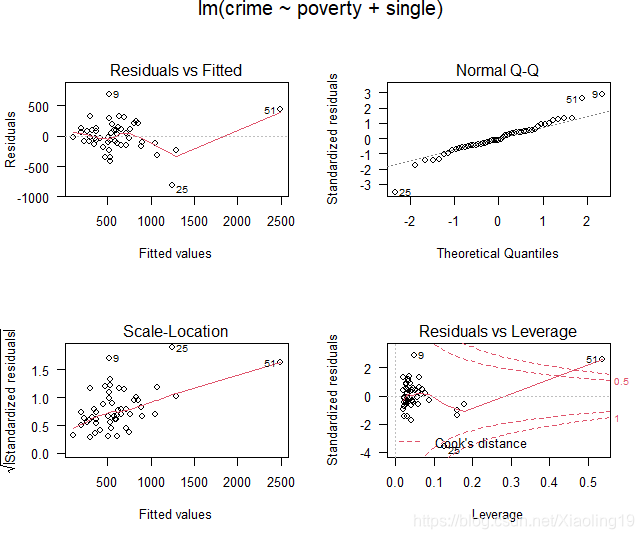回归诊断从这些图中，我们可以确定观测值9、25和51对我们的模型可能存在问题。我们可以查看这些观察值，以了解它们所代表的状态。

par(opar)
cdata[c(9, 25, 51), 1:2]

结果为

   sid state
9    9    fl
25  25    ms
51  51    dc

哥伦比亚特区，佛罗里达州和密西西比州的杠杆率很高或残差很大。我们可以显示具有较大Cook值的观测值。常规的截止点是 $n / 4$ ， $n$ 是数据集中的观察数。我们将使用此条件来选择要显示的值。

d1 <- cooks.distance(ols)
r <- stdres(ols)
a <- cbind(cdata, d1, r)
a[d1 > 4/51, ]

结果为

   sid state crime murder pctmetro pctwhite pcths poverty single        d1         r
1    1    ak   761    9.0     41.8     75.2  86.6     9.1   14.3 0.1254750 -1.397418
9    9    fl  1206    8.9     93.0     83.5  74.4    17.8   10.6 0.1425891  2.902663
25  25    ms   434   13.5     30.7     63.3  64.3    24.7   14.7 0.6138721 -3.562990
51  51    dc  2922   78.5    100.0     31.8  73.1    26.4   22.1 2.6362519  2.616447

因为DC不是州，所以我们可能应该先删除DC。我们将其包括在分析中只是为了表明它具有大的Cook距离并演示如何使用rlm。现在我们来看一下残差。我们将生成一个名为的新变量absr1，它是残差的绝对值（因为残差的符号无关紧要）。然后，我们打印出具有最高绝对残差值的十个观测值。

rabs <- abs(r)
a <- cbind(cdata, d1, r, rabs)
asorted <- a[order(-rabs), ]
asorted[1:10, ]

结果为

   sid state crime murder pctmetro pctwhite pcths poverty single         d1         r     rabs
25  25    ms   434   13.5     30.7     63.3  64.3    24.7   14.7 0.61387212 -3.562990 3.562990
9    9    fl  1206    8.9     93.0     83.5  74.4    17.8   10.6 0.14258909  2.902663 2.902663
51  51    dc  2922   78.5    100.0     31.8  73.1    26.4   22.1 2.63625193  2.616447 2.616447
46  46    vt   114    3.6     27.0     98.4  80.8    10.0   11.0 0.04271548 -1.742409 1.742409
26  26    mt   178    3.0     24.0     92.6  81.0    14.9   10.8 0.01675501 -1.460885 1.460885
21  21    me   126    1.6     35.7     98.5  78.8    10.7   10.6 0.02233128 -1.426741 1.426741
1    1    ak   761    9.0     41.8     75.2  86.6     9.1   14.3 0.12547500 -1.397418 1.397418
31  31    nj   627    5.3    100.0     80.8  76.7    10.9    9.6 0.02229184  1.354149 1.354149
14  14    il   960   11.4     84.0     81.0  76.2    13.6   11.5 0.01265689  1.338192 1.338192
20  20    md   998   12.7     92.8     68.9  78.4     9.7   12.0 0.03569623  1.287087 1.287087

使用稳健回归

现在让我们运行第一个稳健的回归。通过迭代的重新加权最小二乘法（IRLS）进行稳健的回归。运行稳定回归的指令是rlm在MASS包。有几种加权功能可用于IRLS。在本示例中，我们将首先使用Huber权重。然后，我们将查看由IRLS流程创建的最终权重。这可能非常有用。

summary(rr.huber <- rlm(crime ~ poverty + single, data = cdata))

结果为

Call: rlm(formula = crime ~ poverty + single, data = cdata)
Residuals:Min      1Q  Median      3Q     Max 
-846.09 -125.80  -16.49  119.15  679.94 Coefficients:Value      Std. Error t value   
(Intercept) -1423.0373   167.5899    -8.4912
poverty         8.8677     8.0467     1.1020
single        168.9858    17.3878     9.7186Residual standard error: 181.8 on 48 degrees of freedom

我们来看一下各观测点的权重。

hweights <- data.frame(state = cdata$state, resid = rr.huber$resid, weight = rr.huber$w)
hweights2 <- hweights[order(rr.huber$w), ]
hweights2[1:15, ]

结果为

   state      resid    weight
25    ms -846.08536 0.2889618
9     fl  679.94327 0.3595480
46    vt -410.48310 0.5955740
51    dc  376.34468 0.6494131
26    mt -356.13760 0.6864625
21    me -337.09622 0.7252263
31    nj  331.11603 0.7383578
14    il  319.10036 0.7661169
1     ak -313.15532 0.7807432
20    md  307.19142 0.7958154
19    ma  291.20817 0.8395172
18    la -266.95752 0.9159411
2     al  105.40319 1.0000000
3     ar   30.53589 1.0000000
4     az  -43.25299 1.0000000

我们可以粗略地看到，随着绝对残差的减少，权重也会增加。换句话说，残差较大的情况倾向于权重降低。此输出向我们显示，密西西比州的观测值将被最大程度地降低权重。佛罗里达州的权重也将大大降低。上面未显示的所有观察值的权重均为1。在OLS回归中，所有情况的权重均为1。因此，稳健回归中权重接近1的案例越多，OLS和稳健回归的结果越接近。

接下来，让我们运行相同的模型，但是使用双向平方加权函数。同样，我们可以看一下权重。

rr.bisquare <- rlm(crime ~ poverty + single, data=cdata, psi = psi.bisquare)
summary(rr.bisquare)

结果为

Call: rlm(formula = crime ~ poverty + single, data = cdata, psi = psi.bisquare)
Residuals:Min      1Q  Median      3Q     Max 
-905.59 -140.97  -14.98  114.65  668.38 Coefficients:Value      Std. Error t value   
(Intercept) -1535.3338   164.5062    -9.3330
poverty        11.6903     7.8987     1.4800
single        175.9303    17.0678    10.3077Residual standard error: 202.3 on 48 degrees of freedom

我们来看一下各观测点的权重：

biweights <- data.frame(state = cdata$state, resid = rr.bisquare$resid, weight = rr.bisquare$w)
biweights2 <- biweights[order(rr.bisquare$w), ]
biweights2[1:15, ]

结果为

   state     resid      weight
25    ms -905.5931 0.007652565
9     fl  668.3844 0.252870542
46    vt -402.8031 0.671495418
26    mt -360.8997 0.731136908
31    nj  345.9780 0.751347695
18    la -332.6527 0.768938330
21    me -328.6143 0.774103322
1     ak -325.8519 0.777662383
14    il  313.1466 0.793658594
20    md  308.7737 0.799065530
19    ma  297.6068 0.812596833
51    dc  260.6489 0.854441716
50    wy -234.1952 0.881660897
5     ca  201.4407 0.911713981
10    ga -186.5799 0.924033113

我们可以看到，使用bisquare 加权函数比使用Huber 加权函数给密西西比州的加权显着更低，并且这两种不同加权方法的参数估计值也不同。在比较常规OLS回归和稳健回归的结果时，如果结果非常不同，最好使用稳健回归的结果。较大的差异表明模型参数受到异常值的高度影响。不同的权函数各有利弊。Huber权重可能会遇到严重的离群值，而Bisquare权重可能会难以收敛或可能产生多个解。

两次分析的结果有很大不同，尤其是在系数single和常数（intercept）方面。虽然通常我们对常量不感兴趣，但是如果将一个或两个预测变量居中，则该常量将很有用。另一方面，注意到这poverty两种分析在统计上都不显着，而single在两种分析中均显着。