请设计一个算法,将给定的表达式树(二叉树)转换成等价的中缀表达式(通过括号反映次序),并输出。例如,当下列两棵表达式树作为算法的输入时:
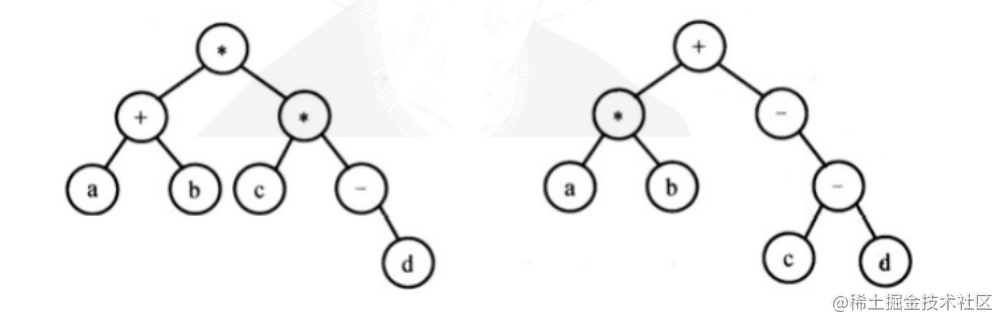
输出的等价中缀表达式分别为(a+b)(a(-d)) 和 (a * b)+(-(c-d))
二叉树结点定义如下:
typedef struct node
{char date[10]; //存储操作数或者操作符struct node *left, *right;
} BTree;要求:
(1) 给出算法的基本思想
(2) 根据设计思想,采用c/c++语言描述算法,关键之处给出注释
算法思想:基于二叉树的中缀遍历,添加适当括号,显然,表达式的最外层(对于根节点)及操作数
(对应叶节点)不需要添加括号(这句是答案说的,其实不太懂)
void B2E(BTree *root)
{B2E(root, 1);
}
void B2E(BTree *root, int deep)
{if (root == NULL)printf("NULL");else if (root->left == NULL && root->right == NULL) //叶节点printf("%s", root->data); //输出操作数else{if (deep > 1)printf("(");B2E(root->left, deep + 1);printf("%s", root->data); //输出操作符B2E(root->right, deep + 1);if (deep > 1)printf(")");}
}
解决方法:
(1)算法的基本设计思想
表达式树的中序序列加上必要的括号即为等价的中缀表达式。可以基
于二叉树的中序遍历策略得到所需的表达式。(3 分)
表达式树中分支结点所对应的子表达式的计算次序,由该分支结点所
处的位置决定。为得到正确的中缀表达式,需要在生成遍历序列的同
时,在适当位置增加必要的括号。显然,表达式的最外层(对应根结点)
及操作数(对应叶结点)不需要添加括号。(2 分)
(2)算法实现(10 分)
将二叉树的中序遍历递归算法稍加改造即可得本题答案。除根结点和
叶结点外,遍历到其他结点时在遍历其左子树之前加上左括号,在遍
历完右子树后加上右括号。