【设计目标】对双二阶环路滤波器进行时频域分析和处理的基本方法
【设计工具】MATLAB【设计要求】
1)分析典型的双二阶环路滤波器电路:低通、高通、带通、带阻
2)理论分析各滤波电路的系统函数
3)利用Matlab分析各滤波电路的系统函数的频率特性(幅频、相频)、零极点分布
4)分析不同频率正弦信号及其叠加信号通过各滤波器后,输入信号与输出信号的频谱,解释滤波器的性能;
5)分析各滤波器的单位冲击响应和阶跃响应曲线
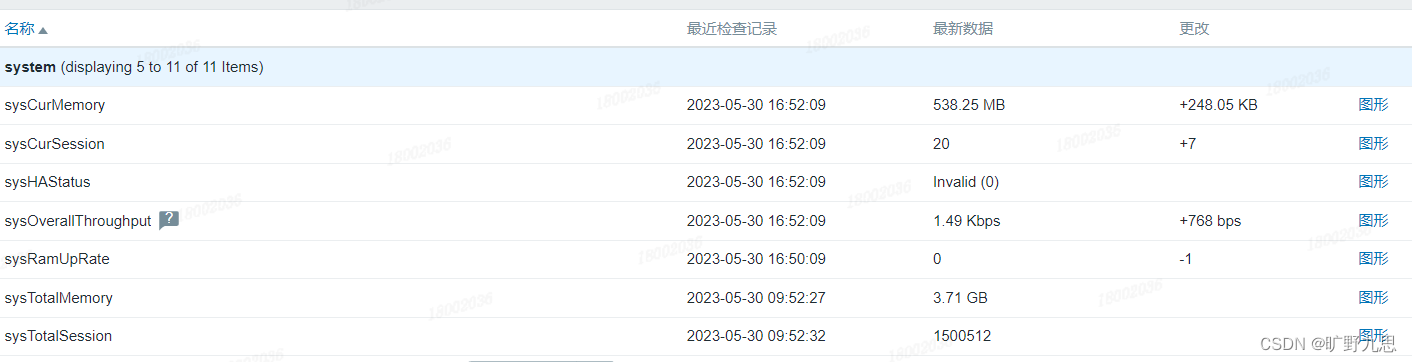
要求步骤,数据及分析
步骤:
- 理论分析各滤波电路的系统函数
双二阶环路滤波器是一种常见的滤波器电路,包括低通、高通、带通和带阻四种类型。这些滤波器的系统函数可以通过理论分析求得。
-
低通滤波器:
系统函数为 $H(s)=\frac{\omega_{0}^{2}}{s^{2}+2\zeta\omega_{0}s+\omega_{0}^{2}}$,其中 $\omega_{0}$ 是截止频率,$\zeta$ 是阻尼比。 -
高通滤波器:
系统函数为 $H(s)=\frac{s^{2}}{s^{2}+2\zeta\omega_{0}s+\omega_{0}^{2}}$,其中 $\omega_{0}$ 是截止频率,$\zeta$ 是阻尼比。 -
带通滤波器:
系统函数为 $H(s)=\frac{\omega_{0}^{2}}{(s^{2}+\omega_{0}^{2})+s\cdot Q_{p}\cdot\omega_{0}}$,其中 $\omega_{0}$ 是中心频率,$Q_{p}$