文章目录
前言
本文只要记录一些书中的一些小知识点,挑一些本人认为重要的地方进行总结。
各位道友!道长(zhǎng) 道长(chǎng)
一、逻辑斯谛回归模型
1.1逻辑斯谛分布
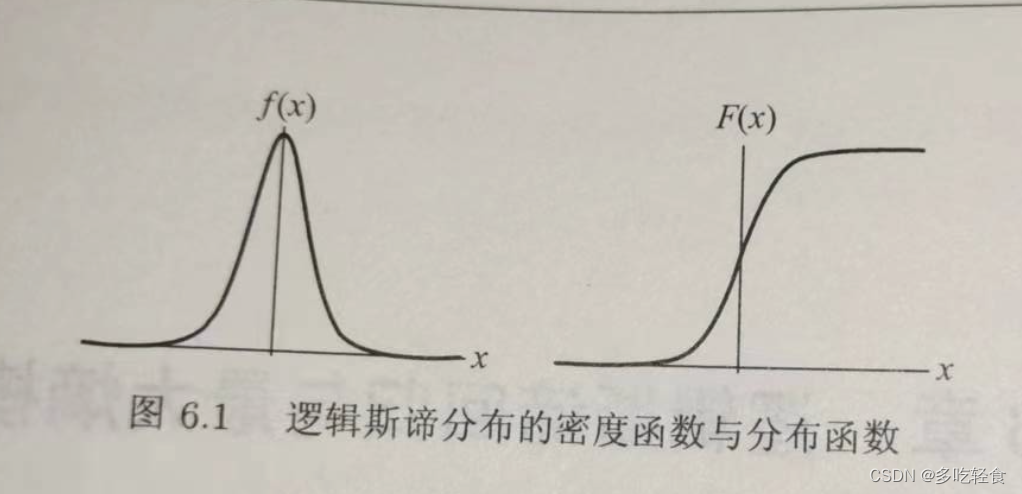
设X是连续随机变量,X服从逻辑斯谛分布指X具有下列分布函数和密度函数:
F ( x ) = P ( X ≤ x ) = 1 1 + e − ( x − μ ) / γ F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu)/ \gamma}} F(x)=P(X≤x)=1+e−(x−μ)/γ1
f ( x ) = F ′ ( x ) = e − ( x − μ ) / γ γ ( 1 + e − ( x − μ ) / γ ) 2 f(x)=F'(x)=\frac {e^{-(x-\mu)/ \gamma}}{\gamma (1+e^{-(x-\mu)/ \gamma})^2} f(x)=F′(x)=γ(1+e−(x−μ)/γ)2e−(x−μ)/γ
其中, μ \mu μ为位置参数, γ > 0 \gamma>0 γ>0为形状参数。
1.它的分布函数以 ( μ , 1 2 ) (\mu,\frac12) (μ,21)中心对称。
2.曲线在中心附近增长速度较快,两端速度较慢。
3.形状参数 γ \gamma γ越小,曲线在中心增长的越快。
图形如下:
1.2二项逻辑斯谛回归模型
这是一种分类模型,他是如下的条件概率分布:
P ( Y = 1 ∣ x ) = exp ( w ⋅ x + b ) 1 + exp ( w ⋅ x + b ) P(Y=1|x)=\frac{\exp(w·x+b)}{1+\exp (w·x+b)} P(Y=1∣x)=1+exp(w⋅x+b)exp(w⋅x+b)
P ( Y = 0 ∣ x ) = 1 1 + exp ( w ⋅ x + b ) P(Y=0|x)=\frac{1}{1+\exp (w·x+b)} P(Y=0∣x)=1+exp(w⋅x+b)1
- Y ∈ { 0 , 1 } Y\in\{0,1\} Y∈{0,1}是输出, ω ∈ R n \omega\in R^n ω∈Rn和 b ∈ R b \in R b∈R是参数
- ω \omega ω称为权值向量,b为偏置
- ω ⋅ x \omega·x ω⋅x为内积
对于给定的输入实例x,按照如上式子可以去的相应的条件概率。逻辑斯谛回归比较两个条件概率值的大小,将实例x分到概率值大的那一类。
为了方便,将权值向量和输入向量扩充。 ω = ( ω ( 1 ) , ω ( 2 ) . . . ω ( n ) , b ) T \omega=( \omega^{(1)} , \omega^{(2)} ...\omega^{(n)},b)^T ω=(ω(1),ω(2)...ω(n),b)T, x = ( x ( 1 ) , x ( 2 ) , . . . , x ( n ) , 1 ) T x={(x^{(1)},x^{(2)},...,x^{(n)},1)^T} x=(x(1),x(2),...,x(n),1)T。
这时,模型如下:
P ( Y = 1 ∣ x ) = exp ( w ⋅ x ) 1 + exp ( w ⋅ x ) P(Y=1|x)=\frac{\exp(w·x)}{1+\exp (w·x)} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)
P ( Y = 0 ∣ x ) = 1 1 + exp ( w ⋅ x ) P(Y=0|x)=\frac{1}{1+\exp (w·x)} P(Y=0∣x)=1+exp(w⋅x)1
现在考察逻辑斯谛回归模型的特点:
一个事件的几率是该事件发生的概率与不发生概率的比值。若发生概率是p,则它的几率是 p 1 − p \frac{p}{1-p} 1−pp,那么它的对数几率或logit函数是
l o g i t ( p ) = p 1 − p logit(p)=\frac{p}{1-p} logit(p)=1−pp
对于逻辑斯谛回归而言,得(将 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)带入即可得,注意这里的log其实是ln)
log P ( Y = 1 ∣ x ) 1 − P ( Y = 1 ∣ x ) = ω ⋅ x \log \frac{P(Y=1|x)}{1-P(Y=1|x)}=\omega \cdot x log1−P(Y=1∣x)P(Y=1∣x)=ω⋅x
也就是说,输出Y=1的对数几率是x的线性函数。或者说输出Y=1的对数几率是由输入x的线性函数表示的模型,积逻辑斯蒂回归模型。
换一个角度,考虑对输入x进行分类的的线性函数 ω ⋅ x \omega \cdot x ω⋅x,其值域是实数域。通过逻辑斯蒂定义式 P ( Y = 1 ∣ x ) P(Y=1|x) P(Y=1∣x)可以将线性函数 ω ⋅ x \omega \cdot x ω⋅x转换成概率
( Y = 1 ∣ x ) = exp ( w ⋅ x ) 1 + exp ( w ⋅ x ) (Y=1|x)=\frac{\exp(w·x)}{1+\exp (w·x)} (Y=1∣x)=1+exp(w⋅x)exp(w⋅x)
这时,
- 线性函数的值越接近正无穷,概率值越接近1。
- 线性函数越接近负无穷,概率值越接近0。
即之前的图像所示。
1.3 模型的参数估计
对于给定的训练集合 T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),...,(x_N,y_N) \} T={(x1,y1),...,(xN,yN)}, y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1}
可以应用极大似然估计法估计模型参数,得到逻辑斯谛模型。
首先设两个概率:
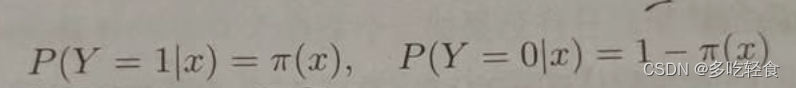
故他们的似然函数为:
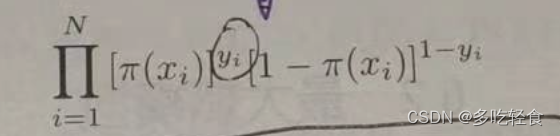
对数似然函数为
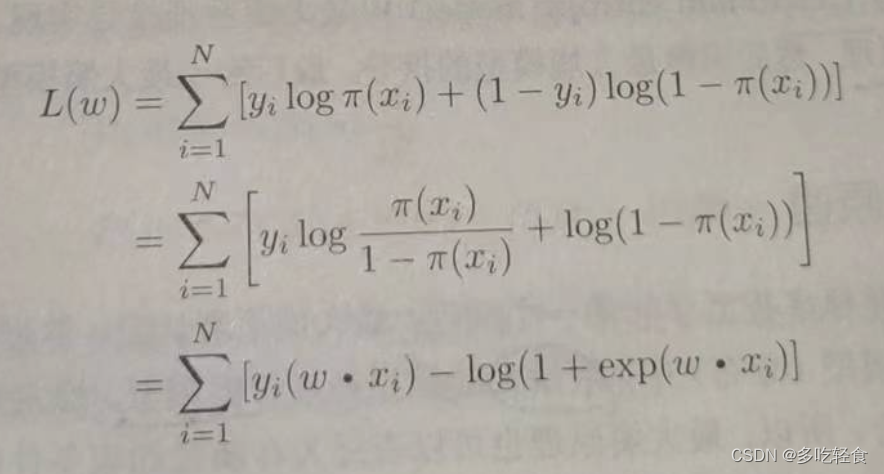
对 L ( ω ) L(\omega) L(ω)求极大值,得到 ω \omega ω的估计值。
这样问题就变成了以对数似然函数为目标函数的最优化问题。通常采用梯度下降法和拟牛顿法进行目标函数的最优化。
假设 ω \omega ω的极大似然估计值是 ω ^ \hat\omega ω^,那么逻辑斯蒂回归模型为
P ( Y = 1 ∣ x ) = exp ( w ^ ⋅ x ) 1 + exp ( w ^ ⋅ x ) P(Y=1|x)=\frac{\exp(\hat w·x)}{1+\exp (\hat w·x)} P(Y=1∣x)=1+exp(w^⋅x)exp(w^⋅x)
P ( Y = 0 ∣ x ) = 1 1 + exp ( w ^ ⋅ x ) P(Y=0|x)=\frac{1}{1+\exp (\hat w·x)} P(Y=0∣x)=1+exp(w^⋅x)1
1.4 多项逻辑斯谛回归
P ( Y = k ∣ x ) = exp ( w k ⋅ x ) 1 + ∑ k = 1 K − 1 exp ( w k ⋅ x ) P(Y=k|x)=\frac{\exp( w_k·x)}{1+\sum_{k=1}^{K-1}\exp ( w_k·x)} P(Y=k∣x)=1+∑k=1K−1exp(wk⋅x)exp(wk⋅x)
P ( Y = K ∣ x ) = 1 1 + ∑ k = 1 K − 1 exp ( w ⋅ x ) P(Y=K|x)=\frac{1}{1+\sum_{k=1}^{K-1}\exp ( w·x)} P(Y=K∣x)=1+∑k=1K−1exp(w⋅x)1
二、最大熵模型
2.1 最大熵原理
最大熵原理认为,所有可能的概率模型中,熵最大的模型是最好的模型。最大熵原理认为要选择的概率模型首先必须满足已有的事实(约束条件)。没有更多信息的情况下,那些不确定的部分都是“等可能的”
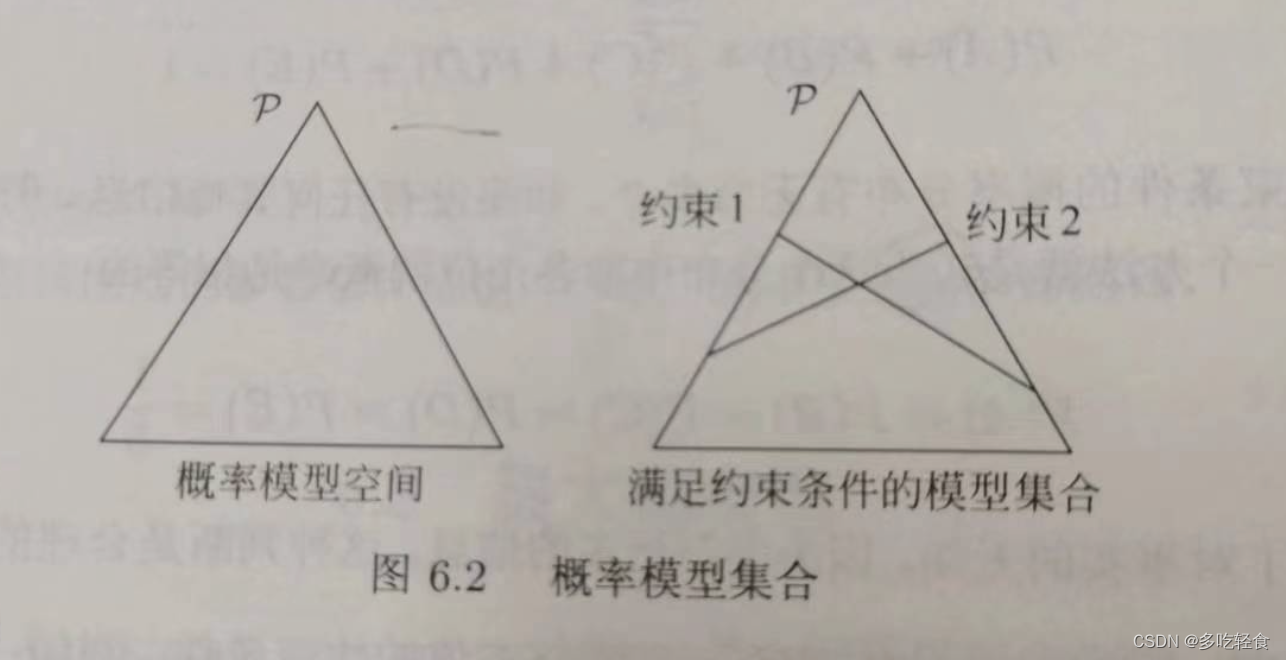
2.2定义
假设满足所有约束条件的模型集合为
C = { P ∈ P 1 ∣ E P ( f i ) = E P ~ ( f i ) } C=\{P \in P1|E_P(f_i)=E_{\tilde{P}}(f_i) \} C={P∈P1∣EP(fi)=EP~(fi)}
定义在条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)上的条件熵为(如无说明,一般log都是ln)
H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) H(P)=-\sum_{x,y}\tilde{P}(x)P(y|x)\log P(y|x) H(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
2.3最大熵模型的学习
对于给定数据集 T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),...,(x_N,y_N)\} T={(x1,y1),...,(xN,yN)}和特征函数 f i ( x , y ) , i = 1 , 2... , n f_i(x,y),i=1,2...,n fi(x,y),i=1,2...,n,最大熵模型的学习等价于约束最优化问题
max P ∈ C H ( P ) = − ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) \max_{P\in C}H(P)=-\sum_{x,y} \tilde{P}(x) P(y|x) \log P(y|x) P∈CmaxH(P)=−x,y∑P~(x)P(y∣x)logP(y∣x)
s . t . E P ( f i ) − E P ~ ( f i ) = 0 , i = 1 , 2 , . . . , n s.t.\quad E_P(f_i)-E_{\tilde{P}}(f_i)=0 ,\quad i=1,2,...,n s.t.EP(fi)−EP~(fi)=0,i=1,2,...,n
∑ y P ( y ∣ x ) = 1 \sum_{y}P(y|x)=1 y∑P(y∣x)=1
- 这里n为特征函数f的个数
按照习惯,将问题改写为等价的最小值问题
max P ∈ C − H ( P ) = ∑ x , y P ~ ( x ) P ( y ∣ x ) log P ( y ∣ x ) \max_{P\in C} -H(P)=\sum_{x,y} \tilde{P}(x) P(y|x) \log P(y|x) P∈Cmax−H(P)=x,y∑P~(x)P(y∣x)logP(y∣x)
s . t . E P ( f i ) − E P ~ ( f i ) = 0 , i = 1 , 2 , . . . , n s.t.\quad E_P(f_i)-E_{\tilde{P}}(f_i)=0 ,\quad i=1,2,...,n s.t.EP(fi)−EP~(fi)=0,i=1,2,...,n
∑ y P ( y ∣ x ) = 1 \sum_{y}P(y|x)=1 y∑P(y∣x)=1
这里将约束最优化问题转换为无约束最优化问题的对偶问题。
首先引入拉格朗日乘子 w 0 , . . . , w n w_0,...,w_n w0,...,wn,定义拉格朗日函数
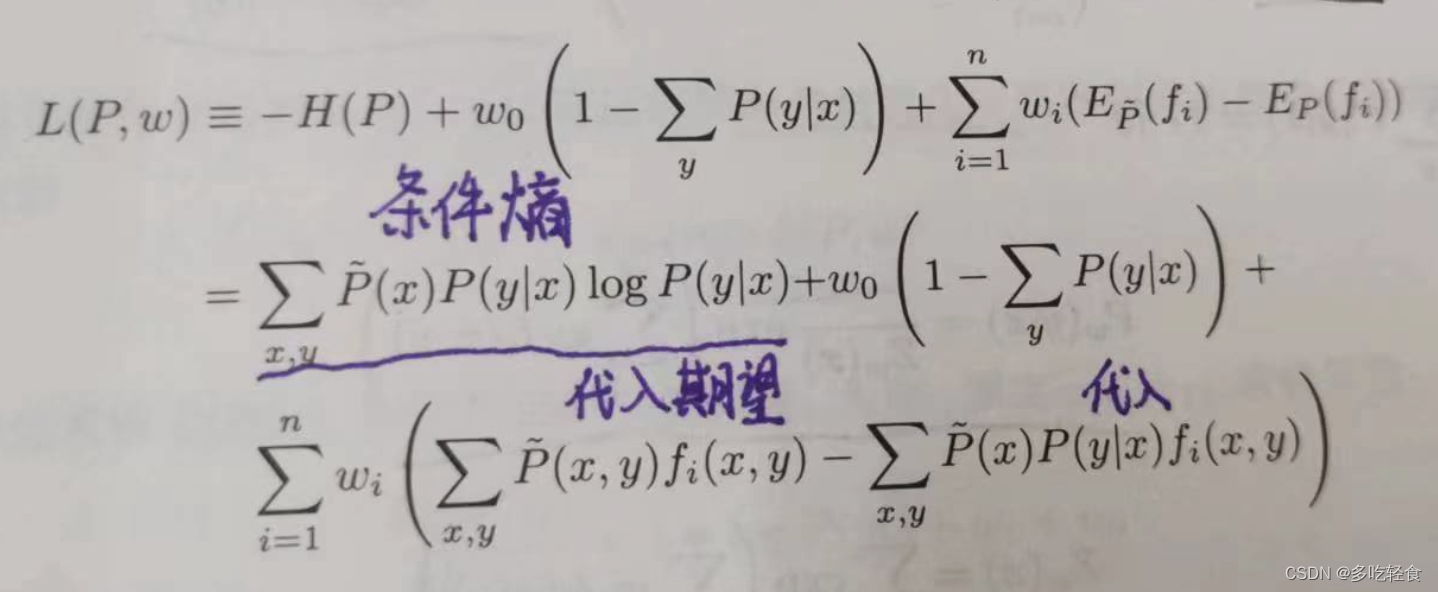
这里,对于两个期望的值
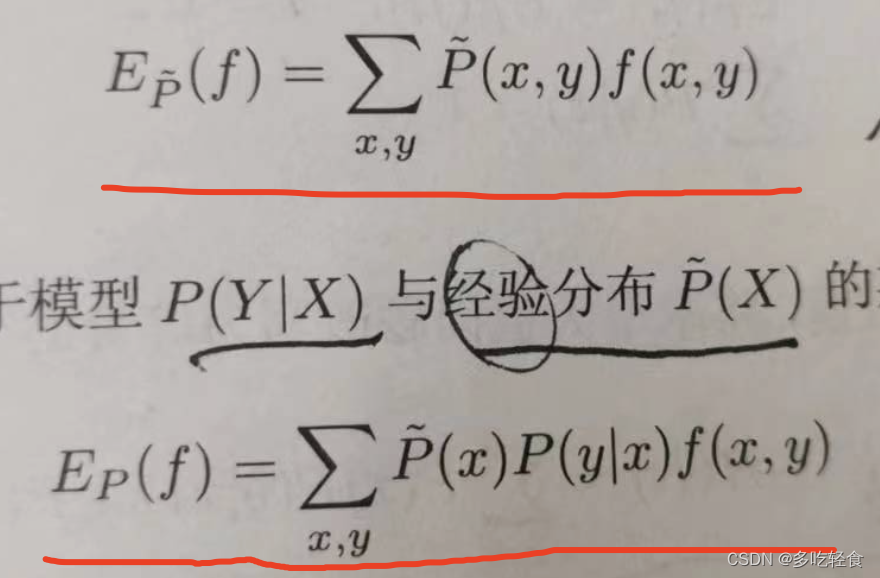
原始问题为
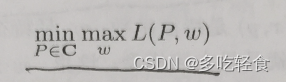
对偶问题是

由于该拉格朗日函数是关于P的凸函数,所以原始问题与对偶问题的解是等价的。
继续。
首先 min p ∈ C L ( P , w ) \min_{p\in C}L(P,w) minp∈CL(P,w)是关于 w w w的函数(因为P是通过arg最小优化得到,然后w变成了可以移动的变量),记作:
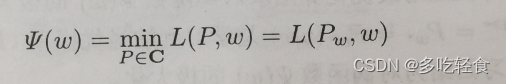
将P的解记作
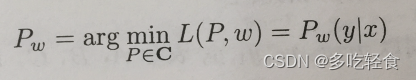
用拉格朗日法对P(y|x)求偏导数 
令这个偏导数为0,也就是绿色部分等于0

得P(y|x)
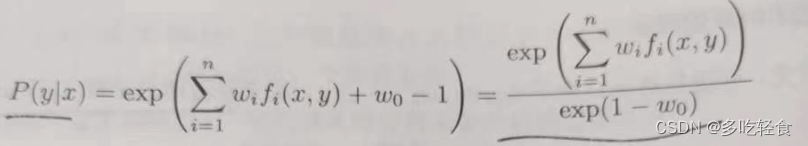
然后,
由条件概率的特性
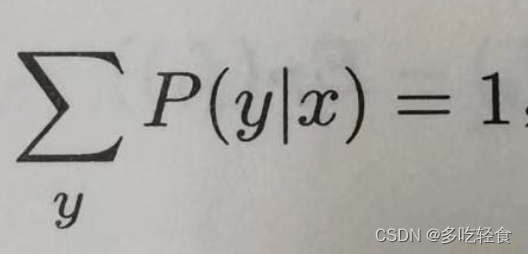
即
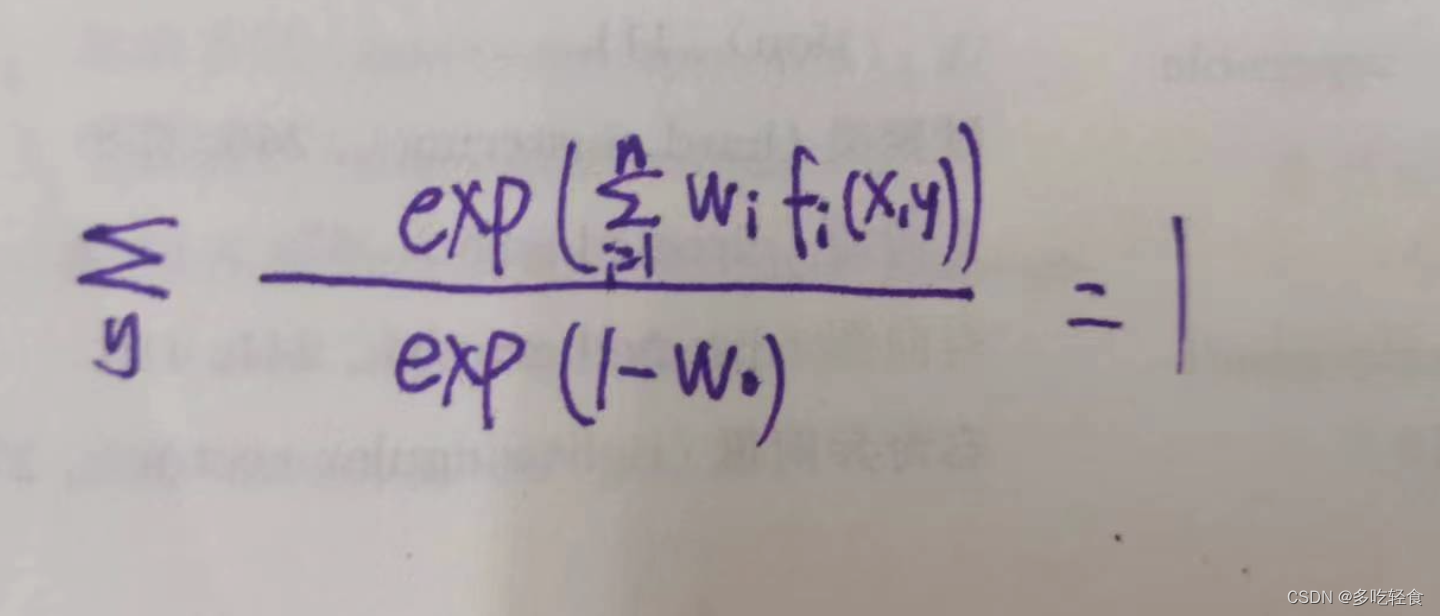
因为分母不受y的影响,所以分母都相等,把求和符号放上面

然后令 Z w Z_w Zw等于
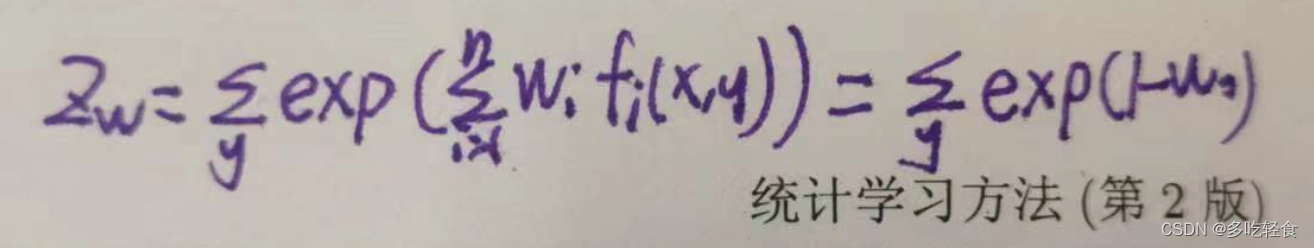
最终有最大熵模型 P w = P w ( y ∣ x ) P_w=P_w(y|x) Pw=Pw(y∣x):
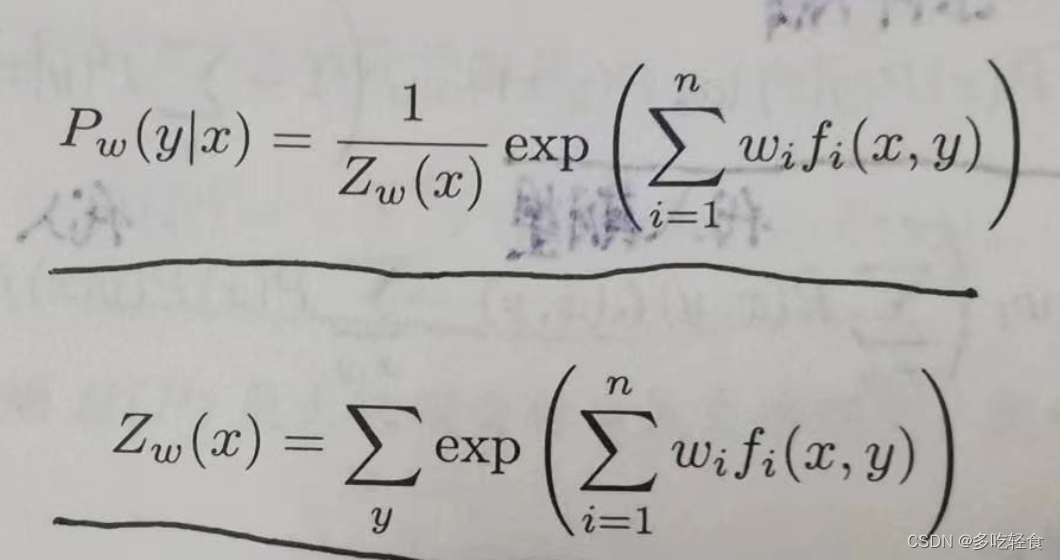
最后对对偶问题极大化,并记它的解为 w ∗ w^* w∗: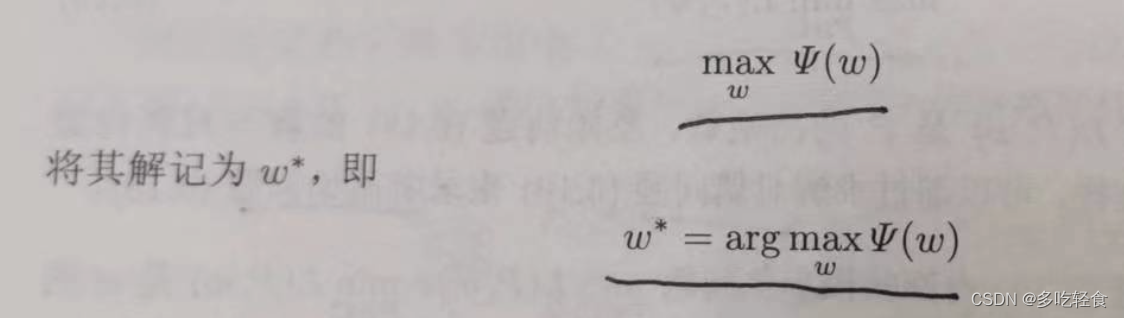
2.4极大似然估计
上面讲的对偶函数的极大化等驾驭最大熵模型的极大似然估计。
证明在书上。


2.5模型学习的最优化算法
1.改进的迭代尺度法IIS
想法:
假设最大熵模型的参数向量是 w = ( w 1 , w 2 , . . . , w n ) T w=(w_1,w_2,...,w_n)^T w=(w1,w2,...,wn)T,我们希望找到一个新的参数向量 w + δ w+\delta w+δ使得模型的对数似然估计增大。然后一直重复 w → w + δ w \rightarrow w+\delta w→w+δ,直到找到对数似然函数的最大值。
算法如下:

- 注意:这里关键是(a)步。
- 如果 f # = M f^{\#}=M f#=M, δ i = 1 M log E P ~ ( f i ) E p ( f i ) \delta_i=\frac{1}{M}\log \frac{E_{\tilde{P}(f_i)}}{E_p(f_i)} δi=M1logEp(fi)EP~(fi)
- 如果 f # f^{\#} f#不是常数,需要牛顿法计算 δ i \delta_i δi,迭代公式为
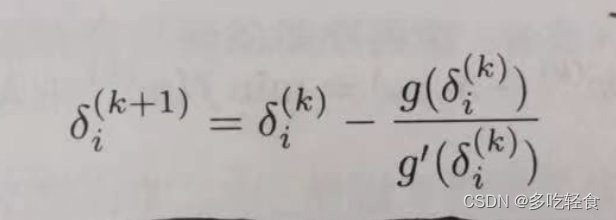
总结
今天的内容是统计学习方法的第六章节,逻辑斯蒂回归和最大熵模型大多是用于多类分类,是判别模型。机器学习中有一个典型的s型激活函数中就有一个逻辑斯谛函数。
最近在读汪曾祺的《人间草木》,写的东西可太美了。
汪先生在短篇《夏天》中写道:“夏天的早晨很舒服。空气很凉爽,草上还挂着露水,写大字一张,读古文一篇。夏天的早晨真舒服。”
夏天到了,希望大家也要享受这个夏天呀!