外观说明

Q0系列CPU模块说明书ATCIQ02232.pdf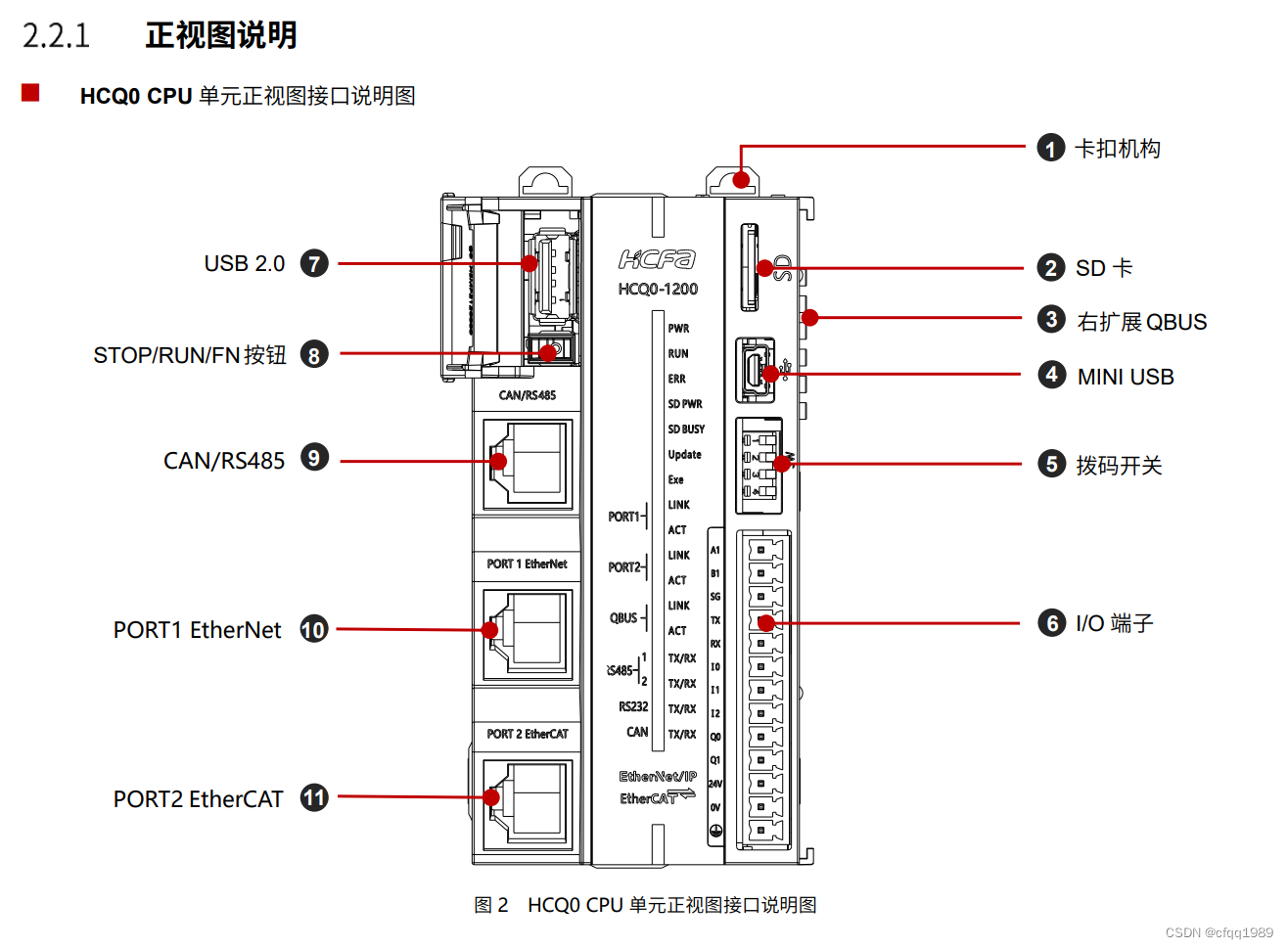

千兆以太网口支持 Modbus TCP ；  选择》 简单模式

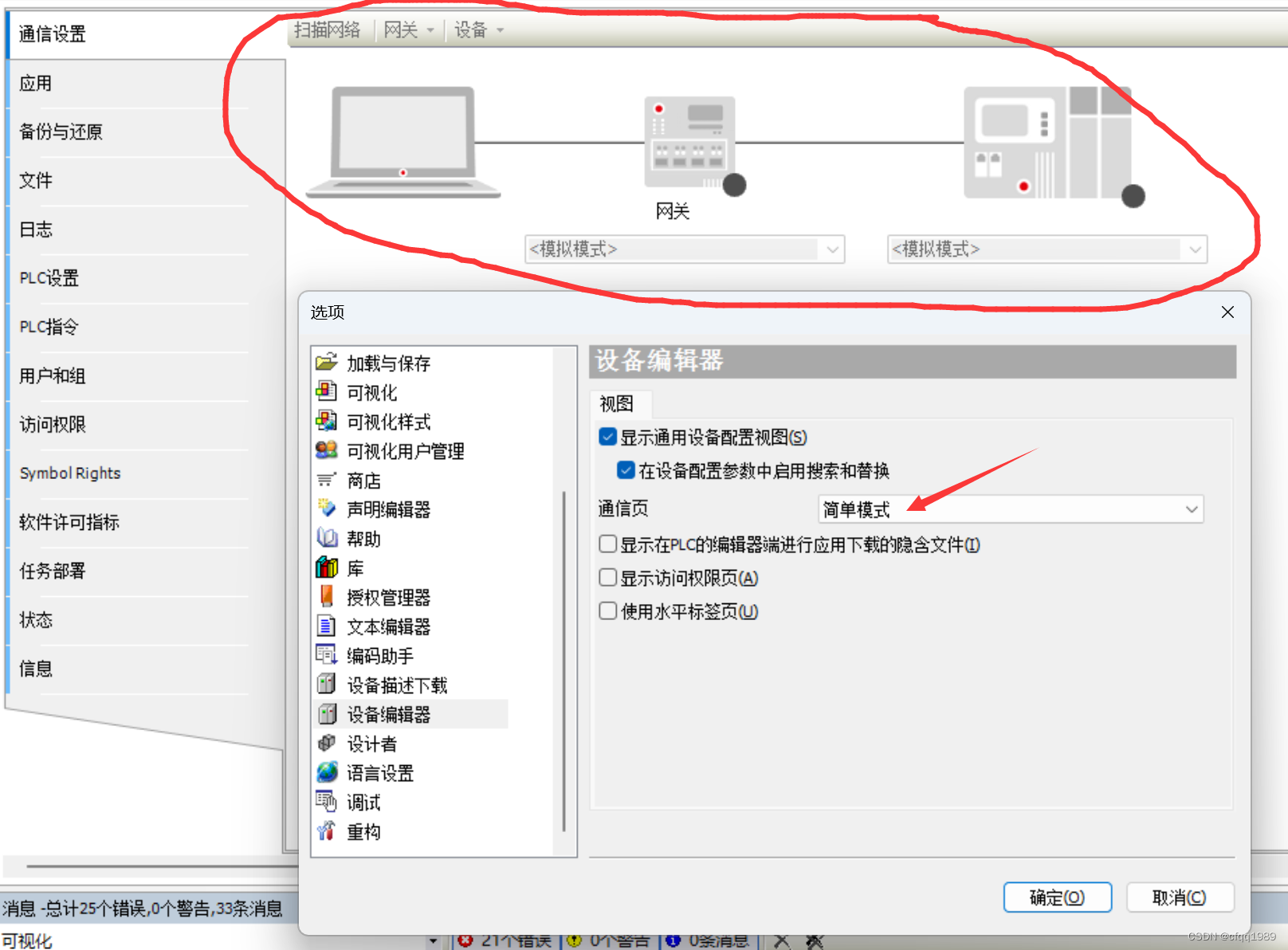
IPV4：192.168.88.100 子网掩码：255.255.255.0  

 FN功能

。长按 FN 是指将开关拨到 FN 并维持 2S 以上。完成后重启

 

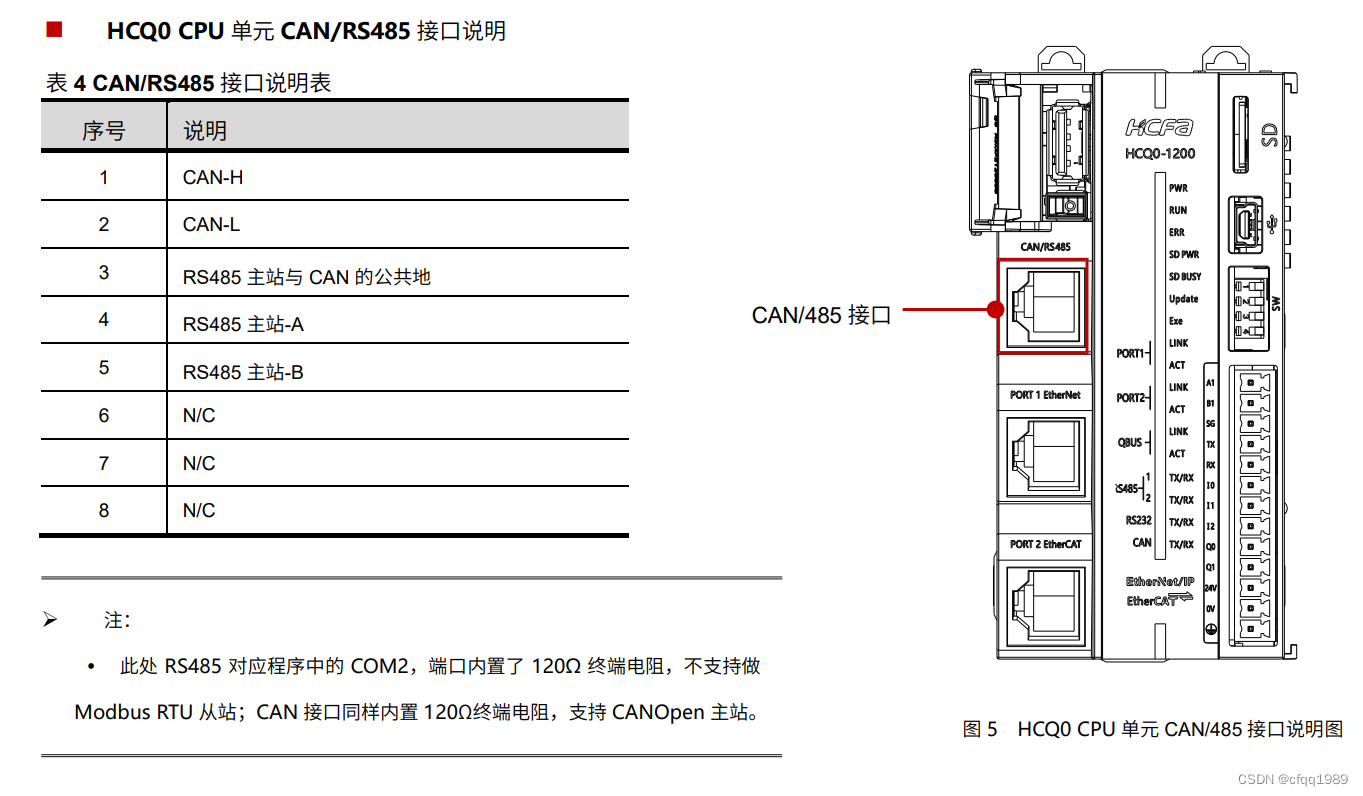
程序总容量    16MBytes
I区(%)           128kBytes
Q区(%Q)          128kBytes
编程
M区 (%M)         512kBytes
掉电保持区       800kBytesCPU 16bit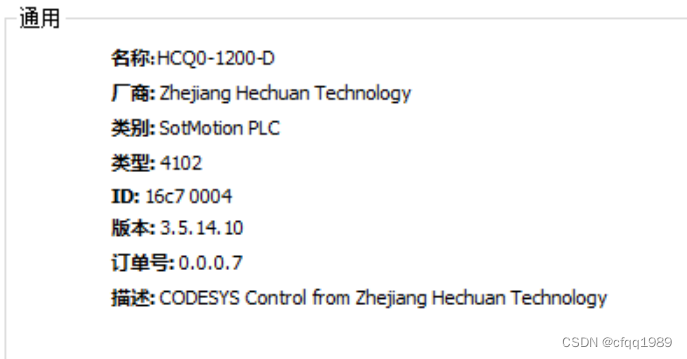

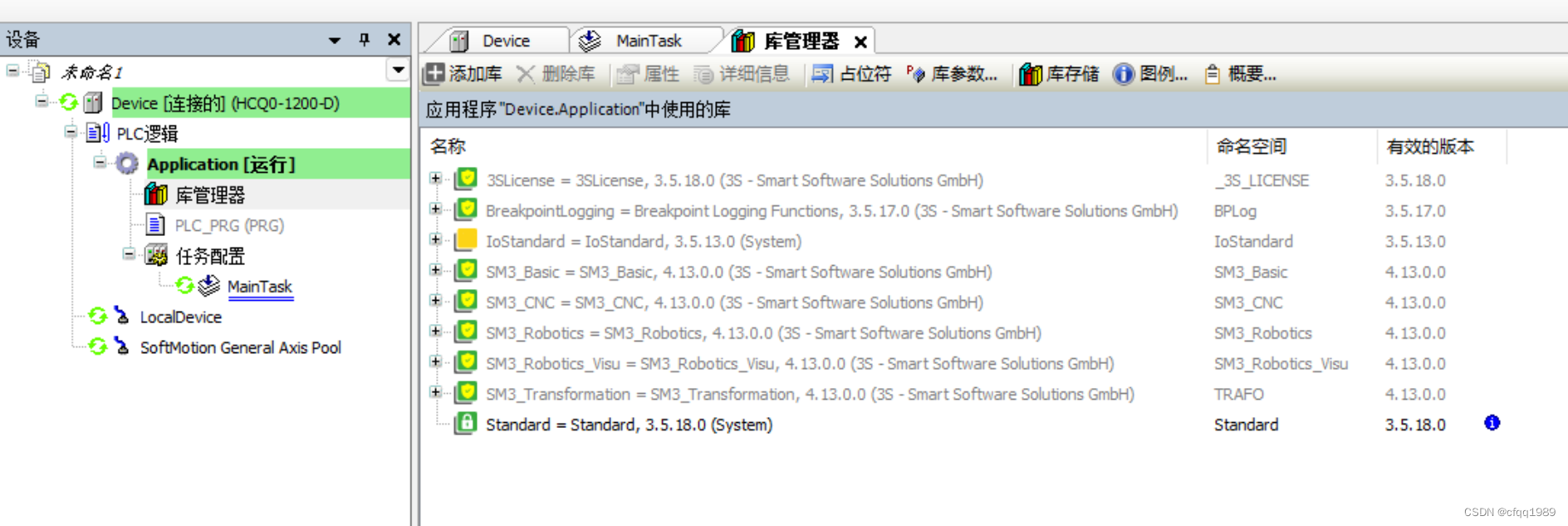
编译不报错，下载就报错：

库版本的问题导致的，需要降级库版本（占位符）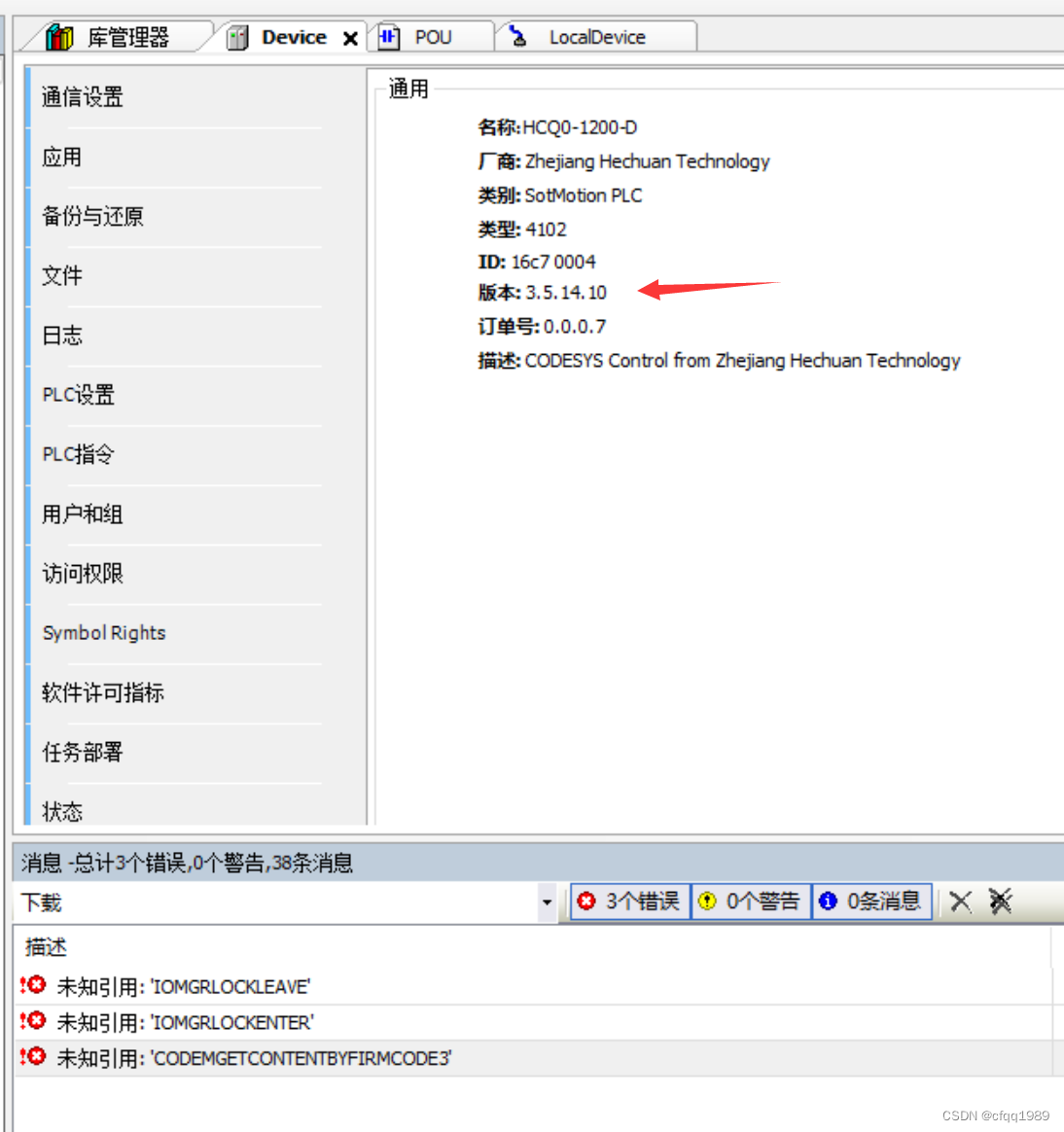

 

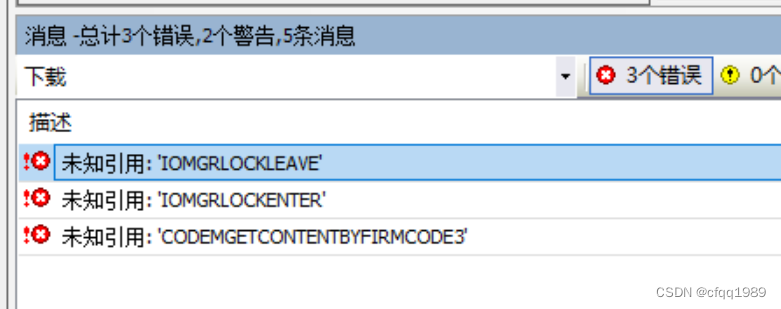
 固件版本是：  3.5.14     需要注意软件库版本尽量不要超过这个。

有些版本，不能超过固件版本
cmpCodeMeter
ioStandard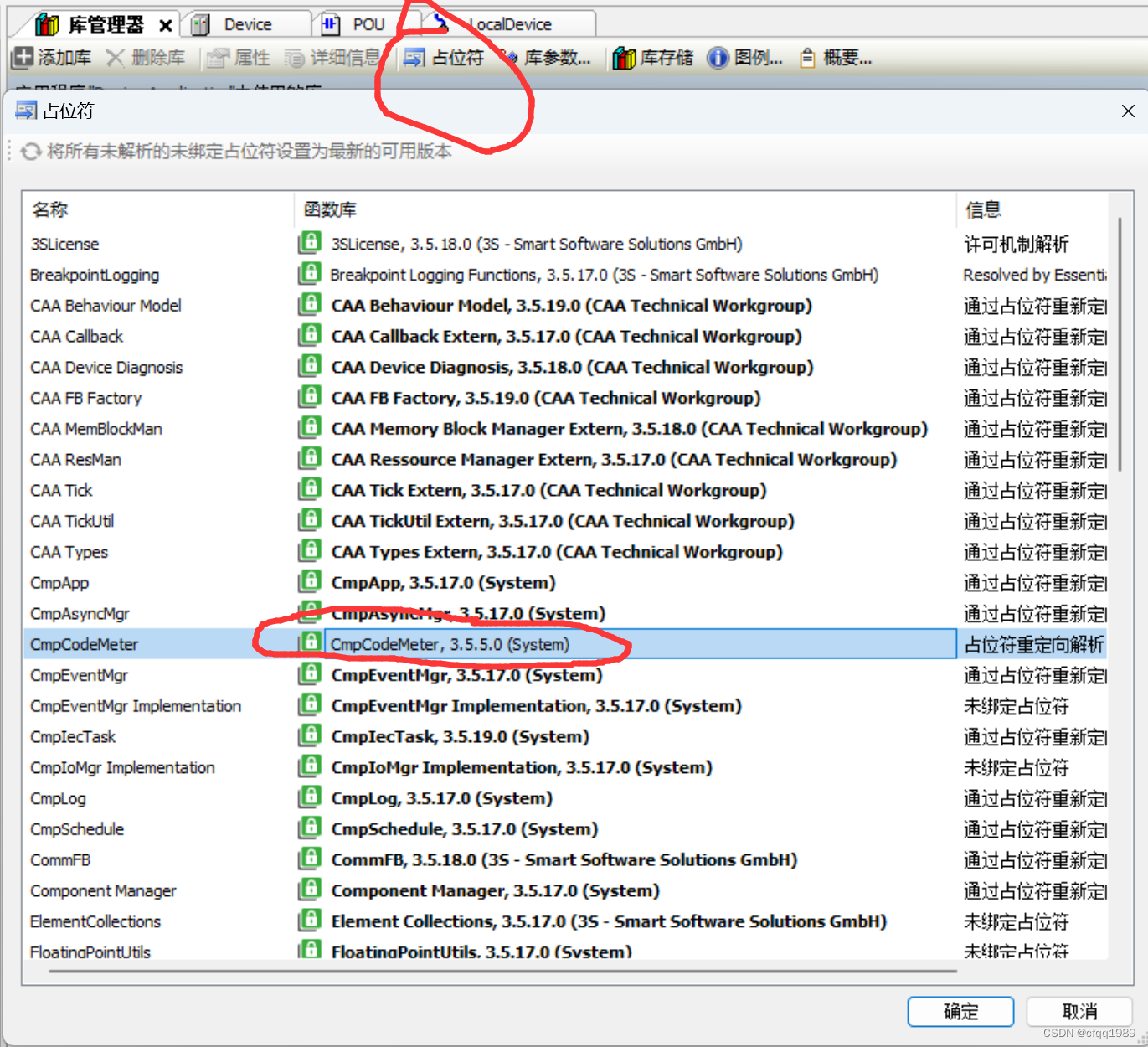

 

 利用错误关键字，在库里找出这个是属于哪方面的，做降级参考。

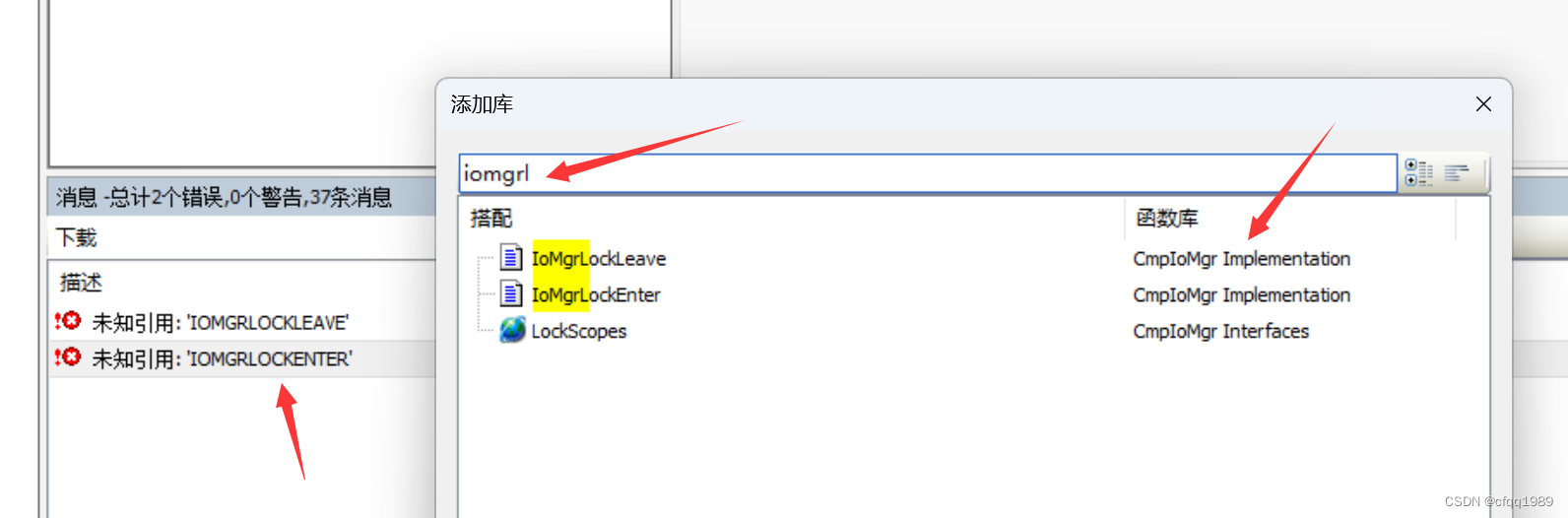
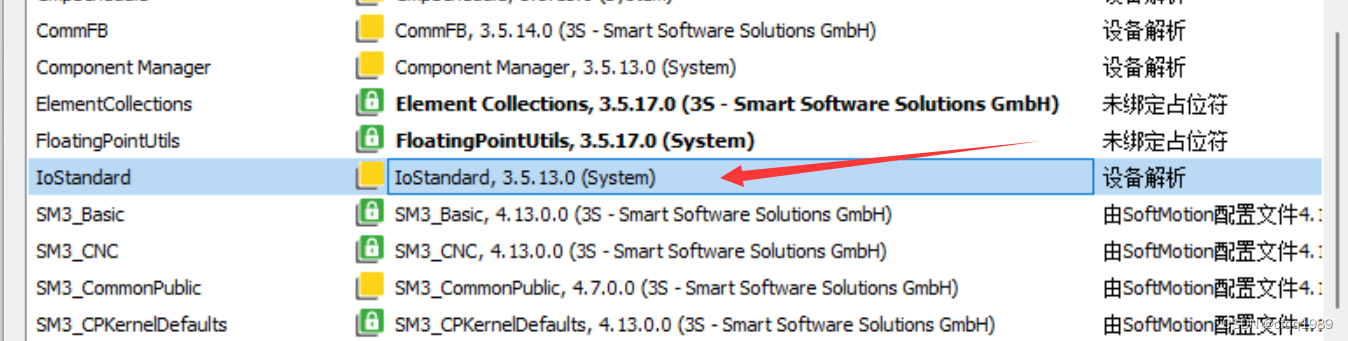
 降级这2个库后，程序下载到PLC就不报错了。

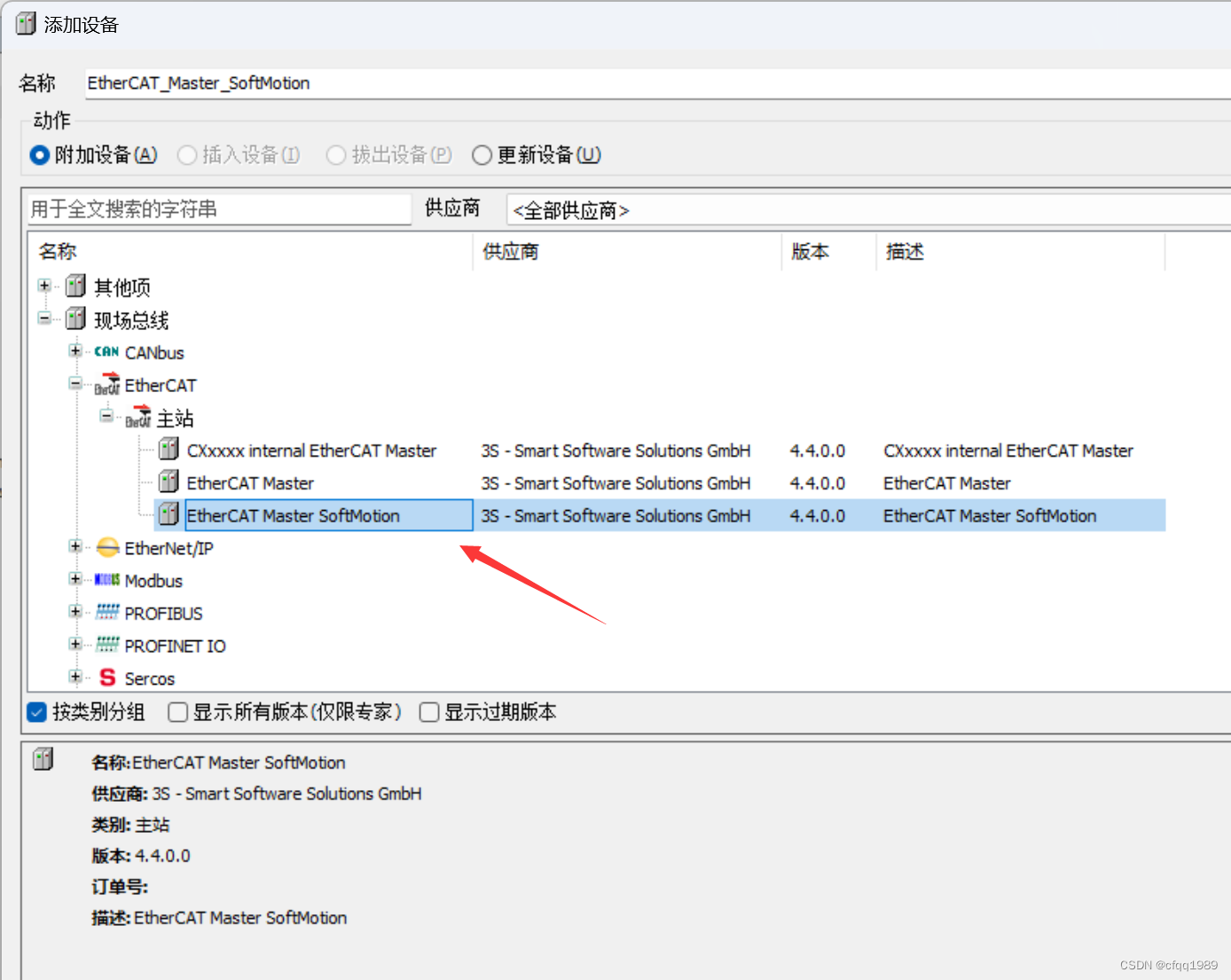
添加can总线： 

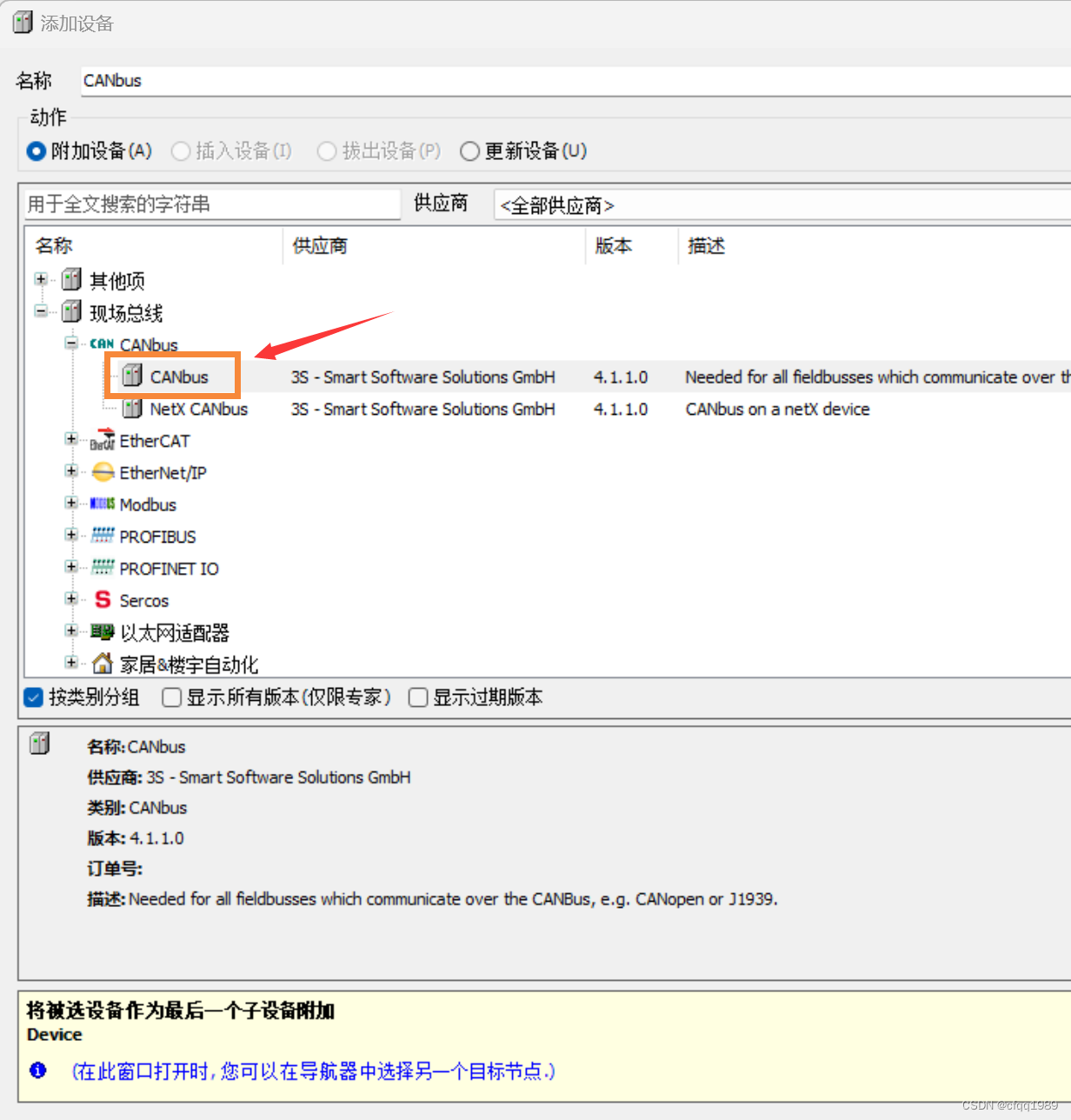
 在can模块下，再添加can主站

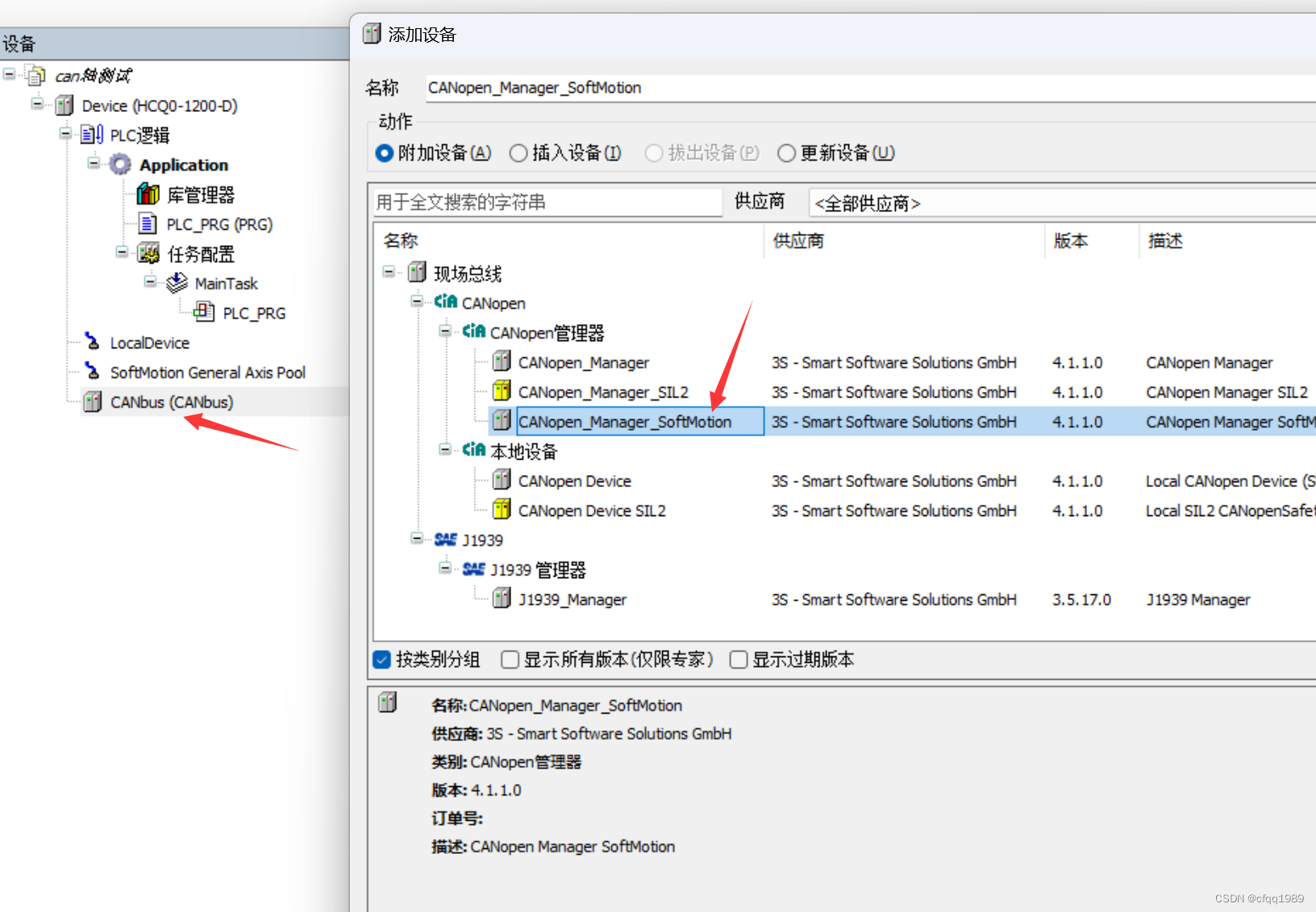
 右键》添加设备

添加can库：

说明文档：  禾川Q系列CANOPEN应用教程V1.3-20210907.pdf库函数文件：  库函数HCFA_CANopenLib_0.0.0.4.compiled-library注意：库函数文件，官网上下载不了，只能人工服务，问客服索取。

ECAT主站添加：