目录
1.概述
RSA%E6%B5%8B%E8%AF%95-toc" style="margin-left:0px;">2. RSA测试
2.1 加解密实验
2.2 签名验签测试
RSA%E5%8E%9F%E7%90%86%E7%AE%80%E4%BB%8B%C2%A0-toc" style="margin-left:0px;">3. RSA原理简介
4.小结
1.概述
从上面密码学基础 -- 走进RSA(1)(放弃数学原理版)-CSDN博客我们知道了非对称算法的密钥对使用时机,那么接下里我们继续讲解RSA,我们分别从RSA加解密、签名验签以及其原理概述入手
RSA%E6%B5%8B%E8%AF%95">2. RSA测试
我们从一个具体的RSA签名试验开始认识其原理。 在之前文章,我们已经生成了基于RSA的密钥对,格式如下:
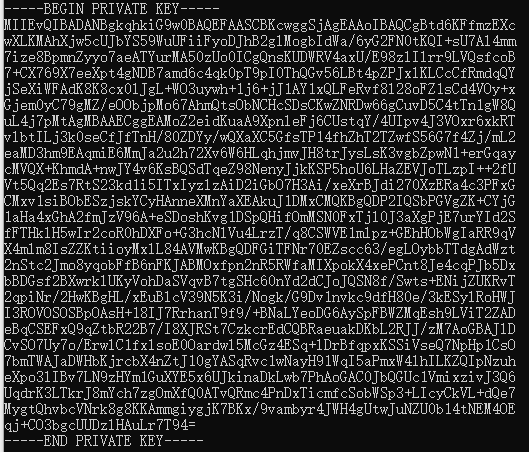

但是这一堆乱码简直没办法分析,所以我们通过openssl将密钥对hex数据打印出来,如下:
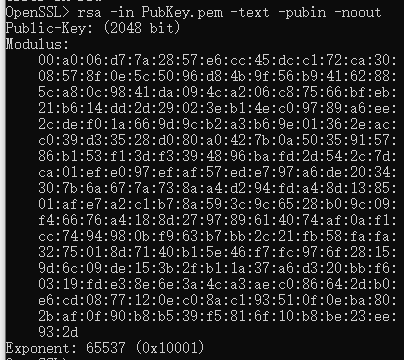
公钥Hex数据
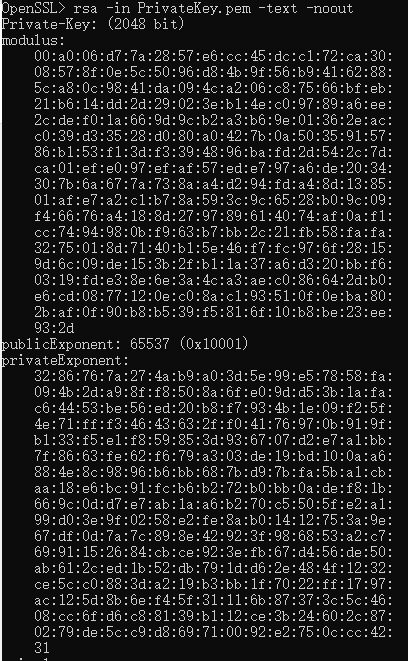

私钥Hex数据
公钥里包含了模数(Modulus)、指数(Exponent);
私钥包含了模数(Modulus)、私钥指数(privateExponent)、公钥指数(publicExponent)、prime(质数)1\2、exponent(指数)1\2、系数(coefficient).
根据RFC8017定义,并结合示例,可以总结公私钥的构成如下:

2.1 加解密实验
首先使用openssl对demo.txt进行加密,生成密文文件demo.en,如下:

然后使用私钥进行解密,得到demo_enc.txt,如下:

2.2 签名验签测试
首先使用openssl对文档signDemo.txt进行签名,得到签名hex,如下:
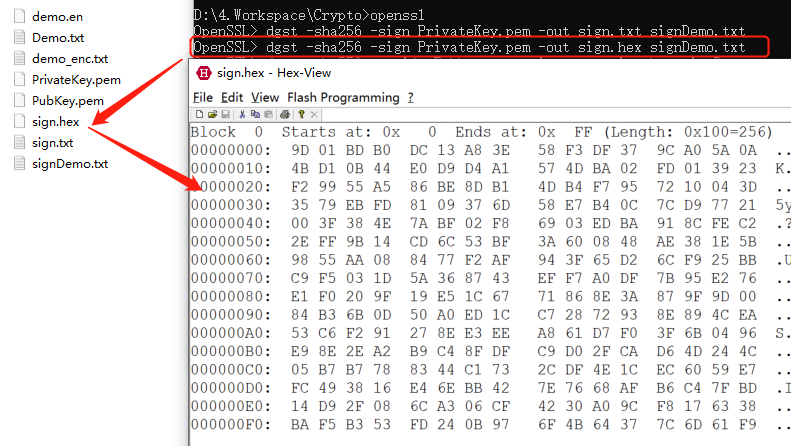
然后进行验签,得到验签结果,如下:
![]()
RSA%E5%8E%9F%E7%90%86%E7%AE%80%E4%BB%8B%C2%A0">3. RSA原理简介
有了上述测试,我们对RSA有了感性认识,接下来就讲点纯理论的东西。
RSA是由麻省理工的Rivest、Shamir和Adleman在1978年提出,其数学基础用到了欧拉定理,安全性由大因子分解十分困难保证,利用了单向陷门函数的原理,具体如下:
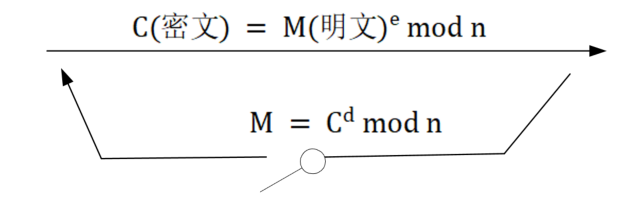
其中{e,n}表示公钥,{d,n}表示私钥。
该算法安全在哪里呢?在于私钥难以被破解。
该算法生成密钥的过程如下:
- 选择两个大素数p和q(通常要求每个素数均大于10的100次方)
- 计算一个 n = p * q ,φ(n) = (p-1)*(q-1)
- 在(1,φ(n))之间找到一个整数e,该数与φ(n)互质;e作为公钥
- 根据e和φ(n)计算出私钥d,必须满足 e*d mod φ(n) = 1;密钥对 {{e,n} , {d,n}}
- 将明文划分成块,记为m,保证每个明文的长度 len(m) < n
- 加密过程:c = m^e mod n (加密需要公钥e 和 n)
- 解密过程:m = c^d mod n (解密需要私钥d 和 n)
以上述为例:攻击者可以容易获取到的数据有密文c、模数n和公钥e,几乎不能获取私钥d; 解密需要私钥d,d是根据e和φ(n)计算得来,n有p和q计算得出 因此需要对n进行因子分解,找出两个素数p和q 例如 21,很容易得出两个素数3 和7,但如果n为2048bit的整数,目前从数学角度难解决。
4.小结
上面文章,我们讲述了非对称算法的加解密、签名验签的原理,并做了相关测试工作;从数学角度讲述了RSA密钥生成原理,并且详细阐述了RSA中每个字母的含义。
这对基于硬件密码加速引擎实现非对称算法具有非常强的参考意义。
一般来讲,HSM所能提供的非对称算法的硬件加速功能通常只包含数学运算,例如加减乘除、模数运算等等,我们要实现RSAES、RSASSA、ECDSA等算法,是需要利用这些运算加速来实现公式的,举个例子,假设要实现RSA签名工作,首先需要调用Hash加速器来生成摘要,然后通过调用模幂运算来对摘要进行加密,这就需要我们理解模数、指数应该分别放到指定的寄存器里以供非对称引擎调用。