自动驾驶---Control之LQR控制

1 前言

在前面的系列博客文章中为读者阐述了很多规划相关的知识（可参考下面专栏），本篇博客带领读者朋友们了解控制相关的知识，后续仍会撰写规控相关文档。

在控制理论的发展过程中，人们逐渐认识到对于线性动态系统的控制，可以通过优化某种性能指标来达到更好的控制效果。而LQR控制就是基于这种思想发展而来的。它通过将系统状态与控制信号之间的关系表示成一种二次型，然后通过最小化这个二次型来求解最优的控制策略。

目前的工业领域三大控制器占据着主要位置：PID，LQR以及MPC，本篇博客为读者介绍LQR控制器。

2 LQR建模求解

LQR（Linear quadratic regulator，线性二次型调节器）是一种基于状态反馈的最优控制策略，其核心在于设计一个状态反馈控制器，使得系统的性能指标达到最优。下面将对LQR控制器进行详细介绍：

2.1 原理与步骤

确定状态方程模型：首先需要确定一个描述系统状态的动力学模型，该模型通常以状态空间的形式给出，用于描述系统在不同状态下的动态行为。
线性化处理：对状态方程进行线性化处理，将其转化为线性系统模型。这是为了简化问题，使得控制器设计更加便捷。
定义目标函数：目标函数通常是系统状态和控制输入的二次型函数，用于评估控制性能的好坏。这个函数的选择会直接影响到控制器的设计效果。
优化目标函数：通过设计状态反馈控制器，使得目标函数取最小值。这个过程中，需要求解一个最优控制问题，通常涉及到Riccati方程的求解。

2.2 详细内容

2.2.1 一般推导

对于一个闭环系统，状态方程为：

$eq?%5Cdot%7Bx%7D%3DAx+Bu$

其中 $eq?x$ 为状态量， $eq?u$ 为控制量， $eq?A%2CB$ 分别为状态矩阵，控制矩阵。假设 $eq?u%3D-Kx$ ，那么上式可以整理为一个新的状态方程：

$eq?%5Cdot%7Bx%7D%3D%28A-BK%29x%3DA_cx$

为了能够选出最优化的特征值，引入了一个代价函数，考虑两个方面的内容：

希望系统达到稳定状态使得偏差最小：惩罚状态量
希望控制量较小的情况下也能达到稳定状态：惩罚控制量

因此代价函数可以写成如下形式：

$eq?J%3D0.5*%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%28x%5ETQx+u%5ETRu%29dt$

其中， $eq?x$ 为状态量， $eq?u$ 为控制量， $eq?Q%2CR$ 分别为状态权重矩阵，控制权重矩阵。在量产中的调参也主要集中在 $eq?Q%2CR$ 矩阵上。

基于上面两个方面的考虑，这里希望 $eq?Q$ 为半正定矩阵来保证 $eq?x%5ETQx%5Cgeq%200$ ；希望 $eq?R$ 为正定矩阵来保证 $eq?u%5ETRu%3E%200$ ，该项表示控制所付出的代价。

将 $eq?u%3D-Kx$ 代入到代价函数种可得，

$eq?J%3D0.5*%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%28x%5ETQx+u%5ETRu%29dt%3D%5C%5C0.5*%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%28x%5ETQx+%28-Kx%29%5ETR%28-Kx%29%29dt%3D%5C%5C0.5*%5Cint_%7B0%7D%5E%7B%5Cinfty%7D%28x%5ETQx+x%5ETK%5ETRKx%29dt%3D%5C%5C0.5*%5Cint_%7B0%7D%5E%7B%5Cinfty%7Dx%5ET%28Q+K%5ETRK%29xdt$

为了得到 $eq?K$ 矩阵，假设存在一个常量矩阵 $eq?P$ 使得,

$eq?%5Cfrac%7B%5Cmathrm%7Bd%7D%20%7D%7B%5Cmathrm%7Bd%7D%20t%7D%28x%5ETPx%29%3D-x%5ET%28Q+K%5ETRK%29x$

将上式左边微分展开得到，并代入 $eq?%5Cdot%7Bx%7D%3DA_cx$ ，

$eq?%5Cdot%7Bx%7D%5ETPx+x%5ETP%5Cdot%7Bx%7D%3D-x%5ET%28Q+K%5ETRK%29x%5C%5C%5C%5C%20%5Cdot%7Bx%7D%5ETPx+x%5ETP%5Cdot%7Bx%7D+x%5ET%28Q+K%5ETRK%29x%3D0%5C%5C%5C%5C%20%28A_cx%29%5ETPx+x%5ETP%28A_cx%29+x%5ET%28Q+K%5ETRK%29x%3D0%5C%5C%5C%5C%20x%5ET%28A%5ET_cP+PA_c+Q+K%5ETRK%29x%3D0$

由二次型的性质可得，如果保证上式为0，则括号内的值必须为0，即：

$eq?A%5ET_cP+PA_c+Q+K%5ETRK%3D0%5C%5C%5C%5C%20%28A-BK%29%5ETP+P%28A-BK%29+Q+K%5ETRK%3D0$

上式中含有 $eq?K$ 矩阵的二次型，不利于计算，因此取 $eq?K%3DR%5E%7B-1%7DB%5ETP$ 消掉二次项得，

$eq?%28A-BK%29%5ETP+P%28A-BK%29+Q+K%5ETRK%3D0%5C%5C%5C%5C%20A%5ETP+PA+Q-K%5ETB%5ETP-PBK+K%5ETRK%3D0%5C%5C%5C%5C%20A%5ETP+PA+Q-%28R%5E%7B-1%7DB%5ETP%29%5ETB%5ETP-PB%28R%5E%7B-1%7DB%5ETP%29+%28R%5E%7B-1%7DB%5ETP%29%5ETR%28R%5E%7B-1%7DB%5ETP%29%3D0%5C%5C%5C%5CA%5ETP+PA+Q-PBR%5E%7B-1%7DB%5ETP%3D0$

从上面的公式中，可以看到形式正好是控制理论中的Riccati方程。

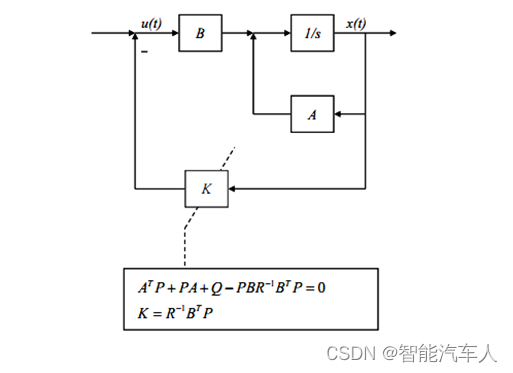
2.2.2 离散域推导

网上看到很多文章的推导结果不太一致，在此处说明，另一种形式的Riccati方程是基于离散时域的推导结果：

$eq?P%20%3D%20A%5ETPA%20-%20A%5ETPB%28R%20+%20B%5ETPB%29%5E%7B-1%7DB%5ETPA%20+%20Q$

记 $eq?t$ 时刻代价函数为 $eq?V_t$ ，价值函数为 $eq?Q_t$ ，其中 $eq?%5Bt%3DN%2CN-1...1%2C0%5D$

$eq?V_t%28x_t%29%3Dmin_%7Bu_t%7Dx%5ET_tQx_t+u%5ET_tRu_t+V_%7Bt+1%7D%28x_%7Bt+1%7D%29%2C%20t%3C%3DN-1%5C%5C%5C%5C%20V_N%28x_N%29%3Dx%5ET_NQ_fx_N%2C%20t%3DN%5C%5C%5C%5C%20Q_t%28x_t%2Cu_t%29%3Dx%5ET_tQx_t+u%5ET_tRu_t+V_%7Bt+1%7D%28x_%7Bt+1%7D%29$

这里同样假设存在一个矩阵 $eq?P_t$ （ $eq?P_t%3DP%5ET_t$ ）使得下式成立，

$eq?V_t%28x_t%29%3Dx%5ET_tP_tx_t$

那么基于离散状态方程 $eq?x_%7Bk+1%7D%3DAx_k+Bu_k$ ， $eq?Q_t$ 可以写为：

$eq?Q_t%28x_t%2Cu_t%29%3Dx%5ET_tQx_t+u%5ET_tRu_t+%28Ax_t+Bu_t%29%5ETP_%7Bt+1%7D%28Ax_t+Bu_t%29$

对于价值函数 $eq?Q_t$ 取极小值，即

$eq?%5Cfrac%7B%5Cpartial%20Q_t%7D%7B%5Cpartial%20u%7D%3D0$

这里插一个矩阵求导的知识（注意区分：分子布局还是分母布局）

$eq?y%3Dx%5ETAx%5C%5C%5C%5C%5Cfrac%7B%5Cpartial%20y%7D%7B%5Cpartial%20x%7D%3Dx%5ET%28A+A%5ET%29$

$eq?y%3DMx%5C%5C%5C%5CJ%3Dy%5ETSy%5C%5C%5C%5C%5Cfrac%7B%5Cpartial%20J%7D%7B%5Cpartial%20x%7D%3D%5Cfrac%7B%5Cpartial%20%28x%5ETM%5ETSMx%29%7D%7B%5Cpartial%20x%7D%5C%5C%5C%5C%3Dx%5ET%28M%5ETSM+M%5ETS%5ETM%29$

整理可得，

$eq?u%5ET_t%28R+R%5ET%29+%28Ax_t+Bu_t%29%5ET%28P_%7Bt+1%7D+P%5ET_%7Bt+1%7D%29B%3D0$

由于 $eq?R%2C%20P$ 都是对称矩阵，可得，

$eq?2u%5ET_tR+2%28Ax_t+Bu_t%29%5ETP_%7Bt+1%7DB%3D0$

$eq?u_t%3D-%28R%20+%20B%5ETP_%7Bt+1%7DB%29%5E%7B-1%7DB%5ETP_%7Bt+1%7DAx_t$

由 $eq?u%3D-Kx$ 可得，

$eq?K_t%3D%28R%20+%20B%5ETP_%7Bt+1%7DB%29%5E%7B-1%7DB%5ETP_%7Bt+1%7DA$

将 $eq?u_t$ 代入到 $eq?Q_t$ 中可得，

$eq?x%5ET_tP_tx_t%20%3D%20x%5ET_t%28Q+A%5ETP_%7Bt+1%7DA%20-%20A%5ETP_%7Bt+1%7DB%28R%20+%20B%5ETP_%7Bt+1%7DB%29%5E%7B-1%7DB%5ETP_%7Bt+1%7DA%29x_t$

最后得到的离散Riccati方程如下：

$eq?P_t%20%3D%20Q+A%5ETP_%7Bt+1%7DA%20-%20A%5ETP_%7Bt+1%7DB%28R%20+%20B%5ETP_%7Bt+1%7DB%29%5E%7B-1%7DB%5ETP_%7Bt+1%7DA$

在控制理论中，Riccati方程扮演着至关重要的角色，它通常用于描述线性时不变系统的最优控制问题。通过求解Riccati方程，可以找到使得系统状态达到最优的反馈控制律。对于离散时间系统和连续时间系统，Riccati方程的形式和求解方法会有所不同。

求解连续时间Riccati方程通常涉及数值方法，因为解析解可能不存在或难以找到。常用的数值方法包括迭代法和直接法。迭代法如牛顿法或不动点迭代法，通过迭代更新矩阵 P的值，直到满足收敛条件。直接法则试图通过矩阵分解或变换直接求解方程。

此部分的代码主要如下：

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/LU>
#include <iostream>using Eigen::Matrix;
using Eigen::Dynamic;typedef Matrix<double, Dynamic, Dynamic> Mtx;/** @brief Computes the LQR gain matrix (usually denoted K) for a discrete time* infinite horizon problem.** @param A State matrix of the underlying system* @param B Input matrix of the underlying system* @param Q Weight matrix penalizing the state* @param R Weight matrix penalizing the controls* @param N Weight matrix penalizing state / control pairs* @param K Pointer to the generated matrix (has to be a double/dynamic size* matrix!)* @param eps Delta between iterations that determines when convergence is* reached*/
bool SolveLQRMatrix(const Mtx &A, const Mtx &B, const Mtx &Q, const Mtx &R,const Mtx &N, Mtx *K, double eps = 1e-15) {// check if dimensions are compatibleif (A.rows() != A.cols() || B.rows() != A.rows() || Q.rows() != Q.cols() ||Q.rows() != A.rows() || R.rows() != R.cols() || R.rows() != B.cols() ||N.rows() != A.rows() || N.cols() != B.cols()) {std::cout << "One or more matrices have incompatible dimensions. Aborting."<< std::endl;return false;}// precompute as much as possibleMtx B_T = B.transpose();Mtx Acal = A - B * R.inverse() * N.transpose();Mtx Acal_T = Acal.transpose();Mtx Qcal = Q - N * R.inverse() * N.transpose();// initialize P with QMtx P = Q;// iterate until P convergesunsigned int numIterations = 0;Mtx Pold = P;while (true) {numIterations++;// compute new PP = Acal_T * P * Acal -Acal_T * P * B * (R + B_T * P * B).inverse() * B_T * P * Acal + Qcal;// update deltaMtx delta = P - Pold;if (fabs(delta.maxCoeff()) < eps) {std::cout << "Number of iterations until convergence: " << numIterations<< std::endl;break;}Pold = P;}// compute K from P*K = (R + B_T * P * B).inverse() * (B_T * P * A + N.transpose());return true;
}

3 车辆LQR控制

本小节以汽车运动学模型为例，车辆的运动模型如下图所示，本小节理论部分主要参考龚建伟老师著作《无人驾驶车辆模型预测控制》，基于汽车动力学模型的推导可参考Rajamani的著作《Vehicle Dynamics And Control》。

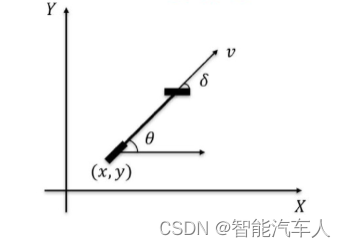
3.1 运动学模型

可得车辆的运动学模型为：

$L%20%7D%20%5Cend%7Bbmatrix%7D*v_r$ $eq?$

可将整个系统看作一个输入为 $eq?u%28v%2C%5Cdelta%20%29$ 和 $eq?%5Cchi%20%28x%2Cy%2C%5Cvarphi%20%29$ 的控制系统。其一般形式为：

$eq?%5Cdot%7B%5Cchi%7D%3Df%28%5Cchi%2Cu%29$

在自动驾驶轨迹跟踪中，通常以跟踪偏差作为输入，因此可得，

$eq?%5Cdot%7B%5Cchi%7D%3Df%28%5Cchi_r%2Cu_r%29+%5Cfrac%7B%5Cpartial%28%5Cchi%2Cu%29%20%7D%7B%5Cpartial%20%5Cchi%7D%7C_%7B%5Cchi%3D%5Cchi_r%2Cu%3Du_r%7D%28%5Cchi-%5Cchi_r%29+%5Cfrac%7B%5Cpartial%28%5Cchi%2Cu%29%20%7D%7B%5Cpartial%20u%7D%7C_%7B%5Cchi%3D%5Cchi_r%2Cu%3Du_r%7D%28u-u_r%29$

$%28lcos%5E2%5Cdelta_r%29%20%5Cend%7Bbmatrix%7D%5Cbegin%7Bbmatrix%7D%20v-v_r%5C%5C%20%5Cdelta-%5Cdelta_r%20%5Cend%7Bbmatrix%7D$

为了能够将该模型应用于控制器的设计，最终进行离散化处理，最终可以写成如下形式： $eq?%5Ctilde%7B%5Cchi%7D%28k+1%29%3D%20A%5Ctilde%7B%5Cchi%7D%7Bk%7D+B%5Ctilde%7Bu%7D%28k%29$

$%28lcos%5E2%5Cdelta_r%29%20%5Cend%7Bbmatrix%7D$

建立运动学模型的代码如下（只保留重要部分）：

void Model::GetModel(float curvature, Eigen::Matrix<double, 3, 1> state_actual){//target delta is variable because of curve path.float target_delta = atan(wheel_base*curvature); //dphi/dt = V*tan(delta)/L;  w = V*tan(delta)/L/*****************************************************/// AMatrix_->A(0, 0) = 1;Matri>A(1, 0) = 0;Matrix_->A(1, 1) = 1;Matrix_->Ax_->A(0, 1) = 0;Matrix_->A(0, 2) = -target_velocity*sin(state_actual(2,0))*dt_;Matrix_-(1, 2) = target_velocity*cos(state_actual(2,0))*dt_;Matrix_->A(2, 0) = 0;Matrix_->A(2, 1) = 0;Matrix_->A(2, 2) = 1;/*****************************************************/// BMatrix_->B(0, 0) = cos(state_actual(2,0))*dt_;Matrix_->B(0, 1) = 0;Matrix_->B(1, 0) = sin(state_actual(2,0))*dt_;Matrix_->B(1, 1) = 0;Matrix_->B(2, 0) = tan(target_delta)*dt_/wheel_base;Matrix_->B(2, 1) = target_velocity*dt_/(wheel_base*(cos(target_delta)*cos(target_delta)));
}

3.2 求解

再结合上面一节LQR求解代码如下（非完整）：

void LQRControl::LQRController(){//near pointint index = FindMatchedPoint(actual_pos.x, actual_pos.y);x_ref_(0, 0) = planning_path[index].position.x;x_ref_(1, 0) = planning_path[index].position.y;x_ref_(2, 0) = planning_path[index].position.yaw;x_act_(0, 0) = actual_pos.x;x_act_(1, 0) = actual_pos.y;x_act_(2, 0) = actual_pos.yaw;/***********compute curvature of target point********************************/curvature = ComputeCurvature(index);// get model matrix A and Bmodel_.GetModel(curvature, x_act_);matrix_c.A = model_.Matrix_->A;matrix_c.B = model_.Matrix_->B;// Q(3x3): positive semi-definite matrix, penalizing the statematrix_c.Q(0, 0) = 1;matrix_c.Q(0, 0) = 10;matrix_c.Q(0, 0) = 1;// R(2x2): positive definite matrix,  penalizing the controlsmatrix_c.R(0, 0) = 100;matrix_c.R(1, 1) = 100;// N(3x2):  penalizing the state/control pairsmatrix_c.N = Eigen::Matrix<double, 3, 2>::Zero();/****************************************************************************/// Solve the Riccati Equationif (!SolveLQRMatrix(matrix_c.A, matrix_c.B, matrix_c.Q, matrix_c.R, matrix_c.N, &matrix_k)){std::cout << "Compute matrix K failed!" << std::endl;}else{std::cout << matrix_k << std::endl;}
}