【知识学习/复习】损失函数篇，包含理解应用与分类：回归、分类、排序、生成等任务

损失函数总结

一、损失函数理解
二、不同任务的损失函数的应用
- - 1.图像分类
  - 2.目标检测
  - 3.语义分割
  - 4.自然语言处理（NLP）
  - 5.图神经网络（GNN）
  - 6.生成式网络
三、损失函数
- 1. 回归任务损失函数
- - 常见损失函数
  - IoU系列损失函数
  - - 1. IoU损失函数（基础版）
    - 2. GIoU损失函数（Generalized IoU）
    - 3. DIoU损失函数（Distance IoU）
    - 4. CIoU损失函数（Complete IoU）
    - 其他iou：
    - 总结：
- 2. 分类任务损失函数
- 3. 排序任务损失函数
- 4. 生成任务损失函数

一、损失函数理解

损失函数（Loss Function），在机器学习和统计学中，是一个衡量模型预测值与实际值之间差异的函数。

损失函数的目的是量化模型的预测误差，以便在训练过程中通过优化算法（如梯度下降）来最小化这个误差，从而提高模型的预测准确性。
损失函数的选择取决于问题的性质和模型的类型。比如：
1.均方误差（Mean Squared Error, MSE）：常用于回归问题，计算预测值与实际值差的平方的平均值。
2.交叉熵损失（Cross-Entropy Loss）：常用于分类问题，衡量模型预测的概率分布与真实分布之间的差异。
3.对数损失（Log Loss）：是交叉熵损失的一种特殊情况，常用于二分类问题。
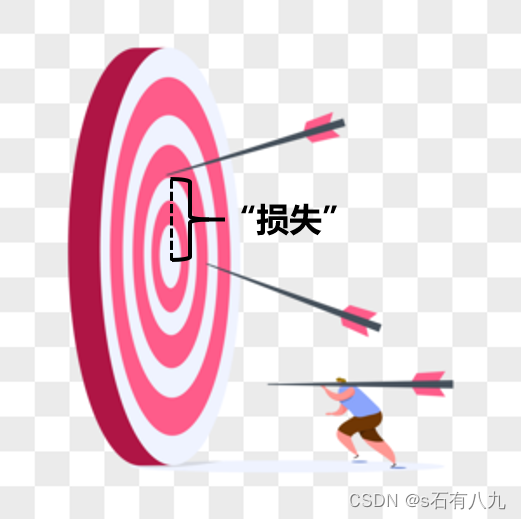
通俗理解：想象一下，你是一名射箭运动员，你的目标是射中靶心。每次射箭后，箭落在靶子上的位置与靶心之间的距离，可以看作是你的“损失”。你的任务是通过不断练习，调整你的射箭技巧，使得这个距离尽可能小。
▲在这个比喻中：
靶心：代表实际值，也就是你想要达到的目标。
你的箭：代表模型的预测值。
箭与靶心的距离：代表损失函数的输出，即预测值与实际值之间的差异。
损失函数的作用就是计算这个“距离”，告诉你离目标还有多远。在机器学习中，我们通过不断调整模型（就像运动员调整射箭技巧），来减小这个“距离”，也就是最小化损失函数的值，从而使模型的预测更加准确。
选择不同的损失函数，就像是选择不同的衡量距离的方法。

二、不同任务的损失函数的应用

在机器学习和深度学习的多个领域中，损失函数的选择对于模型性能至关重要。以下是不同任务中常用的损失函数：

1.图像分类

交叉熵损失（Cross-Entropy Loss）：用于多分类问题，衡量模型输出的概率分布与真实标签的概率分布之间的差异。
sigmoid 交叉熵损失：适用于二分类任务和多标签分类问题，度量每个类独立且不互斥的概率误差。

2.目标检测

IoU损失（Intersection over Union Loss）：基于预测边界框和真实边界框之间的IoU，衡量两个矩形框的重叠程度。
GIoU损失（Generalized IoU Loss）：在IoU损失的基础上增加了惩罚项，解决非重叠情况下的梯度消失问题。
DIoU损失（Distance IoU Loss）：考虑了预测框与真实框中心点的归一化距离，尺度不变。
CIoU损失（Complete IoU Loss）：在DIoU损失的基础上增加了对纵横比的考虑，提供了更全面的几何因子。

3.语义分割

交叉熵损失：用于像素级别的分类，计算每个像素点的分类概率与真实标签之间的差异。
Dice系数：衡量两个集合的相似度，通常用于计算分割图像的相似度。
Tversky损失：是Dice系数的扩展，通过调整参数控制假阳性和假阴性的相对重要性。

4.自然语言处理（NLP）

交叉熵损失：用于文本分类、机器翻译等任务，衡量预测概率与真实标签之间的差异。
语言模型（Language Modeling）：语言模型的目标是预测给定上下文的下一个单词或字符。常见的损失函数包括交叉熵损失函数（Cross-Entropy Loss）和负对数似然损失函数（Negative Log-Likelihood Loss）。

文本分类（Text Classification）：文本分类任务涉及将文本分为不同的预定义类别。常见的损失函数包括交叉熵损失函数和多项式逻辑回归损失函数（Multinomial Logistic Regression Loss）。
序列标注（Sequence Labeling）：序列标注任务涉及对输入序列中的每个标记进行分类。例如，命名实体识别（Named Entity Recognition）和词性标注（Part-of-Speech Tagging）等任务。常见的损失函数包括交叉熵损失函数和条件随机场损失函数（Conditional Random Field Loss）。
机器翻译（Machine Translation）：机器翻译任务涉及将源语言文本翻译成目标语言文本。常见的损失函数包括交叉熵损失函数和最大似然损失函数（Maximum Likelihood Loss）。
序列生成（Sequence Generation）：序列生成任务涉及生成符合某种规则的序列，例如文本摘要（Text Summarization）和机器对话（Chatbot）等任务。常见的损失函数包括交叉熵损失函数、自定义的目标函数（例如，基于BLEU分数的损失函数）以及强化学习中的策略梯度损失函数（Policy Gradient Loss）。

5.图神经网络（GNN）

基于重构损失的GNN：通过最小化节点重构的误差来进行图结构数据的表示学习。
基于对比损失的GNN：使用对比学习的方法来学习图结构数据的表示。

6.生成式网络

均方误差损失（Mean Squared Error, MSE）：常用于生成对抗网络（GAN）中，衡量生成图像与真实图像之间的差异。

在实际应用中，损失函数的选择和设计对于模型能否有效学习以及其最终性能具有决定性作用。此外，损失函数的组合使用或者变种设计也常常根据具体任务的需求来进行调整。

三、损失函数

按任务类型分类，损失函数可以分为以下几类，并且我将为每个类别提供具体的例子：

1. 回归任务损失函数

回归任务的目标是预测一个连续值，常用损失函数包括：
任务: 预测一个连续值，如房价、温度等。

均方误差（Mean Squared Error, MSE）:
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$ MSE是真实值与预测值的差值的平方然后求和平均。其中， $y_i$ 是真实值， $\hat{y}_i$ 是预测值。

常见损失函数

均方根误差（Root Mean Squared Error, RMSE）:
$\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}$ 均方根误差是预测值与真实值偏差的平方与观测次数n比值的平方根。衡量的是预测值与真实值之间的偏差，并且对数据中的异常值较为敏感。
平均绝对误差（Mean Absolute Error, MAE）:
$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|$
通俗解释：
想象你是一名学生，每次考试后，老师会检查你答对的题目数量。在MAE的情况下，老师不会关心你答对的题目比别人多多少，只会简单地数一数你答错了多少题，然后计算全班平均每个学生答错的题目数量。在机器学习中，这就像是计算模型预测值与实际值之间差异的总和，然后取平均值。
Huber损失:
$L_{\delta}(a) = \begin{cases} \frac{1}{2}a^2 & \text{for } |a| \le \delta, \\ \delta |a| - \frac{1}{2}\delta^2 & \text{otherwise}, \end{cases}$
其中 $y_i - \hat{y}_i$ ， $\delta$ 是一个阈值。
Huber损失可以看作是MAE和MSE的结合。 它对小的误差（比如小于某个阈值δ）使用平方惩罚，而对大的误差使用线性惩罚。这就像是老师对学生的答错题目数量有一个容忍度，当学生答错的题目少于这个数量时，老师会严苛地惩罚；但一旦超过这个数量，老师会认为学生可能需要额外的帮助而不是惩罚，因此惩罚会变得轻一些。

IoU（交并比，Intersection over Union）及其衍生的损失函数是目标检测领域中用于评估预测边界框与真实边界框之间相似度的关键工具。以下是IoU及其发展至今的多种变体损失函数的介绍，以及它们通俗易懂的解释：

IoU系列损失函数

1. IoU损失函数（基础版）

通俗解释：
IoU损失函数是最直观的衡量预测边界框与真实边界框相似度的方法。如果预测框和真实框完全不重叠，IoU为0，损失为1；如果完全重合，IoU为1，损失为0。这就像是用一个橡皮圈去套一个固定在地面上的小物体，橡皮圈和物体重叠的区域除以橡皮圈整个区域的大小，就是IoU。
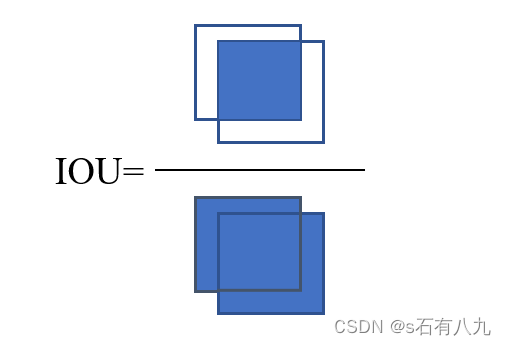
在这里插入图片描述

数学公式：
$\text{IoU} = \frac{\text{A∩B}}{\text{A∪B}}$
缺点：

非重叠时的梯度问题：当预测边界框和真实边界框没有重叠时，IoU值为0，此时IoU损失函数的梯度也为0，导致无法通过梯度下降法来优化模型。
尺度敏感性：IoU对边界框的尺度变化比较敏感，这可能导致在不同尺度的目标上性能不稳定。
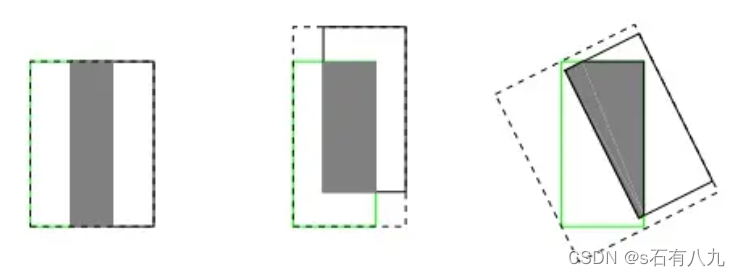
无法精确反映重合度：IoU无法精确反映两个边界框的重合程度，特别是当两个框部分重叠或者角度差异较大时。下面三个iou相同，但可以看出重合度是不同的。

2. GIoU损失函数（Generalized IoU）

通俗解释：
GIoU损失函数在IoU的基础上增加了一个惩罚项，这个惩罚项是两个边界框的最小闭合框与它们实际面积的比值。当两个框不重叠时，IoU为0，但GIoU损失仍然可以提供梯度，帮助模型学习。
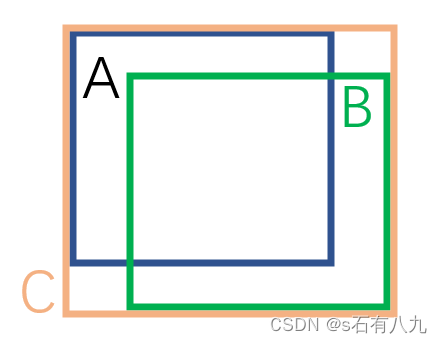
在这里插入图片描述

数学公式：
$\text{GIoU} = IoU-\frac{\text{C}-\text{(A∩B)}}{\text{C}}$ 其中C是两个框的最小外接矩形的面积
解决的问题：

梯度消失问题： 当预测边界框和真实边界框没有重叠时，IoU为0，其梯度也为0，导致无法提供有意义的反馈给模型。GIoU通过引入最小闭合框（smallest enclosing box）的概念，即使在非重叠情况下也能提供梯度，从而解决了这个问题。
尺度敏感性： GIoU考虑了预测框和真实框的面积，使得损失函数对尺度更敏感，有助于模型学习到更准确的边界框尺寸。

3. DIoU损失函数（Distance IoU）

通俗解释：
DIoU损失函数在GIoU的基础上，进一步考虑了预测框和真实框中心点之间的距离。这就像是不仅考虑橡皮圈和物体的重叠程度，还要考虑橡皮圈中心与物体中心的距离。

数学公式：
$L_{\text{DIoU}} = 1 - \text{IoU} - \text{Center Distance Term}$
$\text{Center Distance Term} = \frac{\rho^2}{c^2}$

其中， $\rho$ 是预测框与真实框中心点的距离， $c$ 是最小闭合框的对角线长度。

4. CIoU损失函数（Complete IoU）

通俗解释：
CIoU损失函数是DIoU的扩展，它不仅考虑重叠区域和中心点距离，还考虑了两个框的宽高比。这就像是在橡皮圈游戏中增加了一个规则，如果橡皮圈和物体的形状接近，也会得到额外的分数。

数学公式：
$L_{\text{CIoU}} = 1 - \text{IoU} - \text{Center Distance Term} - \text{Aspect Ratio Term}$
$\text{Aspect Ratio Term} = \beta(v) \left( \frac{4}{\pi^2} \arctan \frac{w_p}{h_p} - \frac{1}{4} \right)$

其中， $\beta(v)$ 是一个根据重叠区域面积调整权重的函数， $v$ 是预测框与真实框重叠区域的面积， $w_p$ 和 $h_p$ 分别是预测框和真实框的宽度和高度。

其他iou：

SIoU (Smooth IoU): SIoU损失函数通过融入角度考虑和规模敏感性，引入了一种更为复杂的边界框回归方法。它包含角度损失、距离损失、形状损失等组成部分，旨在实现更好的训练速度和预测准确性。
EIoU (Enhanced IoU): EIoU损失函数的核心在于提高边界框回归的准确性和效率。它通过增加中心点距离损失、考虑尺寸差异以及结合最小封闭框尺寸来优化目标检测。
WIoU (Wise IoU): WIoU损失函数引入了动态聚焦机制，旨在改善边界框回归损失，适用于需要动态调整损失焦点的情况，如不均匀分布的目标或不同尺度的目标检测。
XIoU、NWD、RepulsionLoss: 这些损失函数是YOLOv8提出的70多种IoU损失函数的改进之一，用于进一步优化目标检测性能。

总结：

从IoU到CIoU的发展，反映了目标检测领域对于边界框预测精度要求的提高。每种损失函数都试图以不同的方式解决边界框预测中的特定问题，如非重叠情况下的梯度消失、尺度不变性、以及形状相似性等。通过这些损失函数的应用，目标检测模型能够更准确地定位图像中的对象。

2. 分类任务损失函数

分类任务的目标是预测离散类别的标签，常用损失函数包括：
任务: 预测一个离散类别，如垃圾邮件检测、手写数字识别等。

二元交叉熵损失（Binary Cross-Entropy Loss）: 用于二分类问题。
$-\left( y_i \cdot \log(\hat{y}_i) + (1 - y_i) \cdot \log(1 - \hat{y}_i) \right)$ 假设我们有一个二分类问题，比如判断邮件是否为垃圾邮件。这个损失函数衡量的是模型认为邮件是垃圾邮件的概率与实际标签（是或否）之间的差异。
多类交叉熵损失（Categorical Cross-Entropy Loss）: 用于多分类问题。
$-\sum_{c=1}^{M} y_{ic} \cdot \log(\hat{y}_{ic})$ 对于有多于两个类别的问题，比如手写数字识别（0到9的数字）。这个损失函数衡量的是模型对每个类别预测概率的分布与真实标签的分布之间的差异。其中， $M$ 是类别的数量， $y_{ic}$ 是一个指示器，当类别 $c$ 是正确的类别时为1，否则为0。
Hinge损失（Hinge Loss）: 支持向量机（SVM）中使用。
$\max(0, 1 - (y_i \cdot \hat{y}_i))$
例子： 假设你正在尝试区分猫和狗的图片。如果一张图片是猫，那么它的正确标签是-1。如果模型预测图片是猫（即输出了一个负值），并且很准确，那么 $y_i \cdot \hat{y}_i$ 会是一个较大的负数，乘积为正值，Hinge损失就会是0，因为模型已经很好地分类了这个样本。反之，如果模型预测是一个正值（认为图片是狗），那么损失就会是一个正数，意味着模型犯了一个错误，需要调整。
Focal损失（Focal Loss）:
Focal损失是为了解决类别不平衡问题而提出的。在一些情况下，某些类别的样本数量可能远多于其他类别，导致模型对多数类过拟合，而对少数类则难以学习。Focal损失通过减少对“简单”样本（即模型已经很好分类的样本）的关注，而增加对“困难”样本（模型分类不够准确的样本）的关注来解决这个问题。这就像是老师在课堂上决定花更多的时间帮助那些学习有困难的学生，而不是已经表现很好的学生。
$-\alpha_t (1 - \hat{y}_i)^{\gamma} \cdot \log(\hat{y}_i)$
其中， $\alpha_t$ 是平衡因子， $\gamma$ 是调节因子。
例子： 继续上面猫狗图片分类的例子，假设“猫”类别的图片非常多，而“狗”类别的图片非常少。如果模型大多数时间都在学习区分不同种类的“猫”，而对“狗”的图片关注不足。使用Focal损失后，模型会对那些分类错误的“狗”图片给予更多的权重，从而鼓励模型更关注少数类，改善分类性能。

3. 排序任务损失函数

排序任务通常涉及到对一组项进行排序，常用损失函数包括：
任务: 预测项目之间的相对顺序，如搜索引擎结果排序。

Pairwise排序损失: 如三元组损失（Triplet Loss）。
用于训练一个系统，比如面部识别，要求系统能够识别出人脸之间的相似性或差异性。三元组损失会取一个锚点样本，一个相似样本和一个不同样本，然后确保锚点与相似样本之间的距离小于锚点与不同样本之间的距离。
$\sum_{i=1}^{n} \max(0, d(a_i, p_i) - d(a_i, n_i) + margin)$
其中 $a_i$ 是锚点， $p_i$ 是正样本， $n_i$ 是负样本， $d$ 是样本之间的距离， $ma r g in$ 是边界。
Listwise排序损失: 如直接优化排序任务的NDCG（Normalized Discounted Cumulative Gain）。

4. 生成任务损失函数

生成任务如生成对抗网络（GANs）中使用特殊的损失函数：
任务: 创建新的数据实例，如生成图片、音乐等。

最小二乘GAN（Least Squares GAN）:
$L_D = \frac{1}{n} \sum_{i=1}^{n} (D(x_i) - r)^2$
$L_G = \frac{1}{n} \sum_{i=1}^{n} (D(G(z_i)) - (1 - r))^2$
其中 $D$ 是判别器， $G$ 是生成器， $r$ 是介于0和1之间的常数。
Wasserstein损失: 提高GAN训练的稳定性。
用于生成对抗网络（GANs），比如生成看起来像梵高画风的图片。这个损失函数能够更稳定地训练GAN，通过最大化真实图片与生成图片之间的Wasserstein距离。
$L_D = \sum_{i=1}^{n} D(x_i) - \mathbb{E}_{q(z)} [D(G(z))]$
$L_G = -\mathbb{E}_{q(z)} [D(G(z))]$
其中 $q (z)$ 是先验噪声分布。

这些损失函数的选择和设计对于模型能否有效学习和其最终性能至关重要。在设计损失函数时，研究人员会考虑任务特性、模型架构以及训练目标。