目录
一.B树介绍
(一).B树存在意义
(二).B树的规则
二.B树实现原理及代码
(一).实现原理
(二).代码
三.B+树
(一).概念
(二).应用
①MyISAM
②InnoDB
四.B*树

一.B树介绍
(一).B树存在意义
B树主要用于磁盘文件的检索操作。众所周知,平衡二叉树(AVL树、红黑树)搜索的时间复杂度是O(log^n)。虽然很快,但如果数据在磁盘中且有上亿量级的数据,即便只有30次左右的IO操作,速度也是非常慢的。因为磁盘IO速度极慢,主要是寻道操作影响,平均8ms左右。
因此,磁盘数据的检索不适合使用平衡二叉树,B树正式上线。
B树可以看成是压缩版的平衡二叉树,每一个节点上都有保存有多个值,且有多个叶子节点。
一般而言,B树的检索次数在个位量级,这取决于每个节点上能保存多少个值。
上亿量级的数据,红黑树可能需要30次左右,但B树只需要3-4次即可。
(二).B树的规则
1. 根节点至少有两个孩子,规定每个节点最多存m - 1个元素
2. 每个分支有k - 1个元素和k个孩子节点,其中 ceil(m/2) ≤ k ≤ m,ceil是向上取整函数。
即孩子节点个数 = 元素个数 + 1(必须是分支节点)
3. 每个叶子节点都包含k-1个元素,其中 ceil(m/2) ≤ k ≤ m
4. 所有的叶子节点都在同一层
5. 每个节点中的元素从小到大排列
二.B树实现原理及代码
(一).实现原理
以插入3、6、4、2、7、1、5为例,假定m为3,即每个节点最多存2个元素
首先,B树的节点图示如下:
这里多开辟一个空间是为了当元素数量满3时便于之后分裂。
 依次插入,注意插入后元素要按从小到大排列(直接插入排序):
依次插入,注意插入后元素要按从小到大排列(直接插入排序):

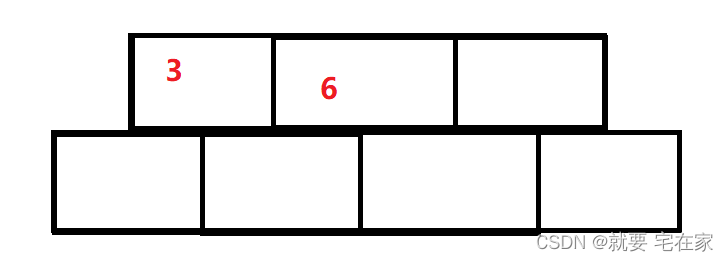

此时,元素数量已经满3,要进行分裂操作。
分裂:节点对半分裂,将4提出作为父节点(根节点),3和6叶子节点分别作为4的左右孩子节点

之后2与4比较并插入,插入位置均是叶子节点(所有插入的元素都是这样)。

2小于4,因此插入左叶子节点,之后与3比较,小于3,插入左边。

7大于4因此插入右叶子节点,大于6,插入6右边

插入1后,此时右叶子节点满3了,要进行分裂:
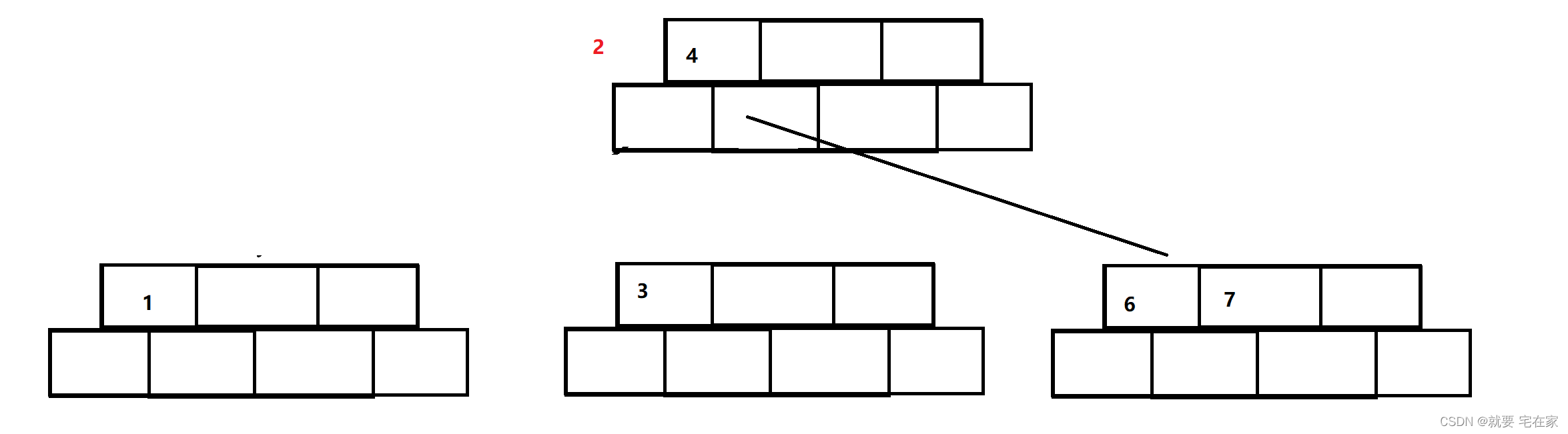
分裂方式一样,将2提至父节点,1和3对半分。

2比4小,将4后移,同时4的右子树后移,1作为2的左子树,3作为2的右子树。
 5插入后,4的右子树满3,进行分裂:
5插入后,4的右子树满3,进行分裂:
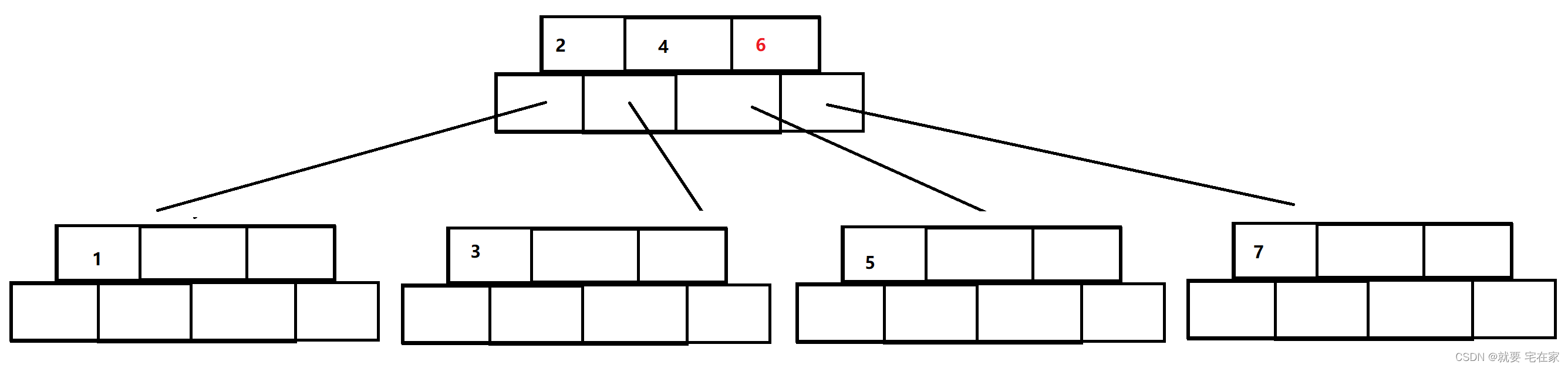 此时根节点满3,也要分裂:
此时根节点满3,也要分裂:

将4提出作为根节点,2和6对半分,各自的叶子节点也对半分。
以上步骤包括所有B树插入的可能情况。
(二).代码
// - - - : _key
//- - - - : _child
template<class T, size_t M>
struct BTreeNode {size_t _n;//已有值数量T _key[M + 1];//存放值,多一个位置,便于满时添加BTreeNode* _child[M + 1];//存放子节点们地址BTreeNode* _parent;//父节点BTreeNode()//初始化 + 默认构造:_n(0),_parent(nullptr){for (size_t i = 0; i <= M; i++) {_key[i] = T();_child[i] = nullptr;}}
};template<class T, size_t M>
class BTree {typedef BTreeNode<T, M> Node;void _insertKey(Node* cur, const T& key, Node* child)//child:右孩子{int i = cur->_n - 1;for (; i >= 0; i--)//这里不需要再判断key是否已有,insert中已经判断{if (key < cur->_key[i])//数据后移{cur->_key[i + 1] = cur->_key[i];cur->_child[i + 2] = cur->_child[i + 1];}else//key小于当前数据{break;}}// - - - _key// - - - - _child// ^ ^// i childcur->_key[i + 1] = key;cur->_child[i + 2] = child;if (child){child->_parent = cur;}cur->_n++;}
public:pair<Node*, int> find(const T& key)//寻找节点{Node* cur = _root;Node* parent = nullptr;while (cur){int i = 0;while (i < cur->_n){if (key > cur->_key[i]){i++;}else if (key < cur->_key[i]){break;}else{return make_pair(cur, i);}}parent = cur;cur = cur->_child[i];}return make_pair(parent, -1);//没有找到}bool insert(const T& key)//插入值{if (_root == nullptr)//插入的是第一个节点{_root = new Node;_root->_key[0] = key;_root->_n++;return true;}//插入的不是第一个节点pair<Node*, int> ret = find(key);//找节点if (ret.second >= 0) return false;//节点已经存在//节点不存在,进行插入操作Node* cur = ret.first;Node* brother = nullptr;T midValue = key;//因为key是const,不能直接使用while (1){_insertKey(cur, midValue, brother);//先插入//判断cur是否已经满了if (cur->_n == M){//满了,分裂brother = new Node;T keyValue = cur->_key[M / 2];cur->_key[M / 2] = T();int i = M / 2 + 1, j = 0;for (; i < M; i++)//分裂{brother->_key[j] = cur->_key[i];brother->_child[j] = cur->_child[i];cur->_key[i] = T();cur->_child[i] = nullptr;if (brother->_child[j]){brother->_child[j]->_parent = brother;}j++;}brother->_n = j;cur->_n = M - brother->_n - 1;//-1是因为还要把向上提到父节点的减去brother->_child[j] = cur->_child[M];//最后一个子节点也需要添加cur->_child[M] = nullptr;if (brother->_child[j]){brother->_child[j]->_parent = brother;}//判断cur是否是根节点,是就需要手动创建节点并链接叶子,因为_insertKey只能同层插入,不能更新_rootif (cur->_parent == nullptr){_root = new Node;_root->_key[0] = keyValue;_root->_child[0] = cur;_root->_child[1] = brother;cur->_parent = _root;brother->_parent = _root;_root->_n = 1;break;}else{midValue = keyValue;cur = cur->_parent;}}else{break;}}return true;}void levelOrder()//层序遍历{queue<Node*> qu;qu.push(_root);while (!qu.empty()){int n = qu.size();while (n--){Node* node = qu.front();qu.pop();int i = 0;for (; i < node->_n; i++){cout << node->_key[i] << " ";if (node->_child[i]){qu.push(node->_child[i]);}}if (node->_child[i]){qu.push(node->_child[i]);}cout << "| ";}cout << endl;}}private:Node* _root = nullptr;
};三.B+树
(一).概念
B+树是对B树的改进,具体改进如下:
1.分支节点的子树指针与元素个数相同
2. 所有叶子节点增加一个链接指针链接在一起,便于遍历元素
3. 所有元素都在叶子节点出现,且链表中的节点都是有序的
4.分支节点相当于是叶子节点的索引,叶子节点才是存储数据的数据层,叶子层的元素才记录与数据的映射。
5.分支、叶子节点首元素来自父节点,且首元素是本节点最小元素(便于查找时确定位置)
图例如下:
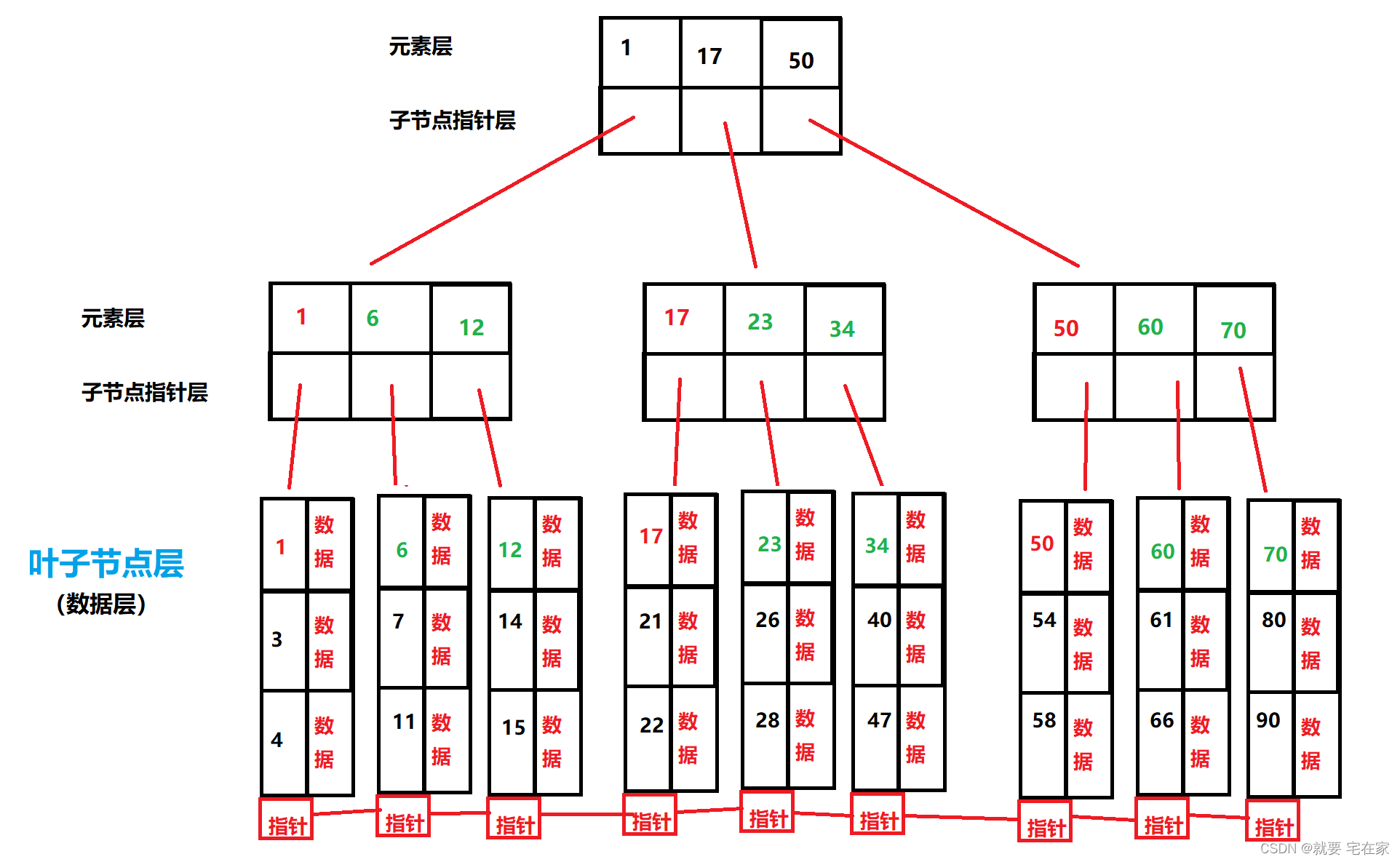
分支节点可以看成是叶子节点的索引,链接指针存在的意义就是便于遍历所有数据,通过叶子节点的指针可以访问兄弟叶子节点,进而遍历数据。
插入数据时,如果叶子节点元素满了就创建一个新节点,并将数据的后一半给新节点,在父节点中记录新节点第一个数据并建立指针联系。
(二).应用
B+树典型应用就是MySQL的索引。
①MyISAM
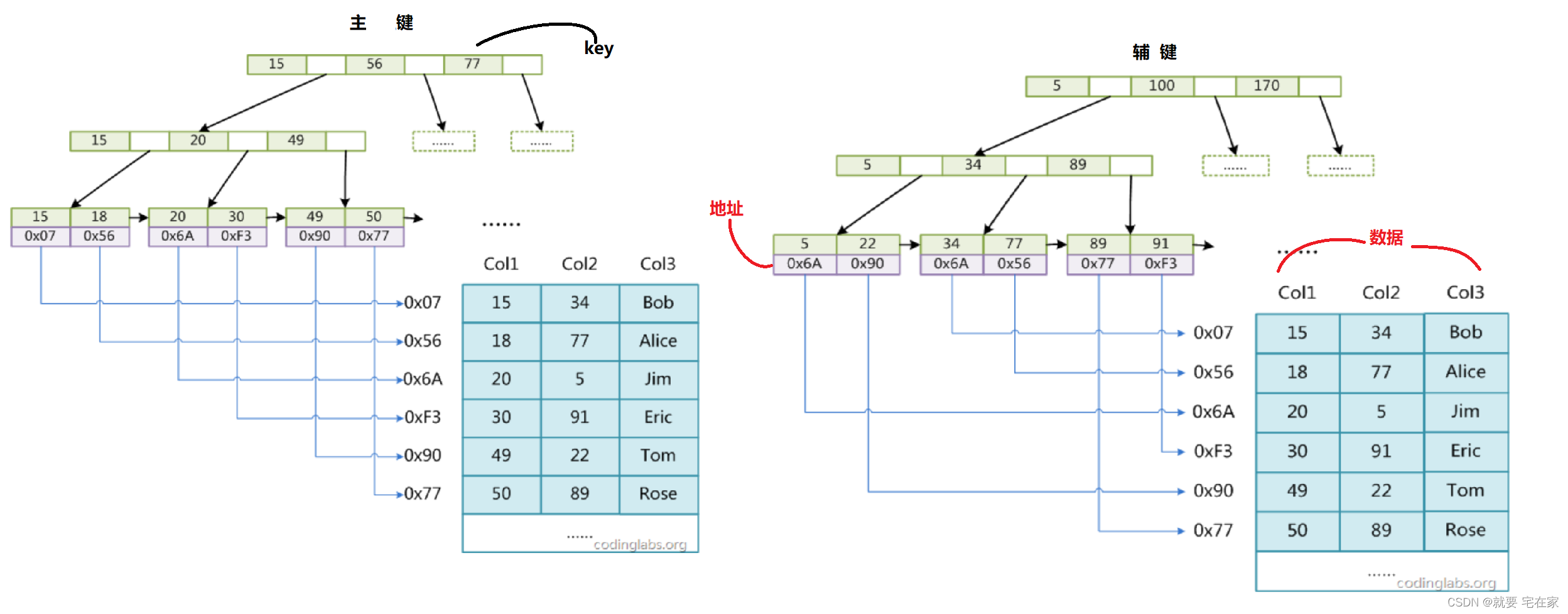
MySQL中的MyISAM引擎就是使用B+树,主键和辅键索引结构相同,只不过主键不能重复,索引数据时,通过B+树的搜索方式(与B树基本相同,不同是可以通过链接指针直接访问下一个叶子节点)找到key值,通过key值找到数据地址,再通过地址访问数据,即非聚集索引。
图例如下:
图示来源(有修改):CodingLabs - MySQL索引背后的数据结构及算法原理
②InnoDB
InnoDB是MySQL的默认存储引擎,与MyISAM不同的是:
1.数据文件本身就是按B+树组织的结构,即主键索引。而MyISAM的主键索引与数据文件分离,记录的是数据文件地址。
2.辅键索引映射主键的值。而MyISAM的辅键索引映射的是数据文件地址
使用主键索引时非常高效,可以直接得到完整的数据,但是使用辅键索引时需要先索引出主键值,再根据主键值索引出数据,即聚集索引。
图例如下:
图示来源(有修改):CodingLabs - MySQL索引背后的数据结构及算法原理

四.B*树
B*树是对B+树的进一步改良,它优化了B+树的空间利用率。
结构上是在B+树基础上,分支节点中再增加指向兄弟分支节点的指针。
图例如下:
插入数据时,如果叶子节点满了,就将一部分数据给兄弟节点。如果兄弟节点满了就进行分裂,在自己与兄弟节点中间创建新节点,将自己与兄弟节点各1/3数据给新节点并与父节点建立联系。
退一步海阔天空,这是一种应有的心境——未名
如有错误,敬请斧正