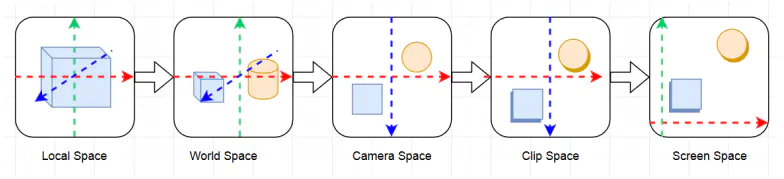
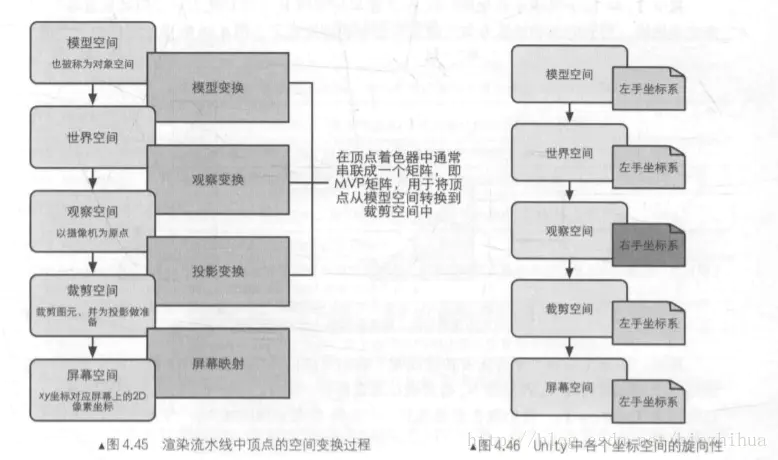
模型空间->世界空间->视口空间：

比较容易理解，就是用矩阵进行缩放旋转和平移

 

视口空间（右手坐标系）-> 齐次裁剪空间（左手坐标系）:

下文中的n代表near,f代表far,fov代表FOV

设视口空间坐标点为Vp = {Vx, Vy, Vz}，摄像机前方的Vz为负数，裁剪空间坐标点为Cp = {Cx, Cy, Cz, Cw}

则裁剪空间的未映射坐标是：Cp = {Cx, Cy, Cz, Cw} = {Vx * n, Vy * n,  a*Vz + b, -Vz}，

此时对Cp进行透视除法，得到的x，y范围是[left, right]和[bottom, top]

若对x，y从[left, right]和[bottom, top]映射到[-1, 1],则可以得到正确的裁剪坐标如下：

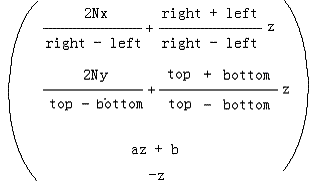
对此时的裁剪坐标进行透视除法，得到的x，y的范围是[-1, 1]

推导请查看：https://blog.csdn.net/zengjunjie59/article/details/109572857

变换到齐次裁剪空间后不同类型API得到的取值范围不同：

类 OpenGL 齐次裁剪空间得到的数值范围

Cx∈[-Cw, Cw],  Cy∈[-Cw, Cw],  Cz∈[-Cw, Cw]，从视锥体角度看Cz∈[-near, far],  Cw = -Vz，明显，随着|Vz|的增大，|Cx|和|Cy|会随着增大（即视锥体的形状）

类 DX 齐次裁剪空间得到的数值范围

Cx∈[-Cw, Cw],  Cy∈[-Cw, Cw],  Cz∈[0, Cw], 从视锥体角度看Cz ∈ [ 0, far], Cw = -Vz某些平台下，会定义UNITY_REVERSED_Z，此时则Cz∈[Cw, 0]，越靠近屏幕，Cz越接近Cw，这是为了提高近距离的深度精度，, 从视锥体角度看, Cz ∈ [near, 0]（越靠近近裁切面，Cz越接近near）

详细解析：https://blog.csdn.net/acmhonor/article/details/106167261

官方文档：https://docs.unity3d.com/cn/current/Manual/SL-PlatformDifferences.html

需要注意的是:

在顶点着色器中使用UnityObjectToClipPos函数把模型空间顶点变换到裁剪空间的时候，在顶点着色器中该坐标是裁剪空间下的坐标，但是如果通过SV_POSITION语义传到片元着色器之后，该坐标会被自动变换到了屏幕坐标下，此时的x和y已经是屏幕坐标了。

 

 

Cp是齐次坐标，并且是线性相关的，即均匀更变X的时候Z也是均匀更变的（导数为常数的一次函数），可以进行线性插值，：

设Vy不变，       Vz与Vx是线性相关的（图像是一条直线）。

Cx = Vx * n，    Cx与Vx是线性相关。

Cz = a*Vz + b,  Cz与Vz是线性相关。

由于线性相关的传递性，所以Cx与Cz线性相关，y同理，所以Cp = {Cx, Cy, Cz, Cw} 裁剪坐标间可进行线性插值

例子（忽略y值，y与x同理）：

需得到Cz和Cx的关系，即：Cz = f(Cx)

由于Vz和Vx是线性关系，

所以有（1）Vz = cVx + d 

（2）Cx = nVx  

（3）Cz = aVz + b   

三式联立：

Cz = f(Cx) = aVz+ b = a(cVx + d) + b = acVx + ad + b = ac(Cx/n) + ad + b = ac/nCx + ad + b

即：Cz = ac/nCx + ad + b， 所以Cz和Cx是线性关系

 

齐次裁剪空间 -> 屏幕空间:

裁剪后需要进行真正的投影，需要把视椎体投影到屏幕空间(screen space)，最后会得到像素位置。

将顶点从裁剪空间投影到屏幕空间，来生成2D坐标。

第一步，需要进行齐次除法(homogeneous diision)，就是把齐次坐标系中的x,y,z分量除以w，在OpenGL中这一步得到的坐标也被称为归一化的设备坐标(Normalized Device Coordinated, NDC).

在OpenGL里，x，y，z的取值范围是[-1, 1]

在DirectX里，x，y的取值范围是[-1, 1]，z的取值范围是[0, 1]，如果定义了UNITY_REVERSED_Z，则z的范围在[1, 0],  越靠近屏幕，z越大

深度：

即depth buffer里面的值，则是用此时的z通过线性映射到[0, 1]中，如果定义了UNITY_REVERSED_Z,则是映射到[1, 0]，越靠近屏幕深度越大。

第二步，映射过程，在Unity中，屏幕左下角是(0,0)，右上角是(pixelWidth,pixelHeight)，由于立方体内的坐标都是[-1,1]，因此映射过程就是一个缩放的过程。

齐次除法和屏幕映射可以总结为下面的公式：

 

 

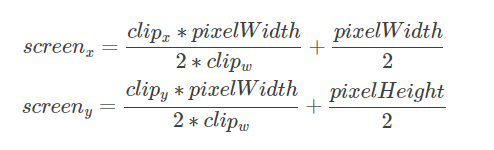
此外，从裁剪空间到屏幕空间的转换是由底层帮我们完成的，如在屏幕后处理等情况中需要用到，则可调用ComputeScreenPos函数：https://blog.csdn.net/zengjunjie59/article/details/111144851

需要注意的是ComputeScreenPos如果在顶点着色器中调用，那么结果只能在顶点着色器中使用，因为经过插值之后传到片元着色器中的时候数值有错误，之所以错误是因为转换第一步中的透视除法导致NDC下的坐标Np = {Nx, Ny, Nz}中的Nx与裁剪坐标Vp中的Vz不是线性关系了。因为Nz = -b / Vz - a，设Ny不变，当投影后的Nx均匀改变的时候Vz并不是均匀改变的（导数不是常数），如果把Nx与Vz当作线性相关的进行插值求得深度Vz会是错误的，应该是一条曲线。