《Real Time Rendering 4th》9.5 章读书笔记

经典的折射和反射定律

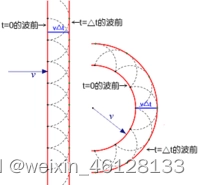
光通过两个不同介质的界面的时候，会发生反射和折射现象。反射是指光从另一个路径离开界面，折射是指光通过界面进入了另一种介质中。其中满足条件：

1. 反射角等于入射角
2. 折射角与入射角满足斯涅尔定律

$$\frac{sin{\theta }_1}{sin{\theta }_2}=\frac{n2}{n1}$$

其中 n1, n2 是两个介质的折射率

菲涅尔公式

入射光的电场振动方向可以取与光的传播方向垂直的任意方向。我们可以将电矢量分解为与光的入射面（入射界面法线与光线构成的面）垂直和平行的两个分量，并分别记为 Es （垂直）和 Ep （平行）。

根据电磁场的边值关系我们可以得到关于这两个分矢量在反射，折射中与入射时的比值关系：
$$\begin{array}{rl}{r}_s& =\frac{A_{1s}^{\prime }}{A_{1s}}=-\frac{sin({\theta }_1-{\theta }_2)}{sin({\theta }_1+{\theta }_2)}\\ & \\ t_s& =\frac{A_{2s}}{A_{1s}}=\frac{2sin{\theta }_{2}cos{\theta }_1}{sin({\theta }_1+{\theta }_2)}\\ & \\ r_p& =\frac{A_{1p}^{\prime }}{A_{1p}}=\frac{tan({\theta }_1-{\theta }_2)}{tan({\theta }_1+{\theta }_2)}\\ & \\ t_p& =\frac{A_{2p}}{A_{1p}}=\frac{2sin{\theta }_{2}cos{\theta }_1}{sin({\theta }_1+{\theta }_2)cos({\theta }_1-{\theta }_2)}\\ & \end{array}$$

其中：

• rs ：s 波的反射系数
• ts ：s 波的透射系数
• rp ：p 波的反射系数
• tp ：p 波的透射系数
• A ：对应电矢量的振幅

这四个公式合称 菲涅公式，它描述了两件事情：

1. 入射光的电矢量的两个分量，即 s 和 p 在发生反射和折射时，能量的再分布规律不同
2. 两个电矢量分量在发生反射和折射时，其振幅与入射时的振幅之比满足以上关系

当入射角很小的时候，有：
$$\begin{gathered} tan\theta \approx sin\theta \approx \theta \\ \frac{sin{\theta }_1}{sin{\theta }_2}\approx \frac{{\theta }_1}{{\theta }_2}\approx \frac{n2}{n1}=n \end{gathered}$$
于是得到菲涅尔公式在接近垂直入射的情况下的近似公式：
$$\begin{array}{rl}{r}_s& =-\frac{n-1}{n+1}\\ & \\ t_s& =\frac{2}{n+1}\\ & \\ r_p& =\frac{n-1}{n+1}\\ & \\ t_p& =\frac{2}{n+1}\\ & \end{array}$$
根据菲涅尔公式可以得到一个很重要的物理结论，就是当入射光是从光疏介质进入光密介质（n1 < n2）时，在入射角很小的情况下会发生反射部分发生“半波损失”。但对渲染更重要的是关心反射光，透射光和入射光的能量占比，其中反射能量和入射能量的比值称为反射率，而透射部分与入射部分的能量比值称为透射率，这些都可以从菲涅尔公式推导出来的：

$$\begin{array}{rl}R& =\frac{A_1^{\prime 2}}{A_1^2}\\ & \\ T& =\frac{n2cos{\theta }_2}{n1cos{\theta }_1}\frac{A_2^2}{A_1^2}=n\cdot \frac{cos{\theta }_2}{cos{\theta }_1}\frac{A_2^2}{A_1^2}\end{array}$$
其中：

• R：反射率
• T：透射率

并且根据能量守恒定律有：
$$R+T=1$$

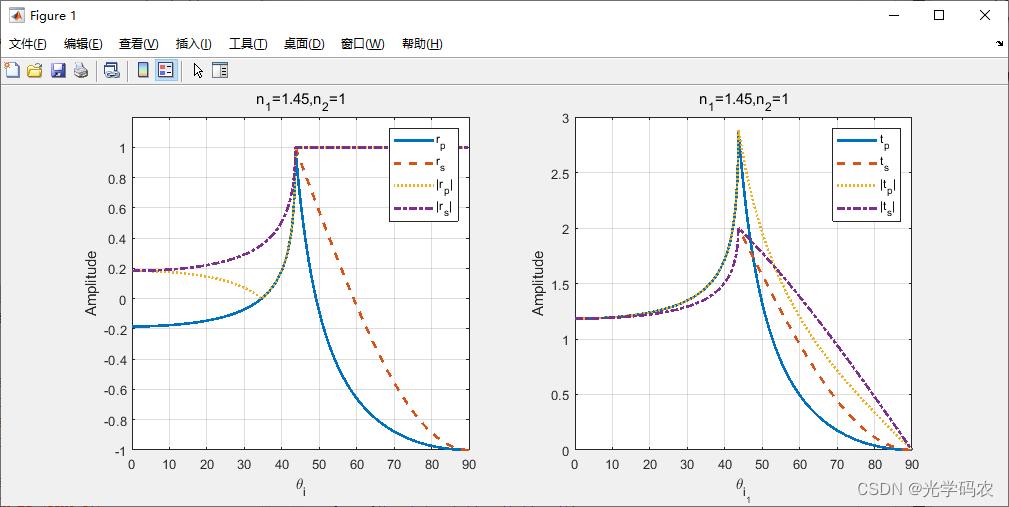
将菲涅公式带入反射率和透射率方程，可以得到 s 波和 p 波的反射率和透射率。

$$\begin{array}{rl}{R}_s& =\frac{A_{1s}^{\prime }}{A_{1s}}=\frac{si{n}^2({\theta }_1-{\theta }_2)}{si{n}^2({\theta }_1+{\theta }_2)}\\ & \\ T_s& =\frac{n_{2}cos{\theta }_2}{n1cos{\theta }_1}(\frac{A_{2s}}{A_{1s}}{)}^2=\frac{n2cos{\theta }_2}{n1cos{\theta }_1}\frac{4si{n}^2{\theta }_{2}co{s}^2{\theta }_1}{si{n}^2({\theta }_1+{\theta }_2)}\\ & \\ R_p& =\frac{A_{1p}^{\prime }}{A_{1p}}=\frac{ta{n}^2({\theta }_1-{\theta }_2)}{ta{n}^2({\theta }_1+{\theta }_2)}\\ & \\ T_p& =\frac{n_{2}cos{\theta }_2}{n1cos{\theta }_1}(\frac{A_{2p}}{A_{1p}}{)}^2=\frac{n2cos{\theta }_2}{n1cos{\theta }_1}\frac{4si{n}^2{\theta }_{2}co{s}^2{\theta }_1}{si{n}^2({\theta }_1+{\theta }_2)co{s}^2({\theta }_1-{\theta }_2)}\\ & \end{array}$$

两个波的反射率和透射率又分别满足能量守恒定律：
$$R_s+T_s=1,R_p+T_p=1$$

对于自然光，s 波和 p 波的能量相等，可以得到自然光的反射率：
$$\begin{array}{rl}{R}_n& =\frac{1}{2}(R_s+R_p)\\ & =\frac{1}{2}[\frac{si{n}^2({\theta }_1-{\theta }_2)}{si{n}^2({\theta }_1+{\theta }_2)}+\frac{ta{n}^2({\theta }_1-{\theta }_2)}{ta{n}^{(}{\theta }_1+{\theta }_2)}]\end{array}$$

当入射角很小的时候，有：
$$R_n=(\frac{n-1}{n+1}{)}^2$$

在《Real Time Rendering 4th》中，这个值被记作 F0，即接近0°入射角时的菲涅尔反射率。当入射角等于90°时，透射率为0，反射率为1。从0°增大到90°的过程中，反射率的变化规律随不同材料，不同波长的光而有所不同。

一个很有趣的事情是，对于不导电的介质而言，它的反射率变化几乎与光波无关，正如左下图所示。而对于良导体，例如金属而言，不同波长的光的反射率变化有较大区别，甚至不是单调的。这与金属的特性有关，即金属中存在大量的自由电子，且这些自由电子一般只分布在金属表面上。这些自由电子在表面层形成表层电流，而金属内部电荷体密度为0。

这两个性质影响着电磁场的边值关系，从而也影响着菲涅尔公式的推导。依赖新的边值关系我们可以得出只有当赋予金属一个复折射率才可以将绝缘介质中得到的折射和反射方程搬到金属这里来。然而，金属这个复折射率还依赖于光的频率，所以对于不同波长的光，它在金属表面的反射特性就表现得不同。也正是因为如此，在渲染中我们可以用一个数字为一个绝缘体指定反射率，但是需要三个数字（RGB）来为金属指定反射率。

上图分别描绘了从空气进入：玻璃，铜，铝三种材料的反射率变化规律。下图则截取了红绿蓝三原色的截面。可以看出，因为铜的红光反射率很高，所以铜表面呈现偏红的色泽，而铝对于不同波长的光的反射率区别比较小，所以表面呈白色/银色。

实际渲染中，我们无法直接计算这么负责的反射率方程，所以书中给出了简化的版本，同时考虑到人眼的透视效应，自变量从入射角折射角的θ，变成了法线 n 和 入射矢量 l：
$$F(\text{n},\text{l})\approx F_0+(1-F_0)(1-(\text{n},\text{l}{)}^{+}{)}^5$$

或者，还提出，在某些程序中会使用以下更通用的版本：
$$F(\text{n},\text{l})\approx F_0+(F_{90}-F_0)(1-(\text{n},\text{l}{)}^{+}{)}^{\frac{1}{p}}$$
这个式子不同的地方在于，F90 可以不为1，用来处理一些菲涅尔方程不能很好地进行描述的材料。