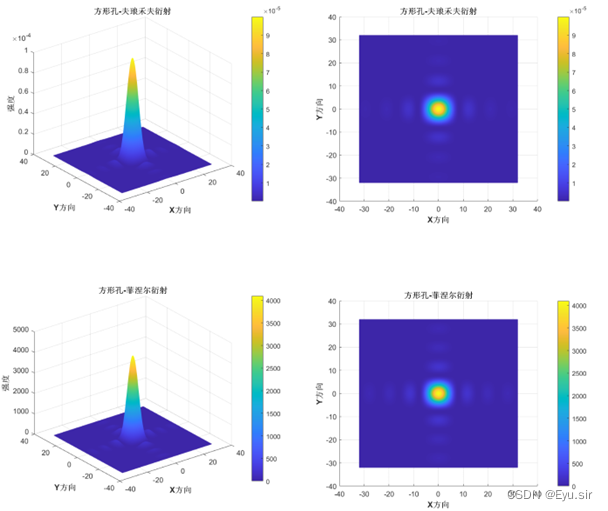
惠更斯-菲涅尔原理
惠更斯原理
球形波面上的每一点(面源)都是一个次级球面波的子波源,子波的波速与频率等于初级波的波速和频率,此后每一时刻的子波波面的包络就是该时刻总的波动的波面。其核心思想是:介质中任一处的波动状态是由各处的波动决定的。
光的直线传播、反射、折射等都能以此来进行较好的解释。此外,惠更斯原理还可解释晶体的双折射现象。但是,原始的惠更斯原理是比较粗糙的,用它不能解释衍射现象,而且由惠更斯原理还会导致有倒退波的存在,而这显然是不存在的。
由于惠更斯原理的次波假设不涉及波的时空周期特性——波长,振幅和相位,虽然能说明波在障碍物后面拐弯偏离直线传播的现象,但实际上,光的衍射现象要细微的多,例如还有明暗相间的条纹出现,表明各点的振幅大小不等,对此惠更斯原理就无能为力了。因此必须能够定量计算光所到达的空间范围内任何一点的振幅,才能更精确地解释衍射现象。
菲涅尔补充
菲涅耳在惠更斯原理的基础上,补充了描述次波的基本特征——相位和振幅的定量表示式,并增加了“次波相干叠加”的原理,从而发展成为惠更斯—菲涅耳原理。这个原理的内容表述如下:
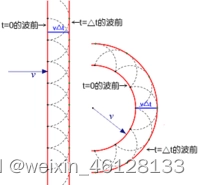
面积元dS所发出的各次波的振幅和相位满足下面四个假设:
(1)在波动理论中,波面是一个等相位面。因而可以认为dS面上各点所发出的所有次波都有相同的初相位(可令其为零)。
(2)次波在P点处所引起的振动的振幅与r成反比。 这相当于表明次波是球面波。
(3)从面元dS所发次波在P处的振幅正比于dS的面积,且与倾角θ有关,其中θ为dS的法线N与dS到P点的连线r之间的夹角,即从dS发出的次波到达P点时的振幅随θ的增大而减小(倾斜因数)。
(4)次波在P点处的相位,由光程nr决定。
基尔霍夫完善
惠更斯-菲涅耳原理不是严格的理论产物,较大程度上是凭朴素的直觉而得到的,对倾斜因子无法给出具体的函数形式 ,菲涅尔只对它作了某种猜测:θ=0时倾斜因子为1,θ=90时下降到零(即假定无后退次波)。后来古斯塔夫·罗伯特·基尔霍夫(Gustav Robert Kirchhoff)和阿诺德·索末菲(Arnold Johannes Wilhelm Sommerfeld)根据一般的波动理论从理论上导出了与菲涅耳的公式十分接近的衍射公式,同时还给出倾斜因子F(θ)的具体函数形式。