我以往在学习F分析的时候,编写了一个作业代码,在此附上供大家学习交流。
引言:
在傅里叶光学信息基础中,主要研究的是光在传播过程携带的信息如何去检测得到。如果光在自由空间(均匀介质)中的传播,那么光的性质(方向、频率)将不发生改变。我们易去得到它携带的信息,比如光强、频率。但是,当光在空间中遇到了障碍物(比如圆孔、矩形孔等),那么光的波动性将会显著表达。在接受屏上我们可以看到衍射现象,即光偏离原方向传播。在衍射现象中,我们一般分为夫琅禾夫衍射和菲涅尔衍射。从基尔霍夫衍射理论和角谱理论出发,实验现象和理论符合较好。针对圆孔和矩形孔,本文将用Matlab语言对夫琅禾夫衍射和菲涅尔衍射进行数值模拟。
理论:
(1)菲涅尔衍射公式:
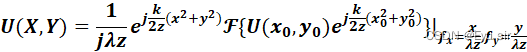
观察平面距离z条件:
![]()
(2)夫琅禾夫衍射公式:
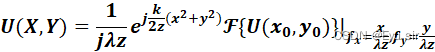
观察平面距离z条件:
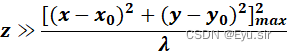
代码:
%% --------------------------------------------------------------------------%%
%% 清除空间
clear;
clc;
%% 夫琅禾夫衍射--圆孔
%% 三维--解析法
a=8.5*10^-2;%半径
lambda=632*10^(-9);%波长
z=a^(2)/lambda*100;%距离
N=16;%空间范围
L=512;%采样点
[x, y]=meshgrid(linspace(-N,N,L));%网格
p=sqrt(x.^2+y.^2);%每个点直接的距离
m=2*pi*a*p/z/lambda;%自变量
j1=besselj(1,m);%贝塞尔
i_0=(2*pi*a^(2)/(2*z*lambda))^2;%初始光强
i=i_0*(2*j1./m).^2;%透射光强
figure()%画图
mesh(x,y,i);%三维
zlabel('强度')
xlabel('X方向')
ylabel('Y方向')
title('圆孔-夫琅禾夫衍射')
grid on;%上色
colormap;%显色
colorbar;%颜色棒
%% 三维--快速傅里叶变换
figure()
z1=zeros(L,L);%透射空间
for i =1:L%在透射空间中画出圆形,圆形内部透射率为1for j =1:Lif x(i,j)^2+y(i,j)^2<=a%判断距离z1(i,j)=1;%透射率为1end end
end
d=fftshift(abs((fft2(z1)).^2));%快速傅里叶变换,并移动坐标为原点
mesh(x,y,d);%三维
zlabel('强度')
xlabel('X方向')
ylabel('Y方向')
title('圆孔-夫琅禾夫衍射')
grid on;%上色
colormap;%显色
colorbar;%颜色棒
%% 下面参数基本相同不做标记
%% 二维--解析法
figure()
p_1=-10:0.0001:10;
m_1=2*pi*a*p_1/z/lambda;
j1=besselj(1,m_1);
i_1=(2*j1./m_1).^2;
plot(m_1,i_1)
xlabel('离几何中心距离')
ylabel('强度')
title('圆孔-夫琅禾夫衍射')
%% 二维--快速傅里叶变换
figure()
p_1=linspace(-8,8,L);
d=fftshift(abs((fft2(z1)).^2));
plot(p_1,d(L/2,:))
xlabel('离几何中心距离')
ylabel('强度')
title('圆孔-夫琅禾夫衍射')
%% 菲涅尔衍射-圆孔
%% 三维--快速傅里叶变换
figure()
z=a^(2)*pi/4/lambda*100;
z1=zeros(L,L);
z2=zeros(L,L);
for i =1:Lfor j =1:Lif x(i,j)^2+y(i,j)^2<=az1(i,j)=1;z2(i,j)=x(i,j)^2+y(i,j)^2;end end
end
d=fftshift(abs((fft2(z1.*exp(1i*2*pi/lambda/2/z*z2))).^2));
i_2=d;
mesh(x,y,i_2);grid on;
zlabel('强度')
xlabel('X方向')
ylabel('Y方向')
title('圆孔-菲涅尔衍射')
colormap;
colorbar;
%% 二维--快速傅里叶变换
figure()
p_1=linspace(-8,8,L);
d=fftshift(abs((fft2(z1.*exp(1i*2*pi/lambda/2/z*z2))).^2));
plot(p_1,d(L/2,:))
xlabel('离几何中心距离')
ylabel('强度')
title('圆孔-菲涅尔衍射')
%% 夫琅禾夫衍射--方形孔
%% 三维--解析法
a=8.5*10^-2;
b=8.5*10^-2;
lambda=573.3*10^(-9);
N=32;L=1024;
z=a^(2)/lambda*100;
[x,y]=meshgrid(linspace(-N,N,L));
p1=x.*a/(lambda*z);p2=y.*b/(lambda*z);
i_0=(a*b/(lambda*z))^2;
i=i_0*(sinc(p1).^2).*(sinc(p2).^2);
figure()
mesh(x,y,i);grid on;
zlabel('强度')
xlabel('X方向')
ylabel('Y方向')
title('方形孔-夫琅禾夫衍射')
colormap;
colorbar;
%% 菲涅尔衍射-方形孔
%% 三维--快速傅里叶变换
a=2.25*10^-1;
b=2.25*10^-1;
lambda=573*10^(-9);
N=32;L=1024;
z=a^(2)*pi/4/lambda*500;
[x,y]=meshgrid(linspace(-N,N,L));
z1=zeros(L,L);
z2=zeros(L,L);
for i =1:Lfor j =1:Lif abs(x(i,j))<=a && abs(y(i,j))<=bz1(i,j)=1;z2(i,j)=x(i,j)^2+y(i,j)^2;end end
end
d=fftshift(abs((fft2(z1.*exp(1i*2*pi/lambda/2/z*z2))).^2));
figure()
mesh(x,y,d);grid on;
zlabel('强度')
xlabel('X方向')
ylabel('Y方向')
title('方形孔-菲涅尔衍射')
colormap;
colorbar;
%% --------------------------------------------------------------------------%%
运行结果中的一个:

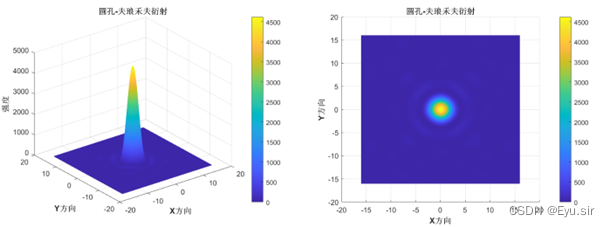
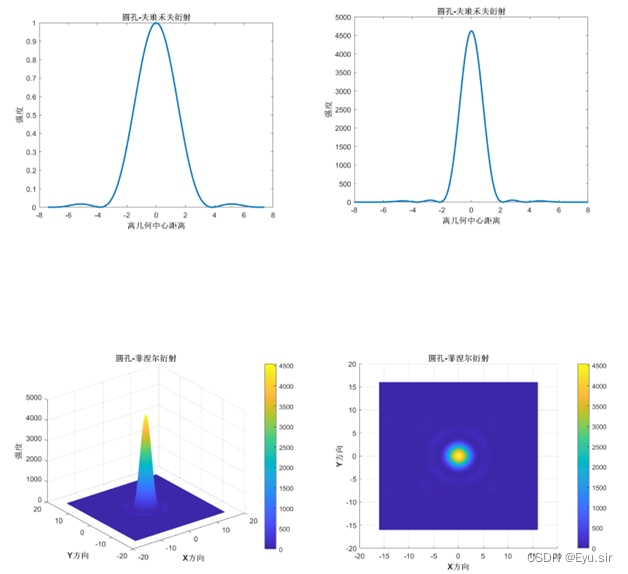
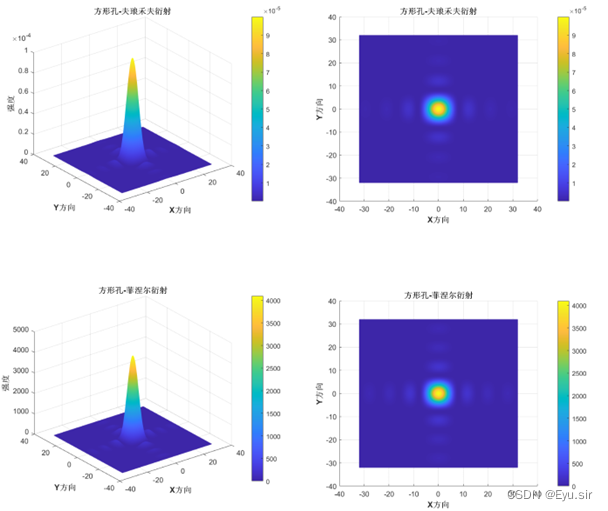
(凑字数)傅里叶光学的本质就是利用线性叠加的正交坐标函数集去表述一个复杂的函数,从而更简单地去处理复杂函数所带给我们的信息。而在实际应用上,由于器件的限制,我们通常做的就是利用离散的器件以及狄拉克函数性质去描述一个空间点的信息,然后相加求和去近似的描述原本连续的函数关系,也就是实际效果,比如单缝衍射等。简而言之,就是利用离散描述连续,是傅里叶方法应用在光学处理上的核心。
同时大家觉得有什么问题和建议欢迎留言。