二叉检索树（BST）

使用无序表和有序表组织的数据，不是查找时间复杂度偏高，就是插入时间复杂度偏高，而接下来将要介绍的二叉检索树（BST）则能很好的解决以上问题。二叉检索树又称二叉查找树、二叉排序树。

BST性质

BST是满足下面所给出条件的二叉树：

对于二叉检索树的任意一个结点，设其值为K，则该结点左子树中任意一个结点的值都小于K；该结点右子树中任意一个结点的值都大于或等于K。

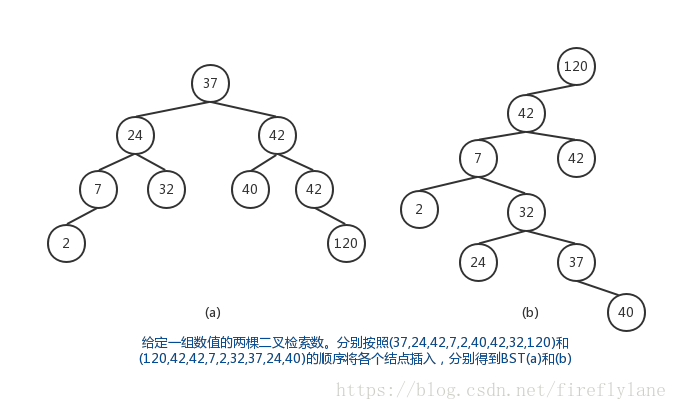
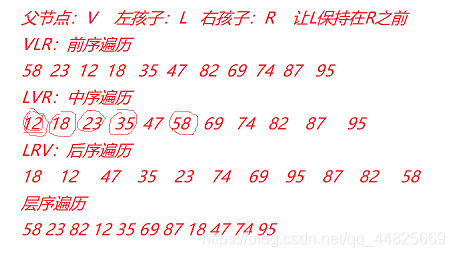
对于一组数，将这组数的两个排列按规则插入到BST中，如果采用中序遍历将各个结点打印出来，则会得到由小到大排列的相同序列。如下图

BST实现

template <typename Key, typename E>
class BST : public Dictionary<Key, E>
{
private:BSTNode<Key, E>* root;int nodecount;void clearhelp(BSTNode<Key, E>*);BSTNode<Key, E>* inserthelp(BSTNode<Key, E>*, const Key&, const E&);BSTNode<Key, E>* deletemin(BSTNode<Key, E>*);BSTNode<Key, E>* removehelp(BSTNode<Key, E>*, const Key&);E findhelp(BSTNode<Key, E>*, const Key&) const;void printhelp(BSTNode<Key, E>*, int) const;public:BST() { root = NULL; nodecount = 0; }~BST() { clearhelp(root); }void clear() { clearhelp(root); root = NULL; nodecount = 0; }void insert(const Key& k, const E& e){root = inserthelp(root, k, e);nodecount++;}E remove(const Key& k){E temp = findhelp(root, k);if(temp != NULL){root = removehelp(root, k); // 这里有点迷啊，已经找了一次，难道还要找一次？？？nodecount--;}return temp;}E removeAny(){if(root != NULL){E temp = root->element();root = removehelp(root, root->key());nodecount--;return temp;}else return NULL;}E find(const Key& k) const { return findhelp(root, k); }int size() { return nodecount; }void print() const{if(root == NULL) cout << "The BST is empty.\n";else printhelp(root, 0);}
};

注：本例中使用的类BSTNode和DictionaryADT的定义可以参见博主这两篇博文二叉树线性表(五) 字典

辅助函数

1.查找和插入

template <typename Key, typename E>
E BST<Key, E>::findhelp(BSTNode<Key, E>* root, const Key& k) const
{if(root == NULL) return NULL;if(k < root->key())return findhelp(root-left(), k);else if(k > root->key())return findhelp(root->right(), k);else return root->element();
}template <typename Key, typename E>
BSTNode<Key, E>* BST<Key, E>::inserthelp(BSTNode<Key, E>* root, const Key& k, const E& it)
{if(root == NULL)return new BSTNode<Key, E>(k, it, NULL, NULL);if(k < root->key())root->setLeft(inserthelp(root->left(), k, it));else root->setRight(inserthelp(root->right(), k , it));return root;
}

2.删除

template <typename Key, typename E>
BSTNode<Key, E>* BST<Key, E>:: deletemin(BSTNode<Key, E>* rt)
{if(rt->left() == NULL)return rt->right();else{rt->setLeft(deletemin(rt->left()));return it;}
}template <typename Key, typename E>
BSTNode<Key, E>* BST<Key, E>:: getmin(BSTNode<Key, E>* rt)
{if(rt->left() == NULL)return rt;else return getmin(rt->left());
}// remove
template <typename Key, typename E>
BSTNode<Key, E>* BST<Key, E>:: removehelp(BSTNode<Key, E>* rt, const Key& k)
{if(rt == NULL) return NULL;else if(k < rt->key())rt->setLeft(removehelp(rt->left(), k));else if(k > rt->key())rt->setRight(removehelp(rt->right(), k));else{BSTNode<Key, E>* temp = rt;if(rt->left() == NULL){rt = rt->right();delete temp;}else if(rt->right() == NULL){rt = rt->left();delete temp;}else{BSTNode<Key, E>* temp = getmin(rt->right());rt->setElement(temp->element());rt->setKey(temp->key());rt->setRight(deletemin(rt->right()));delete temp;}}return rt;
}

删除操作需要分类讨论，被删除的结点记为 rt：

如果 rt 的左子树为空，则只需缩短右侧的树链
如果 rt 的右子树为空，则只需缩短左侧的树链
如果 rt 左右子树均存在，这时我们需要考虑用一个原树中的一个元素替换 rt，以保证BST的性质不变

针对情况3，我们的解决方案是：使用 rt 右子树中的最小结点来替换 rt，这样能保证左子树的所有值都小于根结点，右子树的所有值都大于等于根结点。而我们可以通过getmin()很方便找到右子树中的最小结点。

下面再来讨论一下 rt->setLeft(deletemin(rt->left()));

看上去每次退出时都要将路径上的所有链重新赋值增加了时间复杂度，但实际上，不仅时间复杂度没有增加，这种做法给编程提供了极大的便利性：这里我们首先要建立一个观念，树的操作总是将cur指针指向根结点的，而子树的根结点虽然还有父结点，但是根结点并不知道自己还有父结点，因为由于树的递归定义，树的操作我们总是采用递归来实现，递归的过程就是通过树链上的“寻路”将我们的树的规模不断的缩小。

如果我们不在递归"出口处"将 rt 子树的左右结点进行修改，而是在删除结点的递归层进行修改的话，我们并不能知道被删除结点 rt 的父结点，而如果我们像单链表一样对于 rt 的定义进行修改的话，不但程序意图难以理解，而且还需要增加一些特殊情况的处理代码，百害而无一利。

注：removehelp对于递归返回值和递归出口处的操作的设计十分重要，值得去总结学习

3.清除和打印

// postorder
template <typename Key, typename E>
void BST<Key, E>:: clearhelp(BSTNode<Key, E>* root)
{if(root == NULL) return;clearhelp(root->left());clearhelp(root->right());delete root;
}// inorder
template <typename Key, typename E>
void BST<Key, E>:: printhelp(BSTNode<Key, E>* root, int level) const
{if(root == NULL) return;printhelp(root->left(), level+1);for(int i = 0; i < level; i++)cout << " ";cout << root->key() << "\n";printhelp(root->right(), level+1);
}