二分搜索树-BST，python实现

- 为什么要用二分搜索树
- 二分搜索树的定义
- 二叉搜索树的基本功能
  - 初始化二分搜索树的节点
  - 插入元素
  - 查找元素
  - 深度优先遍历
  - 广度优先遍历
  - 删除操作
    - 要删除的节点没有孩子节点
    - 要删除的节点有两个孩子节点
    - 要删除的节点有一个孩子节点
  - floor 和ceil操作

为什么要用二分搜索树？

二分搜索树最常用的场景就是查找表的实现，其实可以看成是字典的形式，这样的一对对数据，我们就可以通过键来直接查找到对应的值。进行相应的操作。你可能会想到，这样的key的值，可以直接用数组来存储，但很多时候，键值不一定都是整数，所以这时候实现一个二分搜索树就很明智了。

二分搜索树的优势在哪里呢？
比较一下使用三种方法实现这样一个查找表的时间复杂度

二分搜索树的效率是最高的，而且不仅仅是查找，插入，删除等也是非常高效的，因此，我们可以动态的维护数据，除此之外，还有很多业务上的操作二分查找树也能实现，比如min,max，floor,ceil等。

二分搜索树的定义

二分搜索树也是一颗二叉树，如图所示：

与一般的二叉树不同的是，二分搜索树树具有一下三个性质：

若左子树不为空，则左子树上所有节点的值均小于它的根节点的值
若右子树不为空，则右子树上所有节点的值均大于它的根节点的值
以左右孩子为根的子树依然是二分搜索树
没有键值相等的节点

在讲到堆的时候，我曾说堆是一颗完全的二叉树，但二分搜索树并没有这个限制，如下这样的二叉树也是二分搜索树：

因为不是完全的二叉树，所以我们不能再使用数组来存储相应的结构了，在二分搜索树中我们使用节点来存储相应的结构，主要的结构有：

key
value
parent
left:左孩子
right:右孩子

二叉搜索树的基本功能

初始化二分搜索树的节点

根据上一节说的二分搜索树的主要特点，我们需要设计一下初始化的函数，方便接下来的插入，删除等操作。

#创建树节点类
class TreeNode(object):def __init__(self,key,value,parent = None,left=None, right = None):#初始化self.key = keyself.value = valueself.leftChild = leftself.rightChild = rightself.parent = parentdef hasLeftChild(self):return self.leftChilddef hasRightChild(self):return self.rightChilddef isLeftChild(self):return self.parent and self.leftChild == selfdef isRightChild(self):return self.parent and self.rightChild == selfdef isRoot(self):return not self.parentdef isLeaf(self):return not (self.leftChild and self.rightChild)

插入元素

如图所示：

假如要插入一个元素60，比较一下待插入元素（60）和根节点的元素（41）的大小，如果60>41，则判断一下41这个当前节点是否有右孩子（维护性质），如果有，则把右孩子更新为当前节点，做一个递归的操作；如果没有，直接插入到41这个元素右孩子所在位置。
详见python代码：

class BST(object):def __init__(self):self.size = 0self.root = Nonedef __len__(self):return self.sizedef length(self):return self.sizedef insert(self,key,value):if self.root:self._insert(key,value,self.root)else:self.root = TreeNode(key,value)self.size += 1return self.rootdef _insert(self,key,value,currentNode):if key < currentNode.key:if currentNode.hasLeftChild():self._insert(key,value,currentNode.leftChild)else:currentNode.leftChild = TreeNode(key,value,parent=currentNode)elif key == currentNode.key:currentNode.value = valueelse:if currentNode.hasRightChild():self._insert(key,value,currentNode.rightChild)else:currentNode.rightChild = TreeNode(key,value,parent=currentNode)def __setitem__(self, key, value):self.insert(key,value)

查找元素

比较一下42>41，所以在41的右子树中寻找
42<58,所以在58的左子树中找
42<50，在左子树中找，
找到42,如果没有，就证明没有这个对应的元素

这里写图片描述

    def get(self,key):if self.root:res = self._get(key,self.root)if res:return res.valueelse:return Noneelse:return Nonedef _get(self,key,currentNode):if currentNode is None:return Noneelif key == currentNode.key:return currentNodeelif key > currentNode.key:return self._get(key,currentNode.rightChild)else:return self._get(key,currentNode.leftChild)def __getitem__(self, item):return self.get(item)def __contains__(self, item):#查看待查找的元素中是否包含这样的键值if self._get(item,self.root):#get method returns a valuereturn Trueelse:return False
tree=BST()
tree.insert(1,'dd')
tree.insert(2,'d')
tree.insert(3,'dde')
tree.insert(4,'fafa')
value = tree.get(4)
print(value)

输出：

fafa

深度优先遍历

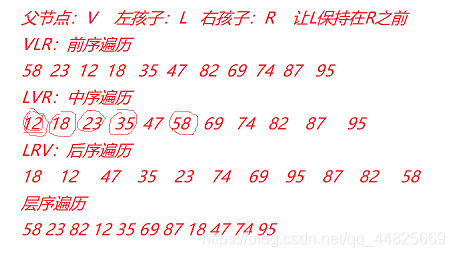
二分搜索树中的深度优先遍历分为前，中，后序遍历，他们的区别如下：

前序遍历先访问当前节点，然后依次递归的访问左右子树
中序遍历先递归访问左子树，再访问自身，然后递归访问右子树
后序遍历先递归访问左右子树，再访问自身

提供一种理解前中后序的方法，下面这一个节点分别三个小点，分别代表前，中，后。每次遍历，一个点要经过三次，如果是前序遍历，经过“前“对应的点时，把这个点打印出来。

如图是前序遍历时，打印的两个状态，第一幅图打印的顺序为： $28\rightarrow16\rightarrow13\rightarrow13\rightarrow13\rightarrow16\rightarrow22$ ，即当遍历的时候，只有到代表“前“那个小红点时才打印该节点。中序和后序类似。

总的来说，前序遍历就是当遍历到代表“前“那个节点时，才打印出来。

中序遍历打印的结果是从小到大排列的，如果想要对元素排序也可以使用中序遍历。

后序遍历：

def preOrder(self):#前序遍历self._preOrder(self.root)def _preOrder(self,treeNode):print(treeNode.key)self._preOrder(treeNode.leftChild)self._preOrder(treeNode.rightChild)def inOrder(self):#中序遍历self._inOrder(self.root)def _inOrder(self,treeNode):self._inOrder(treeNode.leftChild)print(treeNode.key)self._inOrder(treeNode.rightChild)def postOrder(self):#后序遍历self._postOrder(self.root)def _postOrder(self,treeNode):self._postOrder(treeNode.leftChild)self._postOrder(treeNode.rightChild)print(treeNode.key)

总结一下，注意print出现的位置。这种方式成为深度优先遍历。

广度优先遍历

广度优先遍历体现在二叉树中表示为层序遍历。按层来一层一层遍历完。如图：
这里写图片描述
通过队列的形式，先进先出，当遍历到28时，28出队进行相应的操作，然后让28的左右子节点入队，让左子节点16先出队，同时让左子节点（26）的左右子节点入队。然后才是30出队，让30的左右子节点入队。这样的出队顺序如下：

    def levelOrder(self):q = queue.Queue()q.put(self.root)while not q.empty():treeNode = q.get()print(treeNode.key)if treeNode.leftChild:q.put(treeNode.leftChild)if treeNode.rightChild:q.put(treeNode.rightChild)

删除操作

删除操作是二分搜索树中最难的部分，搞懂了这个，基本就能搞懂整个二分搜索树了。
删除操作的主要部分是remove函数，分为三种情况：

压迫删除的节点没有孩子
要删除的孩子有一个孩子
要删除的节点有两个孩子节点

我们分别来讨论这三种情况。

要删除的节点没有孩子节点

如图所示，如果没有孩子节点，意味着该节点为叶子结点，这是只需要把该节点删除即可。
这里写图片描述

要删除的节点有两个孩子节点

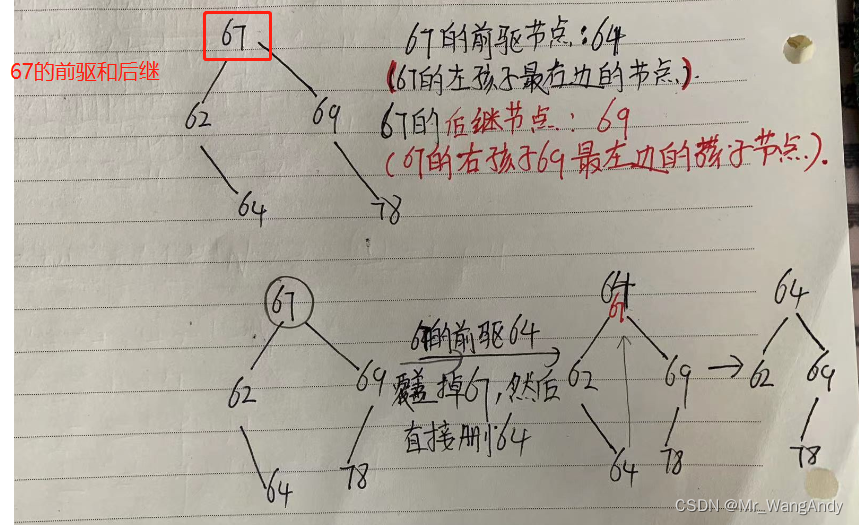
这种是最复杂的一种，我们要满足树的性质的同时，把这个节点删除，因此，就要找一个节点替代要删除节点的位置。

如图，假设要删除的节点为5这个节点，为了找到它的替代者，我们要两种方案可以选择：

选择以5的左孩子为根节点的子树中的最大值。（沿着2的右子树查找到尽头）
选择以5的右孩子为=根节点的子树中的最小值（7）。（沿着11的左子树找到尽头）

这里写图片描述
找到5的继承者7之后，还要把7这个位置完美得连接上。如图，7这个位置可能出现得情况有两种：7是叶子结点或者7有一个孩子。（不可能有两个孩子，如果7有两个孩子，它一定不是这个子树中的最值）。如果7是叶子节点就很好办，直接删除就可以了；如果7有一个孩子，也会出现两种情况，如图：

7有左孩子，这是需要处理的是（1），（2）。（不可能出现（3），即7不可能是根节点）
7有右孩子，需要处理（4），（5）两种情况。

这里写图片描述

处理好7的前后左右之后，再把7放到5的位置就OK了。

要删除的节点有一个孩子节点

这里写图片描述
如上图，直接将孩子节点放到要删除的节点的位置即可。但这里还需注意的是，要删除的节点的孩子节点可能出现两种情况：

有左孩子，需要处理（1），（2），（3）（要删除的节点可能为根节点）
有右孩子，需要处理（4），（5），（6）。

这里写图片描述
致辞就完成了删除操作。python主代码如下：

    def delete(self,key):if self.size > 1:nodeToRemove = self._get(key,self.root) if nodeToRemove:self.remove(nodeToRemove)self.size = self.size - 1else:raise KeyError("Error,key not in the tree")elif self.size ==1 and self.root.key == key:self.root = Noneself.size = self.size - 1else:raise  KeyError("Error,key not in the tree")def __delitem__(self, key):self.delete(key)def remove(self,currentNode):#help with method of deleteif currentNode.isLeaf():#the first case,no childrenif currentNode == currentNode.parent.leftChild:currentNode.parent.leftChild = Noneelse:currentNode.parent.rightChild = Noneelif currentNode.hasBothChildren():#the second case,has two childrensucc = currentNode.findSuccessor()succ.spliceOut() #splice the successor's child and parentcurrentNode.key = succ.keycurrentNode.value = succ.valueelse:#the third case,only one childrenif currentNode.hasLeftChild():if currentNode.isLeftChild():currentNode.leftChild.parent = currentNode.parentcurrentNode.parent.leftChild = currentNode.leftChildelif currentNode.isRightChild():currentNode.leftChild.parent = currentNode.parentcurrentNode.parent.rightChild = currentNode.leftChildelse: #currentNode is rootcurrentNode.replaceNodeData(currentNode.leftChild.key,currentNode.leftChild.payload,currentNode.leftChild.leftChild,currentNode.leftChild.rightChild)else:if currentNode.isLeftChild():currentNode.parent.leftChild = currentNode.rightChildcurrentNode.rightChild.parent = currentNode.parentelif currentNode.isrightChild():currentNode.parent.rightChild = currentNode.rightChildcurrentNode.rightchild.parent = currentNode.parentelse: #current is rootcurrentNode.replaceNodeData(currentNode.rightChild.key,currentNode.rightChild.payload,currentNode.rightChild.leftChild,currentNode.rightChild.rightChild)

同时函数中用到的辅助函数，需要添加到TreeNode类中。

def findSuccessor(self):#find the right subtree of minimumcurrent = self.rightChildwhile current.hasLeftChild():current = current.leftChildreturn currentdef spliceOut(self):#just a helper for Hubbard deletion for deleting itself,#like remove method of two cases(is leaf and has only one child)#the code is also similar with remove methodif self.isLeaf():if self.isLeftChild():self.parent.leftChild = Noneelse:self.parent.rightChild = Noneelif self.hasAnyChildren():if self.hasLeftChild():if self.isLeftChild():self.parent.leftChild = self.leftChildelse:self.parent.rightChild = self.leftChildself.leftChild.parent = self.parentelse:if self.isLeftChild():self.parent.leftChild = self.rightChildelse:self.parent.rightChild = self.rightChildself.rightChild.parent = self.parentdef replaceNodeData(self,key,value,lc,rc):#deal whth the current node is rootself.key = keyself.payload = valueself.leftChild = lcself.rightChild = rcif self.hasLeftChild():self.leftChild.parent = selfif self.hasRightChild():self.rightChild.parent = self

floor 和ceil操作

floor:给定一个key，寻找比key小，但在所有比key小的元素中的最大值
ceil：给定一个key，寻找比key大，但在所有比key大的元素中的最小值

如图所示，45的floor是42，ceil是50

这里写图片描述

    def getFloorAndCeil(self,key):#given the key,get the floor that is less than the key;get the ceil that is greater than the keyreturn self._getFloorAndCeil(key,self.root)def _getFloorAndCeil(self,key,currentNode,floor=None,ceil=None):if currentNode:if currentNode.key == key:floor,ceil = key,keyreturn floor,ceilelse:if currentNode.key < key: #沿着右子树继续找floor = currentNode.keyreturn self._getFloorAndCeil(key,currentNode.rightChild,floor,ceil)else:#沿着左子树找ceil = currentNode.keyreturn self._getFloorAndCeil(key,currentNode.leftChild,floor,ceil)else:return floor,ceil