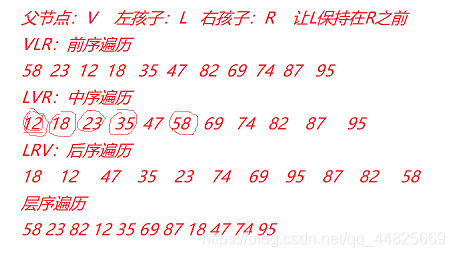
using System;
using 所以;
using System.Collections.Generic;
//想用list必须有他！！！
/*1．	设计BST 的左右链存储结构，并实现BST插入（建立）、删除、查找和排序算法。
2．	实现折半查找算法。
3．	实验比较：设计并产生实验测试数据，考察比较两种查找方法的时间性能，并与理论结果进行比较。以下具体做法可作为参考：
（1）	第1组测试数据： n=1024个已排序的整数序列（如0至2048之间的奇数）；第2组测试数据：第1组测试数据的随机序列。                                                                                                                                                                                                                                                                                            
（2）	按上述两组序列的顺序作为输入顺序，分别建立BST。（3）	编写程序计算所建的两棵BST的查找成功和查找失败的平均查找长度（主要是改造Search算法，对“比较”进行计数），并与理论结果比较。
（4）	以上述BST的中序遍历序列作为折半查找的输入，编写程序分别计算折半查找的查找成功和查找失败的平均查找长度，并与理论结果比较。（5）	以上实验能否说明：就平均性能而言，BST的查找与折半查找差不多，为什么？*///笔记！！！//List<int> scoreList = new List<int>();//int列表的使用!!!//scoreList.Add(tmp);//列表在这里的用法！！！Add给列表中的新元素赋值！！！不能直接用等号赋值！！！
namespace BST
{class Program{static void Main(string[] args){int i;int tmp;List<int> scoreList = new List<int>();//int列表的使用Tree Data = new Tree();Tree Data1 = new Tree();Tree Datatmp = new Tree();Console.WriteLine("1024个数的BST树的中序输出");for (i = 0; i < 1024; i++){Data.Add(i,i);}Data.Print1();Console.WriteLine("1024个数的查找的平均查找长度计算");for (i = 0; i < 1024; i++){Data.Search(i);}Data.Printcishu();//对于1024个数字的查找和构建以及输出已经结束for (i = 0; i < 10; i++){Random rd = new Random();tmp = rd.Next(0, 100);scoreList.Add(tmp);//列表在这里的用法！！！Add给列表中的新元素赋值！！！不能直接用等号赋值！！！Data1.Add(tmp, tmp);}Console.WriteLine("生成10个随机数的BST树的中序输出");Data1.Print1();Console.WriteLine("10个随机数的查找的平均查找长度计算");for (i = 0; i < 10; i++){Data1.Search(scoreList[i]);}Data1.Printcishu();//Random rd1 = new Random();//tmp = rd1.Next(0, 100);//Console.WriteLine(tmp);//Data.PrintLevelOrder();Console.ReadKey();}}
}

using System;
using System.Collections.Generic;
//System.Collections.Generic 命名空间包含定义泛型集合的接口和类，
//用户可以使用泛型集合来创建强类型集合，
//这种集合能提供比非泛型强类型集合更好的类型安全性和性能。namespace 所以
{class Tree{int cishu = 0;public class TreeNode{public int Data;//用来决定树的形状public int number;public TreeNode Left;//字段“成员变量”，一般在类的内部做数据交互使用。public TreeNode Right;//就是TreeNode.Right的意思//data left right都是treenode中的私有元素//下面的东西是一个元素public TreeNode(int Dta, int numb)//TreeNode.TreeNode(int Dta)是一个TreeNode里的函数{this.Data = Dta;//this可用于限定类似名称隐藏的成员//eg   this.name = name;//将对象作为参数传递给方法，例如：//CalcTax(this);this.number = numb;this.Left = null;//this代表treenodethis.Right = null;}public TreeNode AddNode(TreeNode Root, TreeNode NewNode)//引入两个treenode格式变量//表示TreeNode.AddNode函数{if (Root == null){Root = NewNode;return Root;}else if (Root.Data > NewNode.Data)//上面的用法！引用root这个treenode类中的public int data 元素{Root.Left = AddNode(Root.Left, NewNode);//给左节点赋值}else{Root.Right = AddNode(Root.Right, NewNode);}return Root;}}private TreeNode Root = null;public void Add(int Data, int number){TreeNode newNodeObj = new TreeNode(Data, number);Root = newNodeObj.AddNode(Root, newNodeObj);}//先序列遍private void Print(TreeNode Root){if (Root == null){return;}else{// Console.WriteLine(Root.Data);//输出的是字符串，所以用它也可以Console.WriteLine(Root.number);Print(Root.Left);//自己写的函数，遍历左子树Print(Root.Right);}}//中序遍历public void Print1(){InOrder(Root);//在这个print中运行的是带参数的print，细心！！！}public void InOrder(TreeNode Root){if (Root == null){return;;}else{{InOrder(Root.Left);// Console.WriteLine(Root.Data);Console.WriteLine(Root.number);InOrder(Root.Right);}}}public void Print2(){PostOrder(Root);//在这个print中运行的是带参数的print，细心！！！}//后序遍历public void PostOrder(TreeNode Root){if (Root == null){return;}else{PostOrder(Root.Left);PostOrder(Root.Right);// Console.WriteLine(Root.Data);Console.WriteLine(Root.number);}}public void Print(){Print(Root);//在这个print中运行的是带参数的print，细心！！！}public void Printcishu(){Console.WriteLine("本次查找的平均查找长度如下");Console.WriteLine(cishu);}public void PrintLevelOrder()//层序遍历{int i;int j;int flag;flag = 0;i = 0;j = 0;List<TreeNode> Data = new List<TreeNode>();//列表形元素Data.Add(Root);//在其中新增元素while (Data.Count != 0){TreeNode temp = Data[0];//tmp取代了data[0]Data.RemoveAt(0);//删除data[0]的意思Console.WriteLine($"编号为{temp.number % 100}的元素优先度为{temp.number / 10}");if (temp.Left != null){Data.Add(temp.Left);i = i + 1;}j = j + 1;if (temp.Right != null){Data.Add(temp.Right);i = i + 1;}j = j + 1;if ((i != j) && ((i == 6))){flag = 1;}}}public void Search(int FindIt){SearchIt(Root, FindIt);}private void SearchIt(TreeNode Root, int FindIt){cishu = cishu + 1;if (Root == null){Console.WriteLine("Not Found!!");return;}else if (FindIt == Root.Data){Console.WriteLine("Found!!");Console.WriteLine("该节点中存储的值分别为：");Console.WriteLine(Root.Data);Console.WriteLine(Root.number);return;}else if (FindIt > Root.Data){SearchIt(Root.Right, FindIt);}else if (FindIt < Root.Data){SearchIt(Root.Left, FindIt);}return;}}}