二、栈和队列

栈——后进先出

应用：数制转换、括号匹配、行编辑程序、迷宫求解、表达式求值、八皇后问题、函数调用、递归调用的实现

队列——先进先出

应用：脱机打印输出

多用户系统用户排队分时循环使用CPU和主存

按用户优先级排队，每个优先级一个队列

实时控制系统，信号按接受顺序依次处理

网络电文传输，按到达的时间先后顺序依次进行

2.1 栈

1.定义及特点

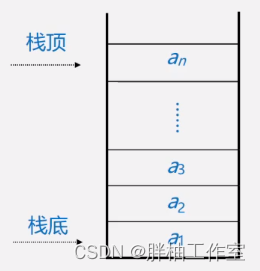
限定只能在表的一端进行插入和删除运算的线性表（只能在栈顶操作），后进先出(Last In First Out)，简称LIFO

表尾叫栈顶 Top
表头叫栈底 Base 或 Bottom

存储结构：顺序栈或链栈，以顺序栈更为常见

栈通常用 S 表示（stack）
插入元素到栈顶，称为入栈或压栈 PUSH(x)
从栈顶删除最后一个元素，称为出栈或弹栈 POP(x)
在这里插入图片描述

2、栈的表示与操作实现

首先设top指针指向栈顶元素之上的下标地址

另设base指针，指向栈底元素的位置

另外可以用stacksize表示栈可以使用的最大容量

顺序栈的操作：
base == top是栈空的表现

栈满了top - base == stacksize

栈满还加元素的处理方法：
1.报错，返回操作系统（√）
2.分配更大空间（麻烦）

上溢（overflow）：栈满还要加元素
下溢（underflow）：栈空了还要弹出元素

注：上溢是一种错误，使问题的处理无法进行，但是下溢一般认为是一种结束条件，即问题处理结束

#define MAXSIZE 100
#define OVERFLOW -2
#define OK 1
#define ERROR 0
typedef struct {SElemType *base;//栈底指针SElemType *top; //栈顶指针int stacksize;  //栈可用的最大容量
} SqStack;算法1：顺序栈的初始化
Status InitStack(SqStack &S) {	//构造空栈 S.base = new SElemType[MAXSIZE];//栈底指针指向一片连续的空间//或S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType));if (!S.base) exit (OVERFLOW);//空间分配失败//注：exit函数的头文件在#include <stdlib.h>S.top = S.base;//栈顶指针等于栈底指针（指向栈底）S.stacksize = MAXSIZE;//stacksize是栈的最大容量return OK;
}算法2：判断顺序栈是否为空
Status StackEmpty(SqStack S) {//若栈为空,返回TRUE;否则返回 FALSE if (S.top == S.base) return TRUE;//top指针和base重合else return FALSE;
} 算法3：求栈的长度
int StackLength(SqStack S) {return S.top - S.base;
}算法4：清空顺序栈
Status ClearStack(SqStack &S) {//不一定要把内存置为空，只要把它当成空就行if (S.base) S.top = S.base;//前提是栈要存在return OK;
}算法5：销毁顺序栈
Status DestroyStack( SqStack &S) {if (S.base) {delete S.base; 
//delete释放了内存空间，但是没有销毁指针，base指针成了野指针，所以还需要指向空S.stacksize = 0; S.base = S.top = NULL;}return OK. 
}算法6：顺序栈的入栈
Status Push(SqStack &S, SElemType e) {if (S.top-S.base == S.stacksize) return ERROR;//栈满了加不了了*S.top = e;++S.top; return OK;
}算法7：顺序栈的出栈
Status Pop(SqStack &S, SElemType &e) {//若栈非空，则删除S的栈顶元素，用e返回其值，并返回OK；否则返回ERRORif (S.top == S.base) return ERROR;//等价于if (StackEmpty(S))--S.top;e = *S.top;return OK;
}

2.2 队列

1.定义及特点

只能在表的一端进行插入，在表的另一端进行删除运算的线性表，先进先出（First In First Out），简称FIFO.
只能在队头和队尾运算（头删尾插）。

队列通常用Q表示（queue）
存储结构：顺序队或链队，以循环顺序队列更常见

案例引入

1、进制转换
把十进制159转换为八进制，倒序取余数可以用栈来进行
在这里插入图片描述

2、括号匹配
假设有两种括号（）[]

它们的嵌套顺序任意，即是：

1.() 或者[([][])] 是正确格式；

2.[(]) 为错错误格式;

3.([()) 或 (()]) 是错误格式。

利用栈的特点将左括号和右括号进行匹配，左括号入栈，右括号进行匹配，匹配则出栈，不匹配break，一下是几种不匹配的情况：

当遇到某一个右括号时，栈已空，说明目前为止，右括号多于左括号

从栈弹出的左括号与当前检验的右括号类型不同，说明出现了括号交叉

算术表达式输入完毕，但栈中还没有匹配的左括号，说明左括号多于右括号

3、表达式求值
表达式的组成：

操作数(operand)：常数、变量

运算符(operator)：算术运算符、关系运算符和逻辑运算符

界限符(delimiter)：左右括号和表达式结束符，如‘#’

例如：#3*(7-2)#

为了求解这样一个表达式就要两个栈一个是算符栈OPTR，一个是操作数栈OPND。前者存放运算符，另一个存运算结果。

从左到右扫描表达式，如果遇到运算数就放入OPND，如果是运算符，如果该运算符比OPTR的栈顶优先级高，则入栈OPTR，继续向后处理；否则从OPND中弹出两个运算数，从OPTR中弹出栈顶运算符进行运算，将结果压入OPND。如此向后处理，直到碰到结束符。

4、舞伴问题
假设在舞会上,男士和女士各自排成一队。舞会开始时, 依次从男队和女队的队头各出一人配成伴如果两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求写一算法模拟上述舞伴配对问题。

这题显然用队列解，分别构造男女两个队列来解决问题