1 研究背景

倒立摆是一个开环不稳定的强非线性系统，其控制策略与杂技运动员顶杆平衡表演的技巧有异曲同工之处，目的在于使得摆杆处于临界稳定状态，是进行控制理论研究的典型实验平台。20世纪50年代，麻省理工学院的控制论专家根据火箭助推器原理设计出了第一套倒立摆实验设备，开启了最初的相关研究工作。倒立摆的种类丰富多样，按照其结构可将其分为：直线倒立摆、环形倒立摆以及平面倒立摆等，按照摆杆级数又可将其分为：一级、二级甚至三级等。

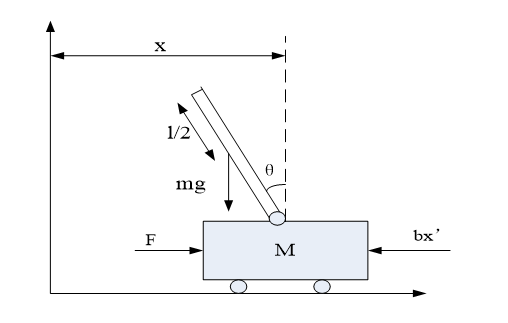
图1 直线一级倒立摆原理

按照工作原理可将现有的直线一级倒立摆实验装置抽象成小车和摆杆组成的系统，其中小车可沿固定导轨左右移动，摆杆可绕小车与摆杆之间的铰接点自由转动，如图1所示。控制系统依据读取到的小车位置以及摆杆角度信号，通过控制作用在小车上的水平力，使其沿固定导轨左右移动，可以使得摆杆始终处于垂直向上这样一个临界稳定位置，实验装置具体参数如表1所示。

2 模型推导

设N和P为小车与摆杆相互作用力的水平和垂直方向的分量。

图2 小车受力分析图

下面N和P为小车与摆杆相互作用力的水平和垂直方向的分量。

3 现代控制理论分析

3.1 状态空间方程

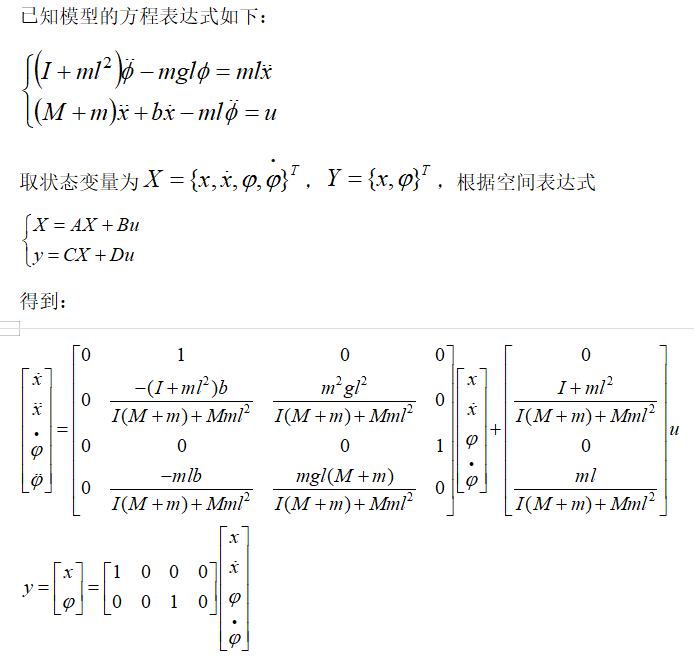
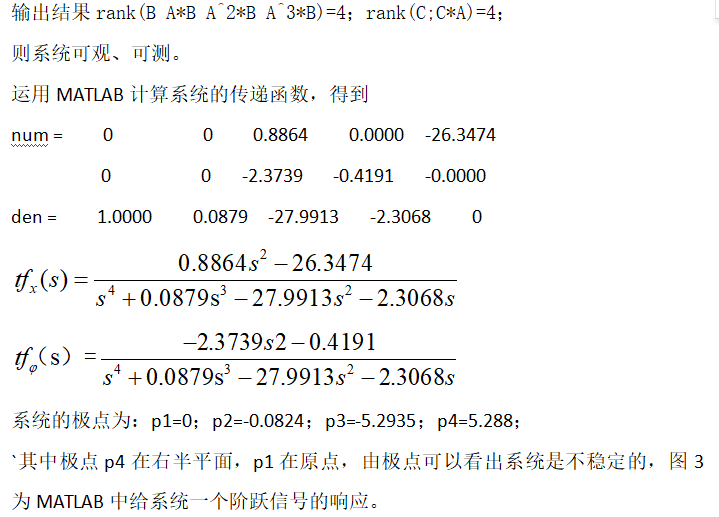
3.2 能控性和能观性

在MATLAB中进行计算，代码如下：

A=[0 1 0 0;0 -0.0883 0.6293 0;0 0 0 1;0 -0.2357 27.8285 0];B=[0;0.8832;0;2.3566];C=[1 0 0 0;0 0 1 0];control=[B A*B A^2*B A^3*B];disp('可控性矩阵的秩：')disp(rank(control))observe=[C;C*A];disp('可观性矩阵的秩：')disp(rank(observe))

3.3 状态反馈

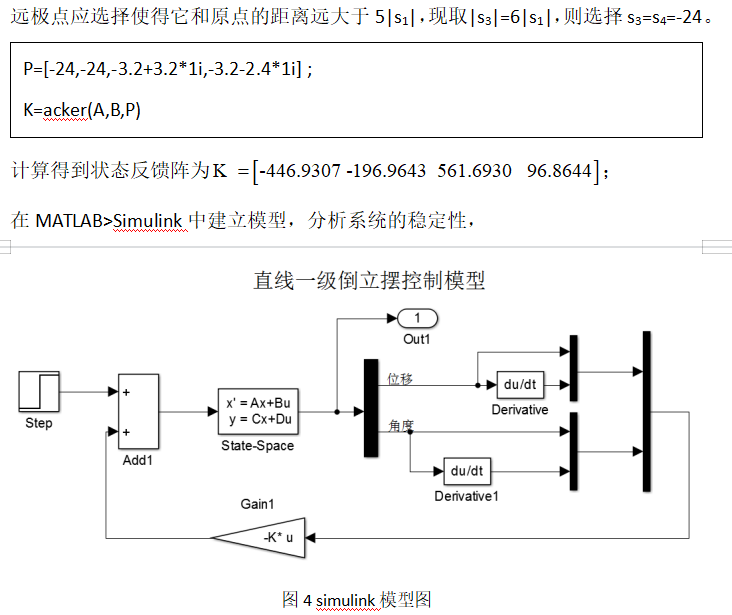
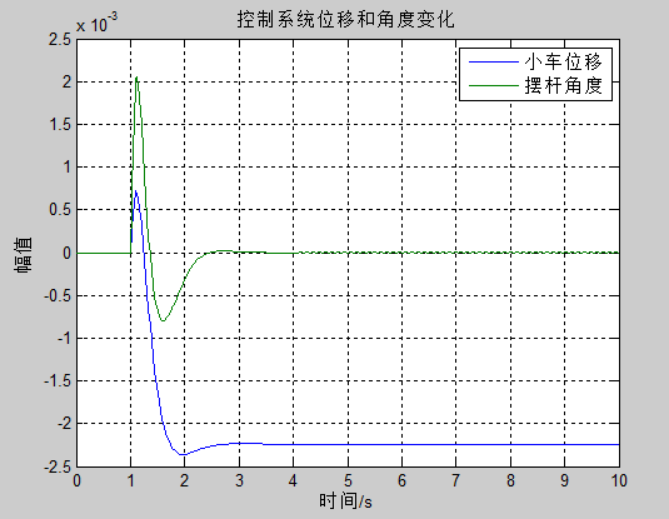
3.4 状态观测器

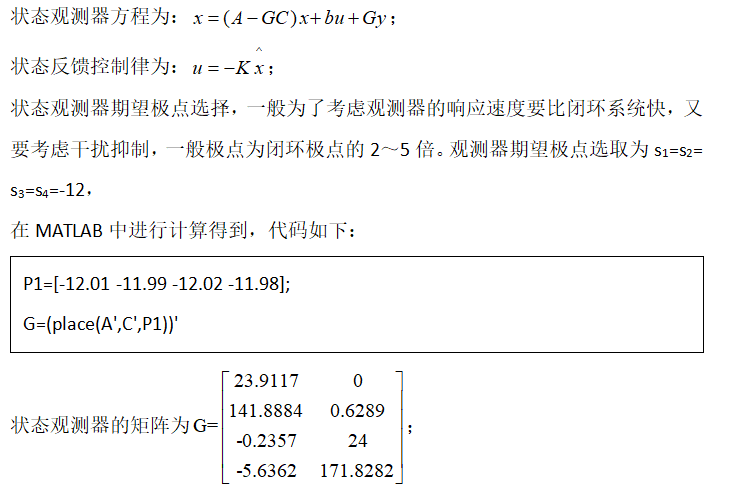
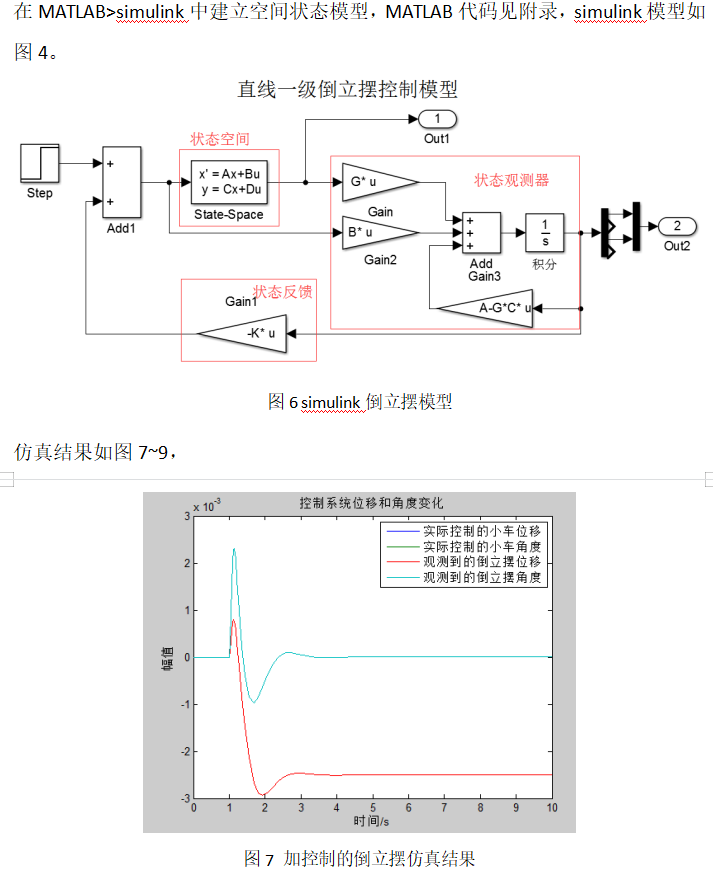
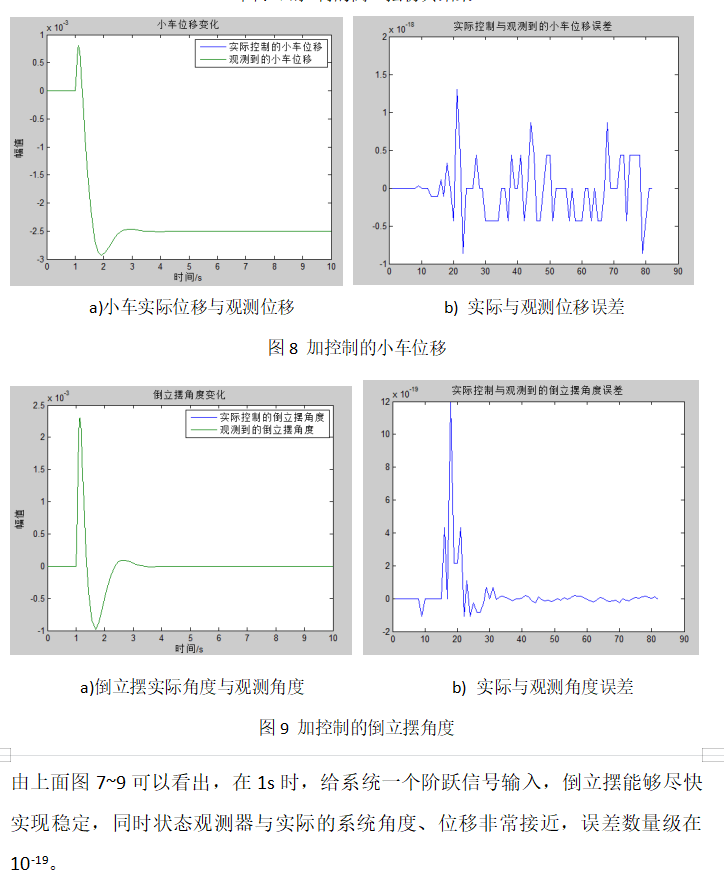
3.5 LRQ控制

线性二次型性能指标易于分析、处理和计算，而且通过线性二次型最优设计方法得到的倒立摆系统具有较好的鲁棒性与动态特性以及能够获得线性反馈结构等优点，因而在实际的倒立摆控制系统设计中得到了广泛的应用。但是在使用该方法时，最优控制的效果取决于加权阵Q和R的选取。

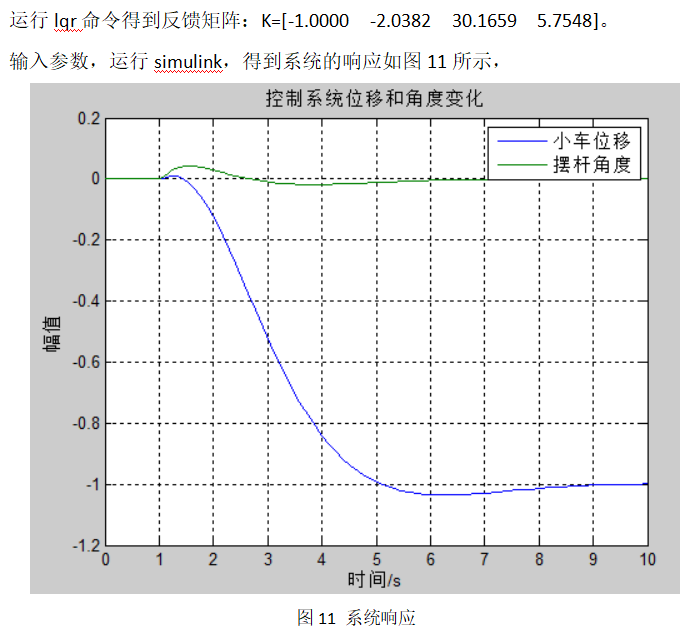
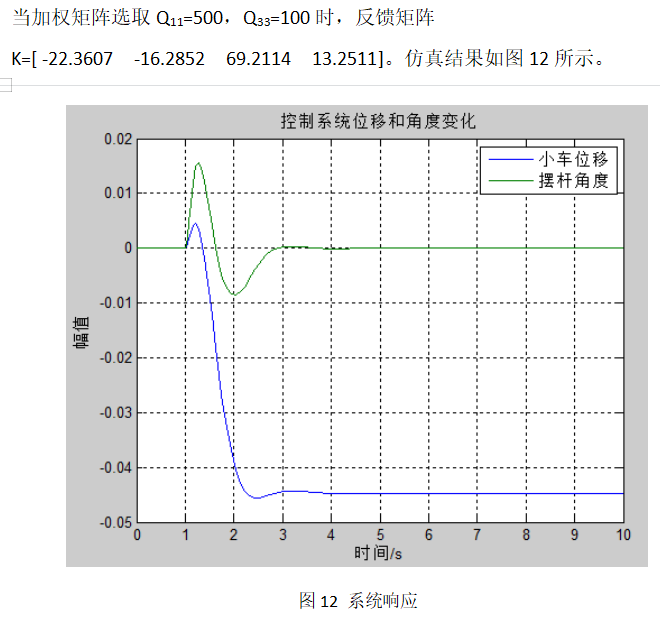
从上述图中可以发现，Q矩阵中，增加Q11、Q33，系统响应时间有明显改善，稳定时间和上升时间变短，并且使摆杆的角度变化减少。增大Q11、Q33，系统的响应还会更快，但是对于实际离散控制系统，过大的控制量会引起系统震荡。反复试验当取Q11=1000，Q33=200时，如图12所示，此时摆杆角度超调足够小，稳态误差满足要求，稳定时间也不超过2秒，达到了良好的控制效果。

附录

MATLAB代码如下：

clear;clc%%A=[0 1 0 0;0 -0.0883 0.6293 0;0 0 0 1;0 -0.2357 27.8285 0];B=[0;0.8832;0;2.3566];C=[1 0 0 0;0 0 1 0];D=[0;0];Q=C'*C;R=1;K=lqr(A,B,Q,R)P=[-24,-24,-2.4+3.2*1i,-2.4-3.2*1i] ;K=acker(A,B,P)P1=[-8.01 -7.99 -8.02 -7.98];%P1=[-48.01 -47.99 -8.02 -7.98];G=(place(A',C',P1))' %% 启动simulink模型sim('model_daolibai.slx')figure(1)plot(tout,yout(:,1),tout,yout(:,2),tout,yout(:,3),tout,yout(:,4))legend('实际控制的小车位移','实际控制的小车角度','观测到的倒立摆位移','观测到的倒立摆角度')title('控制系统位移和角度变化')xlabel('时间/s')ylabel('幅值')figure(2)plot(tout,yout(:,1),tout,yout(:,3))legend('实际控制的小车位移','观测到的小车位移')title('小车位移变化')xlabel('时间/s')ylabel('幅值')figure(3)y=yout(:,1)-yout(:,3);plot(y)title('实际控制与观测到的小车位移误差')figure(4)plot(tout,yout(:,2),tout,yout(:,4))legend('实际控制的倒立摆角度','观测到的倒立摆角度')title('倒立摆角度变化')xlabel('时间/s')ylabel('幅值')figure(5)y=yout(:,2)-yout(:,4);plot(y)title('实际控制与观测到的倒立摆角度误差') %% 00Q=C'*C;K=lqr(A,B,Q,R)sim('untitled10528_1.slx')figure(1)plot(tout,yout(:,1),tout,yout(:,2))legend('小车位移','摆杆角度')grid ontitle('控制系统位移和角度变化')xlabel('时间/s')ylabel('幅值')%% 11Q(1,1)=500;Q(3,3)=100;K=lqr(A,B,Q,R)sim('untitled10528_1.slx')figure(1)plot(tout,yout(:,1),tout,yout(:,2))legend('小车位移','摆杆角度')grid ontitle('控制系统位移和角度变化')xlabel('时间/s')ylabel('幅值')%% 22Q(1,1)=1000;Q(3,3)=200;K=lqr(A,B,Q,R)sim('untitled10528_1.slx')figure(1)plot(tout,yout(:,1),tout,yout(:,2))legend('小车位移','摆杆角度')grid ontitle('控制系统位移和角度变化')xlabel('时间/s')ylabel('幅值') %% 33Q(1,1)=2000;Q(3,3)=1000;K=lqr(A,B,Q,R)sim('untitled10528_1.slx')figure(1)plot(tout,yout(:,1),tout,yout(:,2))legend('小车位移','摆杆角度')grid ontitle('控制系统位移和角度变化')xlabel('时间/s')ylabel('幅值')差')