参考资料：

• PCA
• Whitening
• Implementing PCA/Whitening
• 白化：https://my.oschina.net/findbill/blog/543485
  

什么是白化？

维基百科给出的描述是：

即对数据做白化处理必须满足两个条件：

1. 使数据的不同维度去相关；

2. 使数据每个维度的方差为1；

条件1要求数据的协方差矩阵是个对角阵；条件2要求数据的协方差矩阵是个单位矩阵

为什么使用白化？

教程给出的解释是：

假设训练数据是图像，由于图像中相邻像素之间具有很强的相关性，所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性。

比如在独立成分分析（ICA）中，对数据做白化预处理可以去除各观测信号之间的相关性，从而简化了后续独立分量的提取过程，而且，通常情况下，数据进行白化处理与不对数据进行白化处理相比，算法的收敛性较好。

白化是一种重要的预处理过程，其目的就是降低输入数据的冗余性，使得经过白化处理的输入数据具有如下性质：

• (i) 特征之间相关性较低；
• (ii) 所有特征具有相同的方差。

白化处理分PCA白化和ZCA白化，PCA白化保证数据各维度的方差为1，而ZCA白化保证数据各维度的方差相同。

PCA白化可以用于降维也可以去相关性，而ZCA白化主要用于去相关性，且尽量使白化后的数据接近原始输入数据。

1.PCA白化

根据白化的两个要求，我们首先是降低特征之间的相关性。

在PCA中，我们选取前K大的特征值的特征向量作为投影方向，如果K的大小为数据的维度n，把这K个特征向量组成选择矩阵U（每一列为一个特征向量），为旋转后的数据

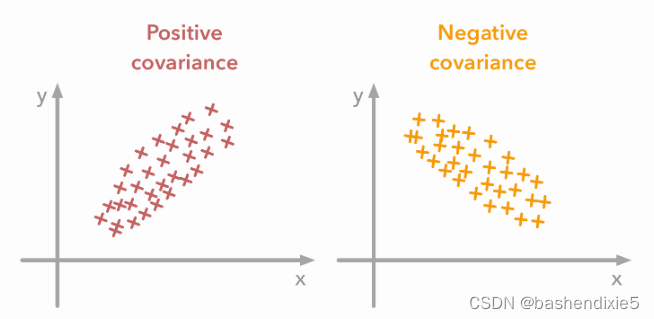
如果K<n，就是PCA降维，如果K=n，则降低特征间相关性降低。

原始数据分布：

PCA旋转后数据分布

上图显示了原始数据和经过PCA旋转之后的数据，可以发现数据之间的相对位置都没有改变，仅仅改变了数据的基，但这种方法就降低了数据之后的相关性。（原始数据的相关性为正，因为x1增加时，x2也增加；而处理之后的数据的相关性明显降低）

第二个要求是每个输入特征具有单位方差，以直接使用作为缩放因子来缩放每个特征，计算公式：

经过PCA白化处理的数据分布如下图所示，此时的协方差矩阵为单位矩阵。

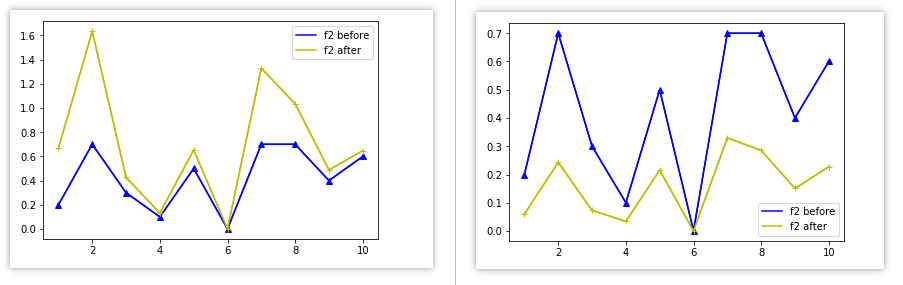
PCA白化与ZCA白化对比
PCA白化

ZCA白化：

2、ZCA白化：

ZCA白化的定义为：

ZCA白化只是在PCA白化的基础上做了一个旋转操作，使得白化之后的数据更加的接近原始数据。

ZCA白化首先通过PCA去除了各个特征之间的相关性，然后是输入特征具有单位方差，此时得到PCA白化后的处理结果，然后再把数据旋转回去，得到ZCA白化的处理结果，感觉这个过程让数据的特征之间有具有的一定的相关性，

下面实验进行验证。

在实验中，我分别计算了原始数据，旋转后数据，PCA白化以及ZCA白化的协方差矩阵，数据用的是UFLDL的实验数据，是个协方差矩阵分别为：

<---仅是分隔作用--->

猜测ZCA白化后的数据的相关性会比PCA白化的要强，在该实验室中表明好像感觉是对的，ZCA白化后主对角线以外的值的绝对值大于PCA白化后（今天看了下发现这个有问题），虽然这种比较可以忽略不计，应该他们的值都是非常的接近的。

3.PCA白化和ZCA白化的区别

PCA白化ZCA白化都降低了特征之间相关性较低，同时使得所有特征具有相同的方差。

• PCA白化需要保证数据各维度的方差为1，ZCA白化只需保证方差相等。
• PCA白化可进行降维也可以去相关性，而ZCA白化主要用于去相关性。

• 4.正则化
  实践中需要实现PCA白化或ZCA白化时，有时一些特征值在数值上接近于0，这样在缩放步骤时我们除以将导致除以一个接近0的值，这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中，我们使用少量的正则化实现这个缩放过程，即在取平方根和倒数之前给特征值加上一个很小的常数

  
  

  当x在区间 [-1,1] 上时, 一般取值为 

  ---

  参数

  ---

  Deep Learning 优化方法总结 By YuFeiGan 更新日期:2015-07-01

  1.Stochastic Gradient Descent (SGD)

  1.1 SGD的参数

  在使用随机梯度下降（SGD）的学习方法时，一般来说有以下几个可供调节的参数:

  • Learning Rate 学习率
  • Weight Decay 权值衰减
  • Momentum 动量

  • Learning Rate Decay 学习率衰减

    ps:
    再此之中只有第一的参数（Learning Rate）是必须的，其余部分都是为了提高自适应性的参数，也就是说后3个参数不需要时可以设为0。

  1.1.1 Learning Rate

  学习率决定了权值更新的速度，设置得太大会使结果越过最优值，太小会使下降速度过慢。
  仅靠人为干预调整参数需要不断修改学习率，因此后面3种参数都是基于自适应的思路提出的解决方案。

  
  

  1.1.2 Weight decay

  在实际运用中，为了避免模型的over-fitting，需要对cost function加入规范项。

  Weight decay adds a penalty term to the error function.

  在SGD中我们加入 −ηλWi 这一项来对cost function进行规范化。

  
  

  这个公式的基本思路是减小不重要的参数对结果的影响，而有用的权重则不会受到Weight decay的影响

• Link 1

  Link 2

  大家都知道DNN常有overfiting的问题，有人会想到为何有些算法（比如DT/最近邻等）在training data上很快达到100%，而NN却需要不停训练却一直达不到。原因之一是相对训练数据中模式，网络参数过多且不加合理区分，导致判决边界调谐到特定训练数据上，并非表现一般特性。由于初始weight is small, neur执行在线性范围，随着training，nonlinear才逐渐显现，decision boundary变弯。但gradient descent完成之前停止training则可避免overfiting。

  其实在dropout被叫响之前，它有个哥们叫weight decay技术，对于非常多weight的NN，along with training，decay all weights。小权值网络更适于做线性判别模型。weight decay具体公式有需要的可以找我。有人会问有价值的weight是不是也会decay。其实BP算法本质能对降低error function意义不大的weight变的越来越小，对于如此小的值，可以完全discard（是不是想起了dropout，呵）。而真正解决问题的weight不会随便被decay。还有些其他本质我们后续再讨论。

  对于activation function的选择是个技巧，但有规律可循。其实很多人忽视了sigmoid的2个参数gamma和phi，直接用“裸体的”sigmoid。想了解“穿着衣服的"sigmoid的可以再联系我。如果有prior information，比如分布有GMD引起的，则gaussian形式的函数将是个好选择(有没有想到ReLU的曲线与sigmoid的曲线分布类似，至于对x<0的y限制为0的本质下回分解吧)。没有这些prior时，有三个基本原则(但不是死的)：非线性，saturability，连续光滑性（这点有待再探讨）。nonlinear是提供deep NN比shallow NN强的计算能力的必要条件。saturability限制weight和activation function的上下边界，因而是epoch可以有限。光滑连续性希望f和一阶导在自变量范围内有意义。

  momentum的概念来自newton第一定律，在BP算法中引入momentum的目的是允许当误差曲面中存在平坦区时，NN可以更快的速度学习。将随机反向传播中的学习规则修正为包含了之前k次权值更新量的alpha倍。具体公式表达有需要的可以找我。（是不是启发你想到了adagrad/adadelta呢，其实看到公式后你更有启发，呵）。momentum的使用"平均化"了随机学习这种weight的随机更新，增加了稳定性，在加快learning中甚至可以远离常引起错误的平坦区。

  误差函数常采用cross entropy，是因为它本质上度量了概率分布间的"距离"。具体公式有需要的可以联系我，一起讨论。此外，如果想得到局部性强的分类器可以考虑闵科夫斯基误差。是的，还有其他物理意义的误差函数，采用哪一种要看用来干什么了。

  对于batch learning，online learning, random learning（据悉msra有更多标注语音但就用了2000小时语音训练）仁者见仁智者见智，这也是为什么jeff dean设计DistBelief提供了Downpour和Sandblaster了。当training data巨大时，内存消耗很大（即使分布式的在内存中存的下但要考虑是否必要），工业界使用的NN常采用online或random协议。在batch learning中样本的重复出现提供的信息同随机情况下样本的单次出现一样多，而实际问题并不需要精确复制各个模式以及实际dataset常有高冗余度，batch learning比random learning慢。但不易嵌入到online learning的"二阶技术"却在某些问题上有其他优势。

  对于DNN来说，BP层层计算很耗时。二阶导数矩阵(Hesse阵)规模可能又很大。大家知道的拟合较好的方法，如LBFGS、共轭梯度法、变量度量法等，保持了较快的收敛速度。但值得一提的是，对Hesse阵的无偏近似方法Curvature Propagation可以参考ilya的论文哦。从此paper中也可理解下BP与Hesse的"秘密"。

  大家都头疼learningRate的选择，其实这个与上述讨论的多个方面有关系，例如NN的结构、activation function形式、momentum策略、decay方式、期望迭代的总次数、优化的方式、期望目标分类器的表现等等。有一点，我们可以利用误差的二阶导数来确定learning rate。也可以利用二阶信息对NN中unnecessary weight的消去做指导。

  1.1.3 Learning Rate Decay

  一种提高SGD寻优能力的方法，具体做法是每次迭代减小学习率的大小。

  
  

  在许多论文中，另一种比较常见的方法是迭代30-50次左右直接对学习率进行操作(η ← 0.5⋅η)

  1.1.4 Momentum

  灵感来自于牛顿第一定律，基本思路是为寻优加入了“惯性”的影响，这样一来，当误差曲面中存在平坦区SGD可以一更快的速度学习。

  
  

  注意：这里的表示方法并没有统一的规定，这里只是其中一种

  Link 1
  Link 2-pdf
  Link 3
  Link 4-pdf

  SGD优缺点
  实现简单，当训练样本足够多时优化速度非常快
  需要人为调整很多参数，比如学习率，收敛准则等
  Averaged Stochastic Gradient Descent (ASGD)
  在SGD的基础上计算了权值的平均值。
  $$\bar{w}t=\frac{1}{t-t_0}\sum^t{i=t_0+1} w_t$$

  ASGD的参数
  在SGD的基础上增加参数t0t0
  学习率 ηη
  参数 t0t0
  ASGD优缺点
  运算花费和second order stochastic gradient descent (2SGD)一样小。
  比SGD的训练速度更为缓慢。
  t0t0的设置十分困难
  Link 1

  1. Conjugate Gradient（共轭梯度法）
     介于最速下降法与牛顿法之间的一个方法，它仅仅需要利用一阶导数的信息，克服了GD方法收敛慢的特点。

  Link 1

  Limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) (一种拟牛顿算法)
  L-BFGS算法比较适合在大规模的数值计算中，具备牛顿法收敛速度快的特点，但不需要牛顿法那样存储Hesse矩阵，因此节省了大量的空间以及计算资源。

  Link 1
  Link 2
  Link 3

  应用分析
  不同的优化算法有不同的优缺点，适合不同的场合:

  LBFGS算法在参数的维度比较低（一般指小于10000维）时的效果要比SGD（随机梯度下降）和CG（共轭梯度下降）效果好，特别是带有convolution的模型。
  针对高维的参数问题，CG的效果要比另2种好。也就是说一般情况下，SGD的效果要差一些，这种情况在使用GPU加速时情况一样，即在GPU上使用LBFGS和CG时，优化速度明显加快，而SGD算法优化速度提高很小。
  在单核处理器上，LBFGS的优势主要是利用参数之间的2阶近视特性来加速优化，而CG则得得益于参数之间的共轭信息，需要计算器Hessian矩阵。