博主是初学近世代数（群环域），本意是想整理一些较难理解的定理、算法，加深记忆也方便日后查找；如果有错，欢迎指正。
我整理成一个系列：近世代数，方便检索。

有一些概念。

• 置换permutation：设集合$S$是一个有限非空集合，$G$是$S$到它自身上的所有元素一一映射，即$\pi :S\to S$。
  

• 对称群symmetric group：当$S$为具有$n$个元素的有限集合 时，它的全部置换（所有一一映射，每个一一映射是所有元素的一一映射）所组成的群$G$也称为$n$次对称群，记为$S_n$。

例子： S = { 1 , 2 , 3 } S=\{1,2,3\} S={1,2,3}
$S_n=$ { { 1 , 2 , 3 } { 1 , 2 , 3 } } , { { 1 , 2 , 3 } { 1 , 3 , 2 } } , { { 1 , 2 , 3 } { 2 , 1 , 3 } } , { { 1 , 2 , 3 } { 2 , 3 , 1 } } , { { 1 , 2 , 3 } { 3 , 1 , 2 } } , { { 1 , 2 , 3 } { 3 , 2 , 1 } } \left\{ \begin{aligned} \{1,2,3\}\\ \{1,2,3\} \end{aligned} \right\}, \left\{ \begin{aligned} \{1,2,3\}\\ \{1,3,2\} \end{aligned} \right\}, \left\{ \begin{aligned} \{1,2,3\}\\ \{2,1,3\} \end{aligned} \right\}, \left\{ \begin{aligned} \{1,2,3\}\\ \{2,3,1\} \end{aligned} \right\}, \left\{ \begin{aligned} \{1,2,3\}\\ \{3,1,2\} \end{aligned} \right\}, \left\{ \begin{aligned} \{1,2,3\}\\ \{3,2,1\} \end{aligned} \right\} {{1,2,3}{1,2,3}​},{{1,2,3}{1,3,2}​},{{1,2,3}{2,1,3}​},{{1,2,3}{2,3,1}​},{{1,2,3}{3,1,2}​},{{1,2,3}{3,2,1}​}

简写： S n = { ( 1 ) , ( 2 , 3 ) , ( 1 , 2 ) , ( 1 , 2 , 3 ) , ( 1 , 3 , 2 ) , ( 1 , 3 ) } S_n=\{(1),(2,3),(1,2),(1,2,3),(1,3,2),(1,3)\} Sn​={(1),(2,3),(1,2),(1,2,3),(1,3,2),(1,3)}

• 置换群permutation group：置换群是对称群的子群。
• 轮换cycle：$S$是有限非空集合，如果我们从$S$中任意元素$x$开始重复置换，得到$\pi (x),\pi (\pi (x)),\dots \dots$直到某个置换返回$x$，那么我们称这些置换为一个轮换。
  
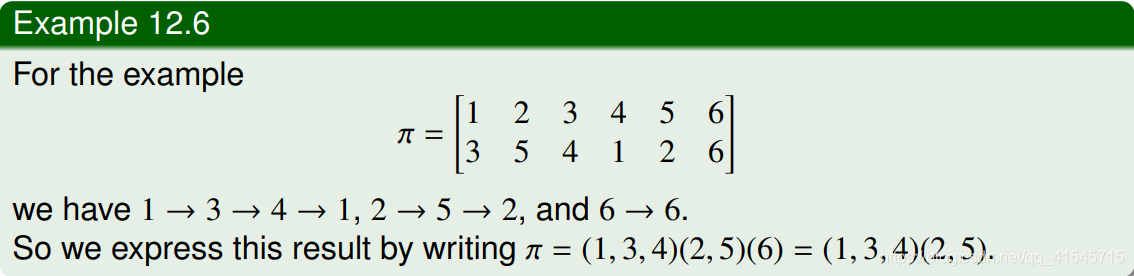
• 对换transposition：只有两个元素的轮换。
• 不相交的轮换disjoint cycle：两个轮换 σ = { i 1 , i 2 … … i r } ， τ = { j 1 , j 2 … … j s } ， \sigma=\{i_1,i_2……i_r\}，\tau=\{j_1,j_2……j_s\}， σ={i1​,i2​……ir​}，τ={j1​,j2​……js​}，如果有$i_k\ne j_l,k=1,2,\dots \dots r,l=1,2\dots \dots s$，那么我们称这两个轮换$\sigma ,\tau$不相交。两个不相交轮换的乘积是可交换的commutative：$\sigma \cdot \tau =\tau \cdot \sigma$。

例子：$(1,3,4)，(2,5)$。可交换的：$(1,3,4)\cdot (2,5)=(2,5)\cdot (1,3,4)$

置换的分解

任何置换都可以分解成不相交的轮换的乘积，而且分解成的轮换是唯一的。

证明：数学归纳法
假设集合$|S|=n$，

• 当$n=1$，则$\tau =(1)$；
• 假设$n-1$时结论成立；即${\alpha }^{n-1}$可以写成${\alpha }_1\cdot {\alpha }_2\dots \dots \cdot {\alpha }_r$的形式，其中${\alpha }_i,(i=1\dots \dots r)$是一个轮换，${\alpha }_i、{\alpha }_j(i\ne j)$不相交
• 现在证明 S = { 1 , 2 , 3 … … , n } S=\{1,2,3……,n\} S={1,2,3……,n}
  取一个置换：${\alpha }^n=$$$\left\{\begin{array}{r}1\\ i_1\end{array}\right\},\left\{\begin{array}{r}2\\ i_2\end{array}\right\},\dots \dots ,\left\{\begin{array}{r}n-1\\ i_{n-1}\end{array}\right\},\left\{\begin{array}{r}n\\ i_n\end{array}\right\}$$
  有两种情况：
  • $i_n=n$，这种情况直接得出${\alpha }^n={\alpha }^{n-1}\cdot (n)={\alpha }_1\cdot {\alpha }_2\dots \dots \cdot {\alpha }_r\cdot (n)$，是不相交的轮换的乘积形式；
  • $i_n\ne n$，则有 ∃ k ∈ { 1 , 2 … … n − 1 } ， i k = n ， α n = {\exists} k\in \{1,2……n-1\}，i_k=n，\alpha^{n}= ∃k∈{1,2……n−1}，ik​=n，αn=$$\left\{\begin{array}{r}1\\ i_1\end{array}\right\},\left\{\begin{array}{r}2\\ i_2\end{array}\right\},\dots \dots ,\left\{\begin{array}{r}k-1\\ i_{k-1}\end{array}\right\},\left\{\begin{array}{r}k\\ i_k\end{array}\right\},\left\{\begin{array}{r}k+1\\ i_{k+1}\end{array}\right\},\dots \dots \left\{\begin{array}{r}n-1\\ i_{n-1}\end{array}\right\},\left\{\begin{array}{r}n\\ i_n\end{array}\right\}$$
    • 这样 i k = n ， i n ∈ { 1 , 2 … … n − 1 } ， i_k=n，i_n\in \{1,2……n-1\}， ik​=n，in​∈{1,2……n−1}，有${\alpha }^n=(i_k,i_n){\alpha }^{n-1}\cdot (n)$，即**先把$i_n$换到前$n-1$个对应关系中，然后就跟前一种可能是一样的。**展开来，${\alpha }^n=(i_k,i_n)\cdot {\alpha }_1\cdot {\alpha }_2\dots \dots \cdot {\alpha }_r$。
    • 在${\alpha }_1,{\alpha }_2\dots \dots ,{\alpha }_r$中必定存在一个，且只存在一个（因为${\alpha }_i,(i=1\dots \dots r)$彼此不相交）${\alpha }_i$包含$i_n$，即$a_i$与$(i_k,i_n)$相交。
    • 假设是${\alpha }_1$,可以写成${\alpha }_1=(i_n,a,\dots \dots b)$，那么$(i_k,i_n)\cdot {\alpha }_1=(i_k,i_n,a,\dots \dots b),{\alpha }^n=(i_k,i_n)\cdot {\alpha }_1\cdot {\alpha }_2\dots \dots \cdot {\alpha }_r=(i_k,i_n,a,\dots \dots b)\cdot {\alpha }_2\dots \dots \cdot {\alpha }_r$，是互不相交的轮换，证毕。

置换的级计算

置换$\sigma$：

• 本身是$r$长轮换的话，那$ord(\sigma )=r$
• 如果不是轮换，则置换可以分解为轮换，$\sigma ={\sigma }_1\cdot {\sigma }_2\cdot \dots \dots \cdot {\sigma }_t$，其中${\sigma }_i$为轮换；那么$ord(\sigma )=l.c.m(ord({\sigma }_1),ord({\sigma }_2),\dots \dots ord({\sigma }_t))$,$l.c.m()$是求最小公倍数。

理解，为什么置换的级是分解轮换级的最小公倍数：

• 轮换的级：$ord({\sigma }_i)$的意思是最少“转多少次”才能使数字不变；例子：$(1,3,4)=$$$\left\{\begin{array}{r}1\\ 3\end{array}\right\},\left\{\begin{array}{r}3\\ 4\end{array}\right\},\left\{\begin{array}{r}4\\ 1\end{array}\right\}$$
  “转1次”：$(3,4,1)$
  “转2次”：$(4,1,3)$
  “转3次”：$(1,3,4)$
  所以$ord((1,3,4))=3$
  任意轮换的级就是这个轮换的元素个数
• 置换的级：置换分解成了多个轮换，那么我们需要将这个置换转每个轮换级的最小公倍数次，才能使所有元素都不变。例子：$(1,3,4,2,5)=(1,3,4)(2,5),(1,3,4)$需要转3次，$(2,5)$需要转2次，那么$(1,3,4,2,5)$需要转6次。