实验要求
1)设计模拟实现OPT、FIFO和LRU页面置换算法中的任意一种。
OPT算法:需要发生页面置换时,算法总是选择在将来最不可能访问的页面进行置换。
FIFO算法:算法总是选择在队列中等待时间最长的页面进行置换。
LRU算法:如果某一个页面被访问了,它很可能还要被访问;相反,如果它长时间不被访问,那么,在最近未来是不大可能被访问的。
2)完成算法代码。
3)运行程序,算出结果。
设计思路
模拟一个拥有若干个虚页的进程在给定的若干个实页中运行、并在缺页中断发生时使用OPT算法进行页面置换的情形。其中内存页面大小可手动输入进行设置,虚页的个数可以事先给定(例如10个),对这些虚页访问的页地址流(其长度可以事先给定,例如20次虚页访问)可以由程序随机产生,也可以手动输入。要求程序运行时屏幕能显示出置换过程中的状态信息并输出访问结束时的页面命中率。
实验结果与分析:
最佳置换算法:一个进程在内存的若干个页面中,哪一个页面是未来最长时间内不再被访问的,那么如果发生缺页中断时,就将该页面换出,以便存放后面调入内存中的页面。
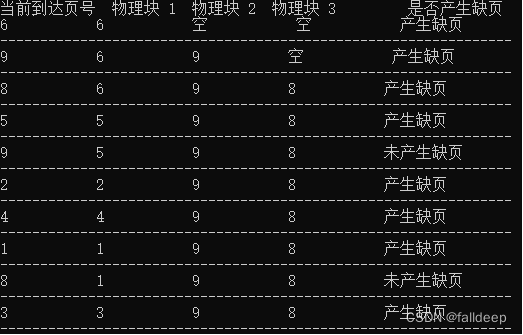
程序进入时可通过程序设定物理块大小
接着输入虚页长度,即程序运行时页面号引用串长度
程序有两种页地址流产生方式,分别为系统随机产生和手动输入
最后输出总的命中次数和命中率

![]()
源程序
#include<iostream>
#include<cstring>using namespace std;const int N = 1e3 + 10;
int h[N], data[N], temp[N];//分配的物理块 虚页流 存储该页面未来要被访问的时间
int n, m;//物理块大小 虚页的长度
double sum;//总命中次数 void init()
{cout << "最佳置换算法OPT 请输入物理块大小" << endl;cin >> n;cout << "请输入虚页长度" << endl;cin >> m; cout << "请选择页地址流产生方式\n1.系统随机生成,2.手动输入" << endl;int op;cin >> op;if(op == 1)//随机生成 {for(int i = 1; i <= m; i ++) {data[i] = ( rand() % (9 - 1 + 1 ) ) + 1;//产生[1,9]的随机数 cout << data[i] << ' '; }cout << endl;} else if(op == 2)//手动输入 {for(int i = 1; i <= m; i ++) cin >> data[i];}cout << "当前到达页号 ";for(int i = 1; i <= n; i ++)cout << "物理块 " << i << " ";cout << " 是否产生缺页" << endl;
} void show(int k, bool flag)//当前虚页块位号 是否产生缺页
{cout << data[k] << " ";for(int i = 1; i <= n; i ++){if(h[i] == 0) cout << "空 ";else cout << h[i] << " "; } if(flag) cout << "未产生缺页";else cout << "产生缺页"; cout << "\n----------------------------------------------------------------" << endl;
}int main()
{init();//初始化for(int i = 1; i <= m; i ++)//对虚页流进行处理 {bool flag = false;//当前内存中是否有该页面 int j = data[i];//该页面下标for(int k = 1; k <= n; k ++)//遍历物理块if(h[k] == j)//当前内存中有该页面 {flag = true;//cout << "here" << endl;sum ++;//命中次数加1 break; } bool temp_flag = flag;//保存标志位if(!flag)//当前内存中无该页面,需调用页面置换算法(先检查有无空白物理块){for(int k = 1; k <= n; k ++)if(h[k] == 0)//当前有空白物理块,将该页面置于此处 {h[k] = j;//cout << "here" << endl;flag = true;//此时flag代表该页面放入内存没 break;}}if(!flag)//无空白物理块, 采用OPT算法 {memset(temp, 0x3f, sizeof temp);//temp用来存放下一次被访问的位置,默认为0x3f代表未来不被访问for(int q = 1; q <= n; q ++)//遍历物理块 for(int k = i + 1; k <= m; k ++)//遍历后续页面流if(data[k] == j)//找到下一次被访问的位置 {temp[q] = k; break; } int max = temp[1], t = 1;//最大访问位置,及其下标 for(int k = 2; k <= n; k ++)//遍历物理块,找到最晚被访问的页面if(temp[k] > max){t = k;max = temp[k];} h[t] = j;//将该页面置换进入 }show(i, temp_flag);//打印输出数据 }cout << "命中次数为 " << sum << " 虚页流长度 " << m << " 命中率为 " << sum / m;return 0;
}