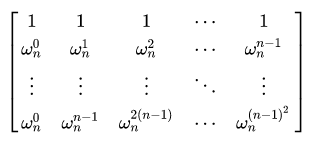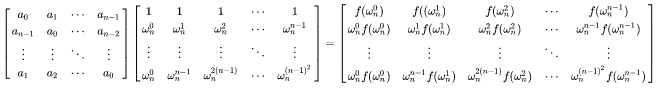置换矩阵

题解

首先对于有大于1个环的情况，明显行列式值是为零的。
因为这种情况必定有一个环的长度小于$\left|\frac{n}{2}\right|$，所以就一定可以将一个环的区域全部消成0，这样答案就肯定为0了。

那么对于$p_1=n,p_i=i-1$的部分呢，我可以很容易看出这是一个循环行列式。
对于循环行列式的值，我们有着一种特别的求法。
$$det(A)=\prod _{i=0}^{i-1}(\sum _{j=0}^{n-1}{a}_j{\omega }^{ij})$$
令$f(x)={\sum }_{j=0}^{n-1}{a}_j{x}^j$，那么有
$$det(A)=\prod _{i=0}^{i-1}f({\omega }^i)$$
其中$\omega$表示单位根

证明：
考虑范蒙德矩阵，

其中${\omega }_n$表示$n$次单位根，即${\omega }_n=e^{\frac{2\pi }{n}}$
将范德蒙矩阵与$n$阶循环行列式相乘，由于${\omega }_n^{n+k}={\omega }_n^k$，有

两边取行列式，则有
$$det(A)det(V)=(\prod _{i=0}^{n-1}f({\omega }_n^j))det(V)$$
考虑到$det(V)={\prod }_{0⩽j<i<n}({\omega }_n^i-{\omega }_n^j)$
且$w_n^0,w_n^1,...w_n^{n-1}$互不相等，故$det(V)\ne 0$，有
$$det(A)=\prod _{i=0}^{i-1}f({\omega }^i)$$
证毕

但我们在模的意义下有如何计算呢？
考虑到${\omega }^0,{\omega }^1,...,{\omega }^{n-1}$是$B(x)=x^n-1$的所有根，我们可以通过这东西来进行计算。
设${\lambda }_1,{\lambda }_n$是$n$次多项式$A(x)=f(x)$的所有根，${\mu }_1,...,{\mu }_m$是$m$次多项式$B(x)$的所有根，
定义函数$F(A，B)=b_m^n{\prod }_{i=1}^{m}A({\mu }_i)$，显然$F(A,B)$就是我们要求的答案
显然有
$$F(A,B)=b_m^n\prod _{i=1}^{n}A({\mu }_i)=a_n^m{b}_m^n\prod ({\mu }_i-{\lambda }_j)=(-1{)}^{nm}{a}_n^m\prod _{i=1}^{n}B({\lambda }_i)$$
结合定义，可以得到以下性质

• $F(A,B)=(-1{)}^{nm}F(B,A)$
• $F(A,B)=a_n^m{b}_m^n(n=0\vee m=0)$
• $F(A-CB,B)=F(A,B)(b_m=1)$
• $F(A,B)=(-1{)}^{deg(A)-deg(A-CB)}F(A-CB,B)$

于是此时我们就可以$O(n^2)$地计算出这样行列式的值了。

但对于不是循环行列式的行列式呢？
我们发现我们对于原循环求出的行列式可以通过对某些列的交换达到来改变原序列，从而使它成为循环行列式。
我们接着就可以发现交换次数只会改变的行列式的正负，而交换次数又是等于点一的路径的序列的逆序对数的。
所以我们只需要做完子任务3后求一下逆序对数，将答案改变一下正负就能够完成subtask4了。

总时间复杂度还是$O\left(n^2\right)$。

源码

一个正负判断了一个下午。。。

#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
#include<set>
#include<map>
using namespace std;
#define MAXN 5005
#define lowbit(x) (x&-x)
#define reg register
typedef long long LL;
typedef unsigned long long uLL;
typedef unsigned int uint;
typedef pair<int,int> pii;
const int INF=0x7f7f7f7f;
const int mo=1e9+7;
const double PI=acos(-1.0);
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){_T f=1;x=0;char s=getchar();while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}x*=f;
}
int n,m,a[MAXN],p[MAXN],q[MAXN],A[MAXN],B[MAXN],pp[MAXN];
int add(int x,int y){return x+y<mo?x+y:x+y-mo;}
int qkpow(int a,int s){int t=1;while(s){if(s&1)t=1ll*a*t%mo;a=1ll*a*a%mo;s>>=1;}return t;}
signed main(){freopen("matrix.in","r",stdin);freopen("matrix.out","w",stdout);read(n);m=n;int ans=1,now=1,tmp=0,sum=0;for(int i=1;i<=n;i++)read(a[i]);for(int i=1;i<=n;i++)read(p[i]),q[p[i]]=i;pp[1]=1;now=q[1];tmp++;while(now^1)pp[tmp+1]=now,now=q[now],tmp++;if(tmp<n){puts("0");return 0;}for(int i=1;i<=n;i++)for(int j=i+1;j<=n;j++)if(pp[i]>pp[j])sum++;for(int i=0;i<n;i++)A[i]=a[pp[i+1]];B[0]=mo-1;B[m]=1;n--;ans=1;while(1){if(n<m)swap(A,B),ans=(n&m)&1?mo-ans:ans,swap(n,m);if(!m){ans=1ll*ans*qkpow(B[0],n)%mo;break;}const int d=1ll*A[n]*qkpow(B[m],mo-2)%mo;for(int i=m;i>=0;i--)A[n-m+i]=add(A[n-m+i],mo-1ll*d*B[i]%mo);int L=0;while(n&&!A[n])n--,L++;ans=1ll*ans*qkpow(B[m],L)%mo;}printf("%d\n",(sum&1)?add(mo,-ans):ans);return 0;
}

谢谢！！！