前言
本篇是最近在学习云台以及姿态融合时,想学习一下卡尔曼滤波的原理,基于 DR_CAN 老师的卡尔曼滤波的视频做的笔记,基本上是按照 DR_CAN 老师的思路自己推导计算了一遍,推荐还是看一下原视频,讲解得很不错:https://space.bilibili.com/230105574/channel/collectiondetail?sid=6939
由递归算法延伸出卡尔曼滤波的思想
对同一个物体进行测量,每次得到的测量数据不尽相同,单次测量的结果记作 z(k),如果要得到较好的实际值的估计值,一般的做法是取平均:

由上面的变换可以提炼出:
k 时刻的估计值 x_hat(k) = 上时刻的估计值 x_hat(k-1) + 系数 * (k 时刻的测量值 - 上时刻的估计值)
当测量次数 k 足够大时,x_hat(k) = x_hat(k-1) ,也就是说,估计值已经确定而不再变化,将其中的 1/k 提炼出来,记作 K(k),则上式转化为:
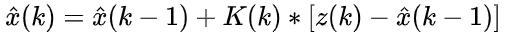
当前估计值 = 上次估计值 + 系数 * (当前测量值 - 上次估计值)
此递归的思想就可以延伸到卡尔曼滤波的思想,是相通的,此系数就可以类比卡尔曼增益。
在卡尔曼滤波中,其增益可简化为:

1)当估计误差远大于测量误差时,k>>1,此时 x_hat(k) = x_hat(k-1) + z(k) - x_hat(k-1) = z(k),此时就完全信任测量值
2)当测量误差远大于估计误差时,k>>0,此时 x_hat(k) = x_hat(k-1),就完全信任估计值
求卡尔曼增益
对离散状态空间引入噪声:

其中 w 表示过程噪声,v 表示测量噪声,两者都假定满足正态分布:
w ~ P(0,Q) v~P(0,R)
Q 与 R 矩阵分别时过程噪声 w 与测量噪声 v 的协方差矩阵
协方差矩阵的公式为:

在概率论中由两个基础公式比较重要,在后面的解算中会经常用到:
1)x 的方差 = x^2 的期望 + x 期望的平方
2)x与y的协方差 = x*y 的期望 + x的期望*y的期望

结合上面的两个公式,对 w,v 来说,期望值都为0 ,也就是 E(w) = 0,E(v) = 0,则
w 的方差 Var(w) = E(w^2) ( E(w) = 0 )
v 的方差 Var(v) = E(v^2) ( E(v) = 0 )
协方差矩阵的含义
例如一个二阶系统,过程噪声 w 的协方差矩阵就为:

结合上式,协方差矩阵的含义就可以理解为:
1)既可以使用主对角线的方差元素表示各状态数据的变化剧烈程度
2)又可以使用协方差元素来表示各状态数据之间的变化关系
先验估计与后验估计
对于上述的状态方程,由于过程噪声未知,将其去掉,写成一般形式的状态方程,通过 A 与 B矩阵计算得到的估计值,称作先验估计,在书写时添加负号来区分:

先验估计值也可以称作通过模型计算得到的估计值。
测量结果是可以直接获取的,通过测量结果 z(k) 可以反推测量状态 x_hat_MEA(k)

由于先验估计值与测量值都是不包含实际误差的,因此都是不可靠的。
卡尔曼滤波器的作用就是从不可靠的先验估计值与不可靠的测量值中得到可靠的估计值,最终得到的估计值就称作后验估计值
结合递归算法的思想,卡尔曼滤波的思想就可以表示为:
后验估计值 = 先验估计值 + 系数 * (测量值 - 先验估计值)

此时系数 G∈[0,1] ,在卡尔曼滤波中,通常将 z(k) 前面的系数消掉,因此将增益设置为:
G = K(k) * H
原式就变为:

如果要求解 K(k) 就需要借助误差与协方差矩阵来求解。
估计误差与协方差矩阵
引入估计误差的概念:

其中 e(k) 表示估计误差,x(k) 表示真实值,x_hat(k) 表示后验估计值
估计误差 e 满足正态分布 p(e)~(0,P),期望值为0,估计误差的协方差矩阵为 P = E[e e']
思路:如果能使协方差矩阵 P 中的主对角线元素,即方差元素值最小,则整体的估计误差 e 的变化就小。
将误差公式代入其协方差矩阵 P,得:

在将卡尔曼滤波的核心公式代入,得到估计误差的表达式:

将 x(k) - x_hat-(k) 记作先验误差 e-(k) ,使用先验误差来表示估计误差,得到:

代入求解估计误差的协方差矩阵:


在求解时,会遇到先验误差的协方差矩阵 P-(k),这个矩阵非常重要。
最终求解出的公式:

就是卡尔曼滤波推导的关键公式,在后续两个部分的求解都依赖此公式:
1)卡尔曼增益K(k)的表达式求解
2)估计误差协方差矩阵P(k) 的更新计算
卡尔曼增益的求解
求解卡尔曼增益需要引入“迹”的概念,矩阵的迹表示矩阵主对角线上的元素之和,记作 tr(A)。矩阵转置后,矩阵的迹是保持不变的。
我们得到了估计误差的协方差矩阵 P(k) 关于卡尔曼增益 K(k) 的表达式(上个步骤的求解结果),前面已经介绍:
协方差矩阵的主对角线元素就是各元素的方差,其他元素是协方差,而卡尔曼滤波的目标是求得最优的估计值,使得估计值更接近真实值,更接近真实值也就是估计误差的方差最小,如果要让估计误差的方差最小,则只需要协方差矩阵的迹最小即可。
关于迹的求解,有两个重要的结论在求解时会用到,可以简化计算:

将上面 P(k) 的表达式进行两边求迹:

之后令估计误差的协方差矩阵 P(k) 的迹对卡尔曼增益 K(k) 求导,求出其导数为0的点,就是估计误差方差最小的卡尔曼增益:

最终,根据对迹的求导,求极值,就可以得到卡尔曼增益的表达式。
求先验误差的协方差矩阵
在上一小节中求解出了卡尔曼增益的表达式,但在表达式中的先验误差的协方差矩阵 P-(k) 的未知的,因此接下来就需要求解先验误差的协方差矩阵 P-(k)。
可以根据其矩阵定义,代入先验估计值的表达式,一直求解就可以得到最终的关系式:

卡尔曼滤波的五大公式
经过上面的计算之后,数据都是已知的了,之后就可以归纳出卡尔曼滤波的五大公式,包含预测与校正两方面:

更新估计误差协方差公式的来历
关于最后一个更新误差协方差的公式,在前面求解卡尔曼增益的原始等式中,包含估计误差协方差与先验误差协方差的关系:

之后利用此等式,求解出了极值时的卡尔曼增益 K(k) 的表达式,之后再将此 K(k) 的表达式回代进去,就可以得到估计误差协方差的式子了:


![凌恩生物文献分享|南农大胡锋教授团队揭示苯并[a]芘胁迫影响蚯蚓肠道病毒组生态适应策略机制](https://img-blog.csdnimg.cn/img_convert/70c2d6e54aa5a29be5462ce0fee18d11.png)



