文章目录
- 1 引言
- 算法
- 数据结构
- 算法和数据结构的关系
- 2 复杂度分析
- 时间复杂度
- 空间复杂度
- 3 数据结构
- 数据与内存
- 数据结构分类
- 4 数组与链表
参考资料
1 引言
算法
算法是一组用于解决特定问题或执行特定任务的明确定义的计算步骤或指令集合。算法可以被视为一种解决问题的方法或策略,它描述了如何将输入转换为输出,通过一系列的逻辑和数学操作来实现预期的结果。
算法可以用来解决各种不同的问题,例如排序数据、搜索元素、图形处理、数据压缩、机器学习等。它们是计算机科学和计算机编程的核心概念。
良好的算法通常具有以下特点:
- 正确性:算法应该能够产生正确的输出,解决给定的问题。
- 效率:算法应该能够在合理的时间内完成任务,避免不必要的计算和资源消耗。
- 可读性:算法应该易于理解和阅读,便于他人理解和维护。
- 可扩展性:算法应该能够处理不同规模和复杂度的问题,并且在输入规模增加时仍保持良好的性能。
算法的设计和分析是计算机科学的重要研究领域,有许多经典的算法被广泛应用于各种领域。常见的算法设计方法包括贪婪算法、分治算法、动态规划、回溯法、图算法等。算法的复杂性分析涉及时间复杂度、空间复杂度、最坏情况复杂度等概念,用于评估算法的效率和可行性。
总之,算法是计算机科学中非常重要的概念,它们是解决问题和执行任务的基础工具,对于计算机程序的设计和优化起着关键作用。
数据结构
数据结构是一种组织和存储数据的方式,旨在使数据的访问和操作更加高效。它定义了一种数据元素之间的关系,并提供了对这些元素进行插入、删除、查找和修改的操作。
常见的数据结构包括:
- 数组(Array):将相同类型的数据元素按照一定的顺序存储在连续的内存空间中。
- 链表(Linked List):通过指针将不同类型的数据元素连接起来,每个元素包含一个指向下一个元素的引用。
- 栈(Stack):一种先进后出(LIFO)的数据结构,只允许在栈顶进行插入和删除操作。
- 队列(Queue):一种先进先出(FIFO)的数据结构,允许在队尾进行插入操作,在队头进行删除操作。
- 树(Tree):一种由节点组成的层次结构,每个节点可以有多个子节点。
- 图(Graph):由节点和节点之间的边组成的数据结构,用于表示各种实体之间的关系。
- 堆(Heap):一种特殊的树结构,具有最大堆和最小堆两种形式,用于高效地获取最大或最小元素。
- 散列表(Hash Table):根据关键字直接访问数据的数据结构,通过哈希函数将关键字映射到存储位置。
数据结构的选择取决于问题的性质和需求。不同的数据结构在空间占用、时间复杂度和操作效率等方面有所不同,合理选择和使用数据结构可以提高程序的性能和效率。
数据结构和算法是计算机科学的核心内容,它们相互依赖,共同构建了计算机程序的基础。理解和掌握不同的数据结构对于解决复杂的计算问题和设计高效的程序非常重要。
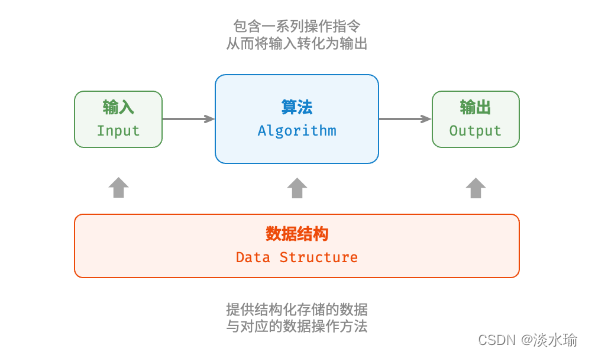
算法和数据结构的关系
算法依赖于数据结构来实现具体的操作和计算,而数据结构提供了算法所需的存储和组织数据的方式。良好的数据结构选择和设计可以提供更好的算法效率和性能。
因此,算法和数据结构是相辅相成的,它们共同构建了计算机科学中的基础。深入理解和掌握数据结构和算法对于设计和开发高效的计算机程序至关重要。
2 复杂度分析
算法效率评估,方法:
时间效率:算法运行速度的快慢。
空间效率:算法占用内存空间的大小。
我们的目标是设计“既快又省”的数据结构与算法。
时间复杂度
时间复杂度是一种衡量算法运行时间随输入规模增长的增长率。它表示算法执行所需的时间与输入规模之间的关系。常见的时间复杂度表示方法包括大O表示法,用于描述最坏情况下的运行时间。
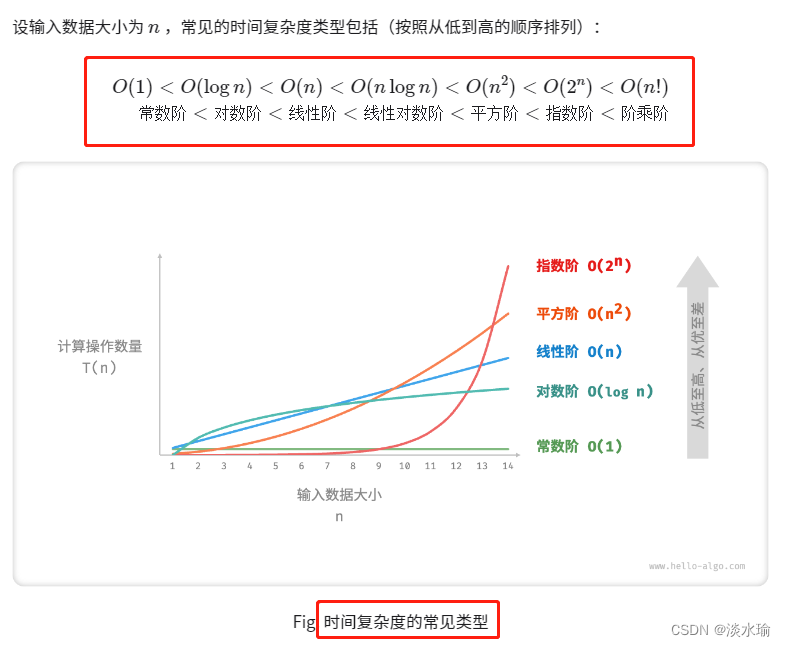
「平均时间复杂度」可以体现算法在随机输入数据下的运行效率。
在进行时间复杂度分析时,我们通常关注最坏情况下的时间复杂度,因为它提供了算法在最不利情况下的性能保证。同时,还可以考虑平均情况下的时间复杂度和最好情况下的时间复杂度。
空间复杂度
空间复杂度是一种衡量算法所需的额外空间随输入规模增长的增长率。它表示算法执行所需的额外空间与输入规模之间的关系。与时间复杂度类似,常见的空间复杂度表示方法也使用大O表示法。
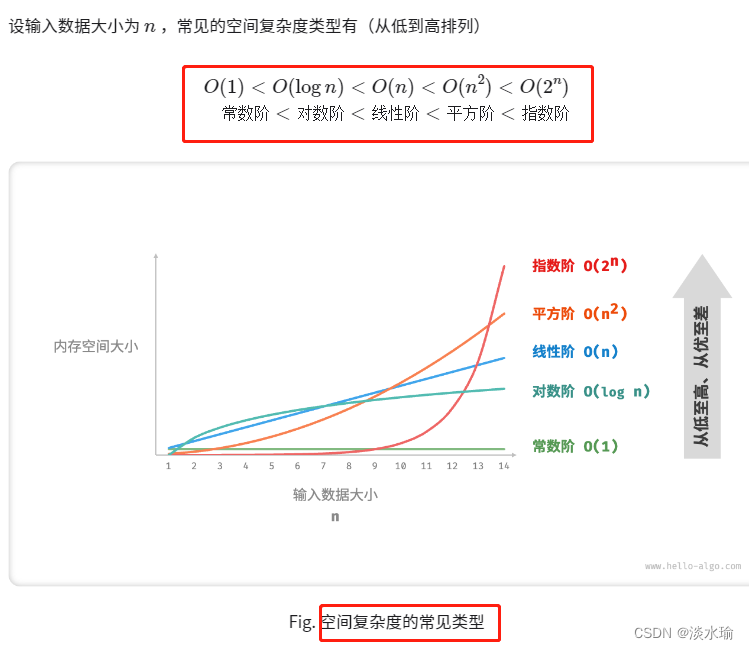
降低时间复杂度通常需要以提升空间复杂度为代价,反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”;反之,则称为“以时间换空间”。
选择哪种思路取决于我们更看重哪个方面。在大多数情况下,时间比空间更宝贵,因此以空间换时间通常是更常用的策略。当然,在数据量很大的情况下,控制空间复杂度也是非常重要的。
3 数据结构
数据与内存
基本数据类型:
数据是指以某种形式或格式表示的信息。在计算机科学和数据结构领域,数据通常是由位(0和1)组成的二进制序列。数据可以包括数字、文字、图像、音频、视频等各种形式的信息。
在计算机科学中,数据可以被组织成不同的数据结构,如数组、链表、栈、队列、树、图等。不同的数据结构适用于不同的场景和问题,可以提供高效的数据存储和访问方式。
「基本数据类型」是 CPU 可以直接进行运算的类型,在算法中直接被使用。
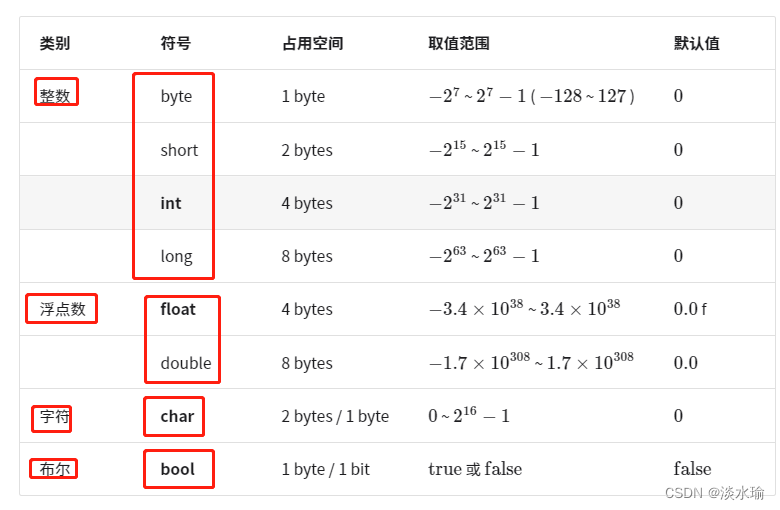
浮点数可以进行各种数学运算,包括加法、减法、乘法、除法等。然而,由于浮点数的内部表示是有限的,存在舍入误差和精度损失的问题。在比较浮点数时,应使用适当的容差值而不是直接进行相等性比较。
计算机内存:
在算法运行过程中,相关数据都存储在内存中。
在数据结构与算法的设计中,内存资源是一个重要的考虑因素。



