PAT甲级 1010 Radix
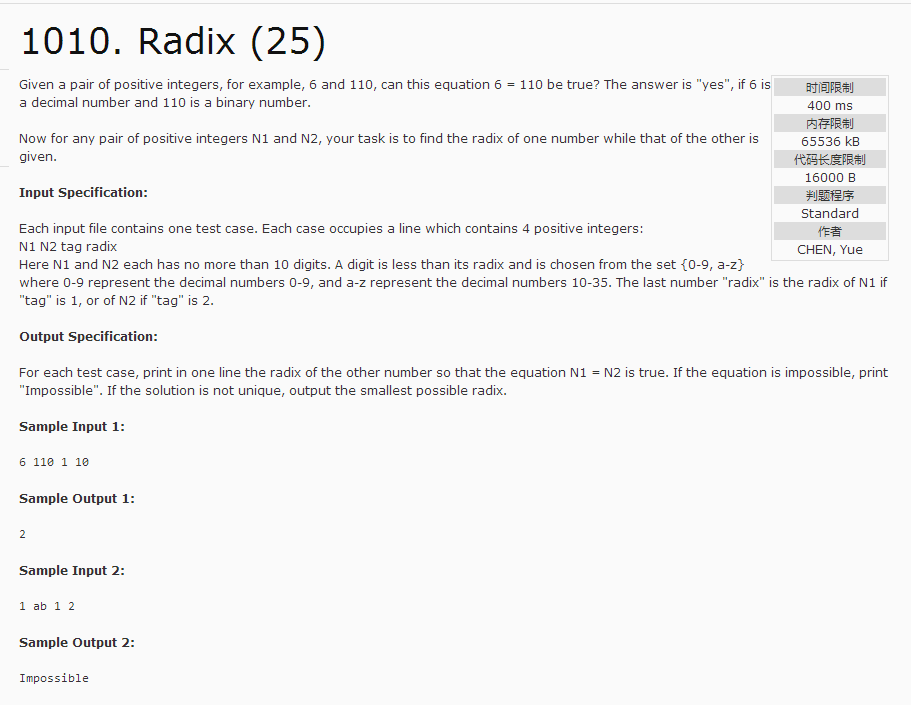
Given a pair of positive integers, for example, 6 and 110, can this equation 6 = 110 be true? The answer is yes, if 6 is a decimal number and 110 is a binary number.
Now for any pair of positive integers N1 and N2 , your task is to find the radix of one number while that of the other is given.
Input Specification:
Each input file contains one test case. Each case occupies a line which contains 4 positive integers:
N 1 N 2 t a g r a d i x N_1 N_2 tag radix N1 N2 tag radix
Here N1 and N2 each has no more than 10 digits. A digit is less than its radix and is chosen from the set { 0-9, a-z } where 0-9 represent the decimal numbers 0-9, and a-z represent the decimal numbers 10-35. The last number radix is the radix of N1 if tag is 1, or of N2 if tag is 2.
Output Specification:
For each test case, print in one line the radix of the other number so that the equation N1 = N2 is true. If the equation is impossible, print Impossible. If the solution is not unique, output the smallest possible radix.
Sample Input 1:
6 110 1 10
Sample Output 1:
2
Sample Input 2:
1 ab 1 2
Sample Output 2:
Impossible
这道题的陷阱就是很多人以为进制固定在2-36进制,其实不然,要用二分查找符合条件的进制,下限即为字符串最大的字符+1(注意下限最小为2),上限就是确定进制的字符串的十进制,注意本题卡int,故须判断一下上界是否溢出。我写得尽可能简洁易懂,供大家参考,AC代码如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ans1=0,ans2=0;
int n,k;
string s1,s2;
ll p(ll k,int t){//手写pow函数,防止其越界ll s=1;for(int i=0;i<t;i++){s*=k;}return s;
}ll sum(string s,ll k){//k进制转十进制int len=s.length();ll ans=0;for(int i=0;i<len;i++){if(isdigit(s[i])) ans+=p(k,len-i-1)*(s[i]-'0');else ans+=p(k,len-i-1)*(s[i]-'a'+10);}return ans;
}ll maxnum(string s){//找二分查找的下限int len=s.length();int ans=0;for(int i=0;i<len;i++){if(isdigit(s[i])) ans=max(ans,(s[i]-'0'));else ans=max(ans,s[i]-'a'+10);}return ll(ans+1);
}ll bs(string s,ll a){//二分查找ll l=maxnum(s),r=max(a,l);if(l<2) l=2;//稳定下界,但是后来试了一下,不加也是对的,看来数据还没那么坑while(l<=r){ll mid=(l+r)/2;ll ans=sum(s,mid);if(ans==a) return mid;else if(ans>a || ans<0) r=mid-1;//ans<0很重要,检查上界是否溢出else l=mid+1;}return -1;
}void judge(){ans1=sum(s1,k);ll p=bs(s2,ans1);if(p!=-1){cout<<p;return;}else{cout<<"Impossible";return;}
}int main(){cin>>s1>>s2>>n>>k;if(n==2) swap(s1,s2);judge();return 0;
}