最近在看ICDE2021的调优文章时发现出现了大量的Pareto Set的理论,这里记录一下。
一、Pareto理论
由意大利经济学家维弗雷多·帕雷托 (Villefredo Pareto)(图1)在1987年提出:社会财富的80%是掌握在20%的人手中,而余下的80%的人只占有20%的财富。这个概念被延伸到别的社会领域,得到了帕累托理论,即对于大多数的结果,大约80%的后果来自20%的原因。这也就指出大多数情况下都存在“关键的少数”群体,这个理论也被称为80/20理论。

图1 Pareto(图源百度百科)
帕累托现象在数学上可以由一种特定参数的幂律分布来描述。许多现实中的情况都符合该理论的描述,一个常见的帕累托现象是生活中大多数企业80%的收入都来自于20%的关键客户。
二、Pareto最优
帕累托最优指一种多目标优化的特定情况,在这种情况下,不存在不损害其余目标标准的条件下使某一个目标的标准提高的情况。这个理论在博弈论中得到了很好的应用。
我在另一篇博客里找到了一个很好的例子:
举例1:假设现在有两个人,甲和乙,分10块蛋糕,并且两个人都喜欢吃蛋糕。10块蛋糕无论在两个人之间如何分配,都是帕累托最优,因为你想让某一个人拥有更大利益的唯一办法是从另一个人手里拿走蛋糕,导致的结果是那个被拿走蛋糕的人利益受损。
举例2:假设现在有两个人,甲和乙,分10块蛋糕10个包子。甲喜欢吃蛋糕而乙喜欢吃包子,而且甲讨厌吃包子,乙讨厌吃蛋糕(甲包子吃得越多越不开心,乙蛋糕吃得越多越不开心)。这种情形下,帕累托最优应当是:把10块蛋糕全部给甲,把10个包子全部给乙。因为任何其他的分配都会使得至少一个人手里拿着一些自己讨厌的东西,比如甲拥有10块蛋糕以及2个包子,乙拥有8个包子。这个时候,如果把2个包子从甲的手里转移到乙的手里,甲和乙都变得比原来更开心了,同时这样的转移并不会使得任何一方的利益受损。
三、Pareto解
针对多目标优化问题,往往存在针对某个目标是最优的条件,对于其他目标反而表现不佳的情况。即加入我们有一组目标函数,最佳的解往往不唯一,且优化其中某个函数时,往往会削弱其他的函数表现。
我们把符合Pareto最优的这些解的结合称为Pareto最优集,在超空间中形成的超曲面称为Pareto frontier或Pareto set。
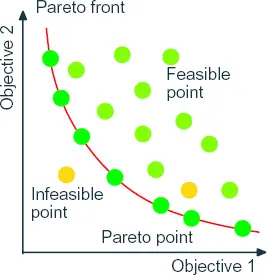
图2 一种Pareto front
拿上面的举例一来说明,我们令X,Y为甲和乙的蛋糕数,则解集c:(0,10), (1,9), ...,(10,0)都是满足Pareto最优的解,则c就是Pareto set,而这条二维空间中的曲线就是Pareto frontier。
在计算机领域,Pareto原理可以用于优化问题的描述。例如微软这篇文章指出,优化20%的代码可以解决系统中80%的问题。