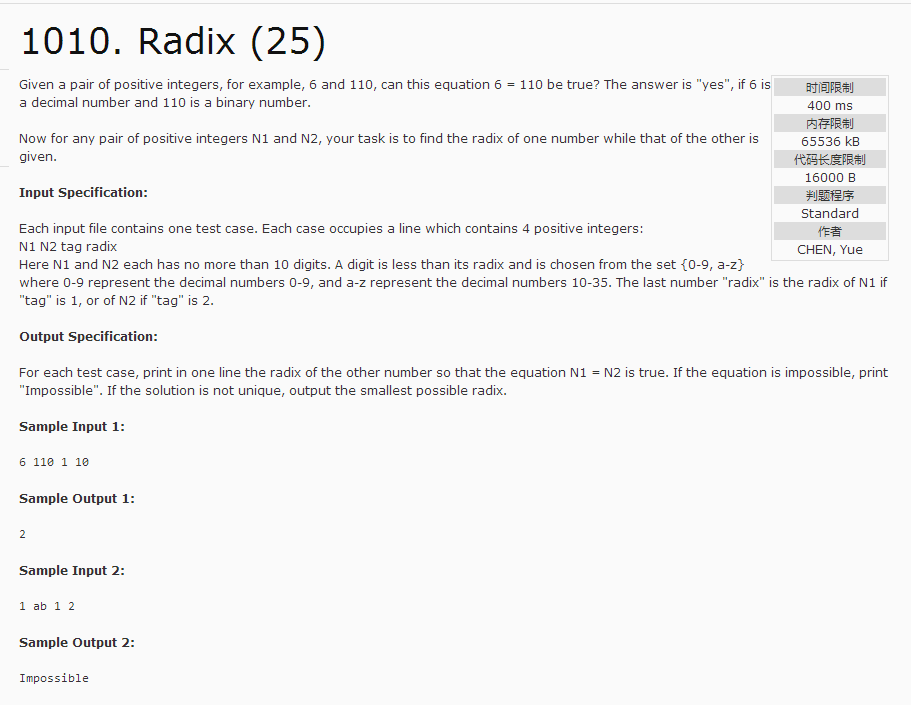
1010 Radix (25 分)

今天给大家分享的是PAT甲级的一道小题，求进制。

原题请点击我

简单翻译：

给你两个数字，告诉你一个数的进制是多少，问，另一个数是否在某个进制下和第一个数相等。如果存在，就输出这个进制，如果不存在，就输出不存在。

思路：

提示1：

把两个数都转换成10进制数，如果存在转换后相等的，那么就找到了相等的条件。

提示2：

10进制的中只能存在0 ～ 9。n进制中，只能存在0 ～ n - 1。

提示3：

同一个数，把他看成n进制再转换为10进制求得的10进制数，一定比看成n + 1进制再转换为10进制求得的10进制数要小。

提示4：

这个数可能本身并不大，但是如果把他看作一个很大的进制表示的数的话，那么他转换成10进制后就会非常大。具体来说，1如果看作是10000000000进制表示的话，转换成10进制就是10000000000。

提示5：

题目中给出的数，不包含负数，不含小数，最小的进制是2进制，不存在负数的进制或者0，1进制。

具体的思路：

这个问题是整个A组题里通过率最低的题

Q：这个题通过率最低，那他是最难的吗？
A：并不是。
Q：既然不是最难的，为什么通过率最低呢？
A：因为他不给数据范围。

先吐槽到这儿，上面给的五个提示是针对这个问题的思路以及坑的地方。下面来具体介绍思路：

我们的思路是，将给定的那个数先转换成10进制，再遍历其他进制，让另一个数按照那个进制转换成10进制后，如果能让两数相等，那么就能找到解。
既然是循环，就要有起点和终点，根据提示2，我们可以找到左边界，从左边界开始不停的遍历即可。
暴力循环会超时。再根据提示3，可以想到二分的方案，不同的进制对应的结果是递增的，所以可以拿进制来进行二分。
二分依然会被卡，原因是二分到最后，进制可能会非常大，虽然在为数不多的给出的范围中，给了数据最多有10位，但是这10位在高进制的运算下依旧可能非常大，超过了long long 的范围。怎么处理呢？
如果某次运算的结果，出现了以某个进制转换过后是一个负数，那么最终的结果一定在二分的左半部分，右边就不考虑了。这样的话就可以处理溢出的情况了。

知道了这些，代码就可以写出来了。

C++ 代码：

#include"bits/stdc++.h"
#define all(x) x.begin(),x.end()
#define len(x) x.size()
#define INF (1e15)
#define vi vector<int>
#define ll long long int
#define ull unsigned long long int
#define db double
#define vvi vector<vector<int>>
#define pb(x) push_back(x);
#define MAXN 100
using namespace std;
//k进制的s转换成10进制的数字
ll f(string s, ll k) {ll ans = 0;for (int i = 0; i < len(s); i++) {ll num;if (s[i] >= 'a') num = s[i] - 'a' + 10;else num = s[i] - '0';ans = ans * k + num;}return ans;
}
int main() {string N[2];int tag;ll radix;cin >> N[0] >> N[1] >> tag >> radix;ll num1 = f(N[tag - 1], radix);//找最小进制,即找最大的数，int m = 0;for (int i = 0; i < N[2 - tag].size(); i++) {int temp = 0;if (N[2 - tag][i] >= 'a') {temp = N[2 - tag][i] - 'a' + 10;} else {temp = N[2 - tag][i] - '0';}m = max(m, temp);}ll l = max(m + 1, 2), r = INF;while (l < r) {ll mid = l + (r - l) / 2;//cout << "haha" <<  f(N[2 - tag], mid) << endl;ll temp = f(N[2 - tag], mid);if (temp >= num1 || temp < 0) {r = mid;} else {l = mid + 1;}}if (f(N[2 - tag], l) == num1) {cout << l << endl;} else {cout << "Impossible" << endl;        }return 0;
}