图(Graph)的定义
文章目录
- 图(Graph)的定义
- ●图的形式化定义:G = (V,E)
- ●无向图和有向图的表示形式:
- ● 有向图和无向图的定义
- ●抽象数据类型定义ADT
●图形结构属于复杂的非线性结构
● 图由顶点的集合和边的集合构成
●图的形式化定义:G = (V,E)

• 集合V(vertex):顶点的有限集合,记为V(G)
▪ 对于n个顶点的图,对每个顶点连续编号,即顶点的编号为0 ~ n-1
▪ 通过编号唯一确定一个顶点
• 集合E(Edge):连接V中两个不同顶点(顶点对)的边的有限集合,记为E(G).
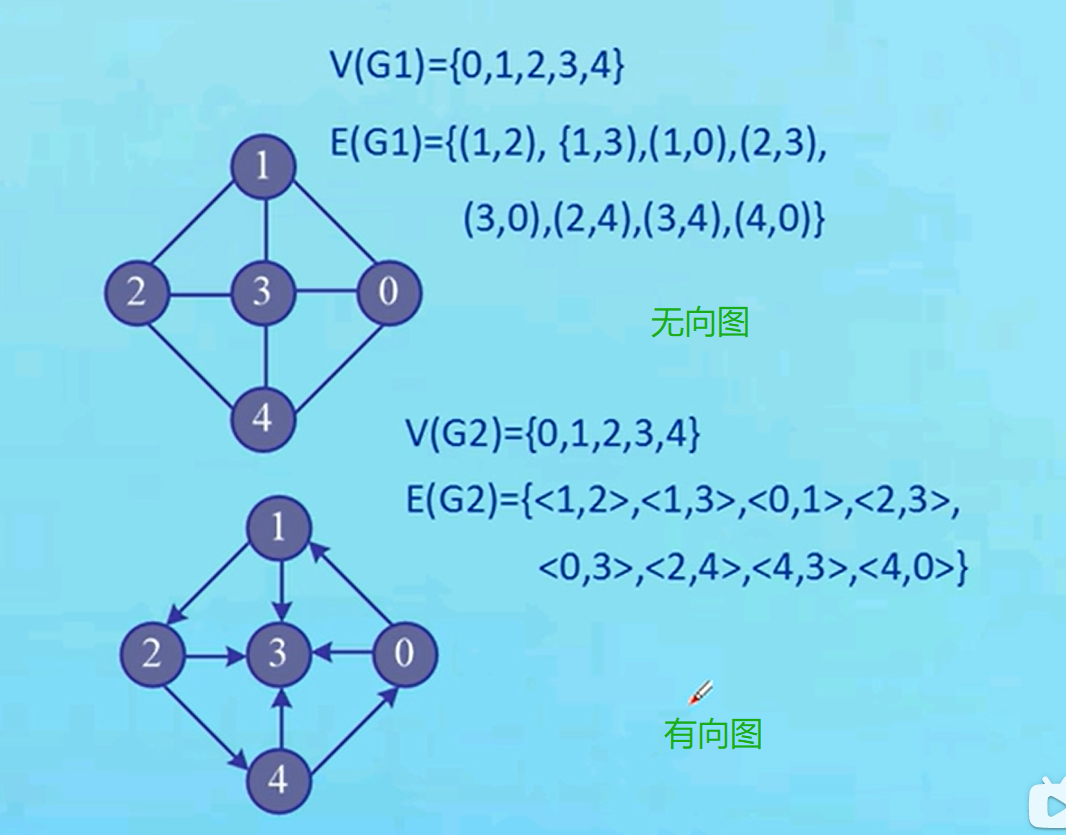
●无向图和有向图的表示形式:
①无向图,如图所示

②有向图,区别就是括号变成尖括号,左右两个顶点分别表示起点和终点.
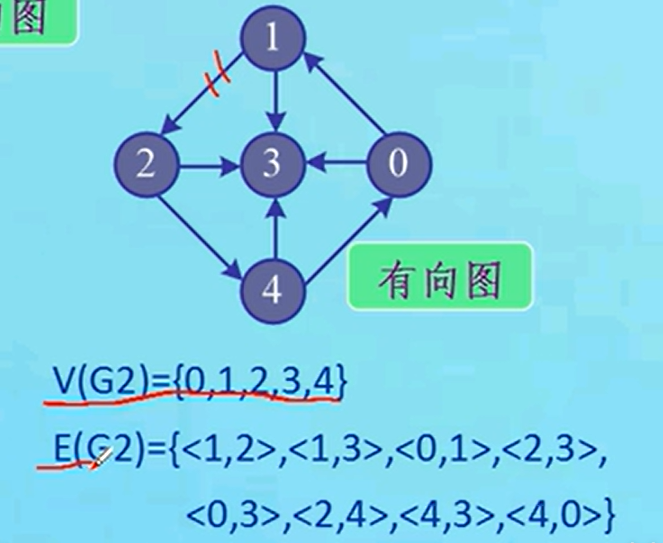
● 有向图和无向图的定义
♥ 无向图
• 边之间的"顶点对"是无序的,则称图G为无向图.
• (i,j)表示一条无向边,和(j,i)是同一条边。
♥ 有向图
• 边之间的顶点对是有序的,则称G为有向图
• <i,j>∈E(G)表示由i到j方向有一条边
●抽象数据类型定义ADT
ADT Tree
{
数据对象:
D={ai|aiElemType, i=1,2,3…,n,n>=0} //ElemType为类型标识符
数据关系:
R = {<ai,aj>ai,aj∈D, i=1,2,…,n,j=1,2,…,n,其中每个元素可以有零个或多个前驱节点,可以有零个或多个后继节点}
数据关系:
(1)初始化图InitGraph(&g):构造一个空的图g
(2)销毁图ClearGrapth(&g):释放图g所占用的空间
(3) DFS(G,V):从顶点v出发,深度优先遍历图g
(4) BFS(G,V):从顶点v出发,广度优先遍历图g
…
}
思考:其实图所对应的顶点和边的关系, 也是对应了数据结构里面数据对象和数据关系.