1，主成分分析

主成分分析（Principal Component Analysis，PCA）是一种无监督问题，是降维中最常用的一种手段，基于方差（方差最大的方向）提取最有价值的信息再进一步分类。降维后数据特征的意义发生变化。

2，向量的表示及基变换

2.1 内积：
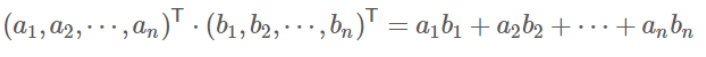设向量B的模为1，则A与B的内积值等于A向B所在直线投影的矢量长度：

2.2 向量的线性组合

向量可以表示为(3,2)实际上表示线性组合：

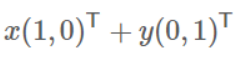
其中(1,0)和(0,1)叫做二维空间中的一组基

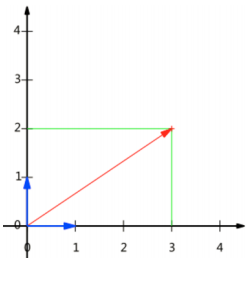
2.3 基变换

基是正交的（即内积为0，或直观说相互垂直，线性无关），更好的表达坐标轴上的数据。

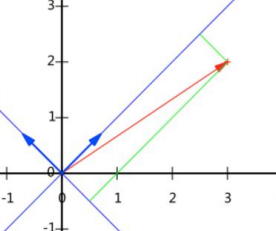
变换：数据与一个基做内积运算，结果作为第一个新的坐标分量，然后与第二个基做内积运算，结果作为第二个新坐标的分量，比如：

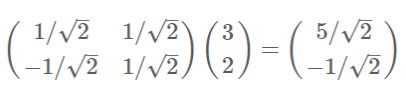
推广到多维：

两个矩阵相乘的意义是将右边矩阵a中的每一列列向量ai变换到左边矩阵p中每一行行向量pi为基所表示的空间中去（尽可能去除线性相关性）。

2.4 协方差矩阵

方向：选择的这个方向（或者说基）应该尽量保留最多的原始信息，即一种直观的看法是：希望投影后的投影值尽可能分散。

方差（单个特征发散的程度）：

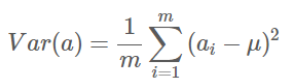
寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大（尽可能分散）

协方差（假设均值为0时（以0为中心化），两个特征之间的关系）：

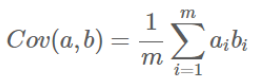
如果单纯只选择方差最大的方向，后续方向应该会和方差最大的方向接近重合。而为了让两个字段尽可能表示更多的原始信息，我们是不希望它们之间存在（线性）相关性的，可以用两个字段的协方差表示其相关性，当协方差为0时，表示两个字段完全独立。为了让协方差为0，选择第二个基时只能在与第一个基正交的方向上选择，然后在保证第二个基在该方向上的方差尽可能大。因此最终选择的两个方向一定是正交的。

3，优化目标

将一组N维向量降为K维（K大于0，小于N），目标是选择K个单位正交基，使原始数据变换到这组基上后，各字段两两间协方差为0，字段的方差则尽可能大。

协方差矩阵：

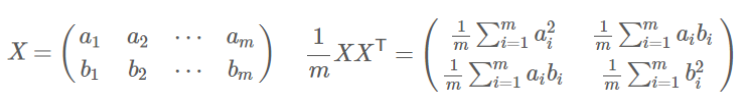m代表数据的个数，x为数据本身，矩阵对角线上的两个元素分别是两个字段各自的方差，而其它元素是a和b的协方差

协方差矩阵对角化：即除对角线外的其它元素化为0（协方差为0），并且在对角线上将元素按大小从上到下排列（方差尽可能大）

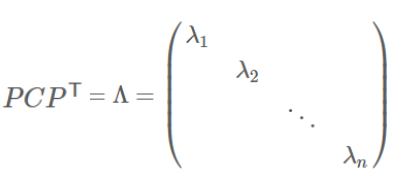
一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量：

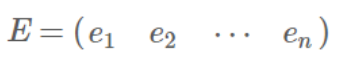
实对称阵可进行对角化：

根据特征值的从大到小，将特征向量从上到下排列，则用前K行组成的矩阵乘以原始数据矩阵X，就得到了我们需要的降维后的数据矩阵Y

4，PCA实例

（1）原始数据共5个数据，每个数据有2个特征，并进行0中心化
（2）计算协方差矩阵，对角线为特征的方差，非对角线为特征的协方差（特征间的关系）：
（3）进行矩阵分解求特征值和特征向量，找出对应特征值最大的特征向量，并对该向量进行归一化处理（基）
（4）将基向量与原始数据作内积得到降维后的结果
5，线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA）是由Ronald A. Fisher在1936年提出了线性判别方法，用于数据预处理中的降维，完成分类任务，LDA关心的是能够最大化类间区分度的坐标轴成分，即将特征空间（数据集中的多维样本）投影（找到更合适分类的空间k）到一个维度更小的 k 维子空间中，同时保持区分类别的信息。所以与PCA不同，LDA更关心分类而不是方差。

5.1 原理
LDA是“有监督”的，它计算的是另一类特定的方向，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近方法
原始数据：

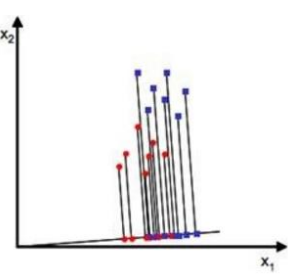
找到合适的空间进行投影：

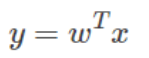
变换数据（投影后的数据）：

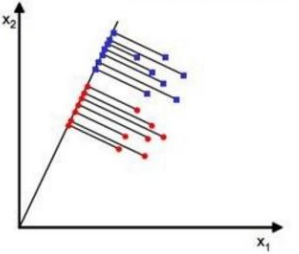
从上述来看，LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好。

每类样例的均值：

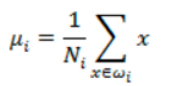
投影后的均值：

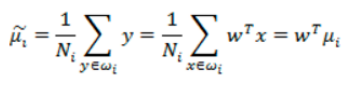
投影后的两类样本中心点尽量分离：

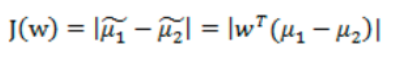
但是只是最大化J(w)，并不能满足要求，如下图，X1的方向可以最大化J(w)，但是却分的不好

散列值描述了样本点的密集程度，值越大，越分散，反之，越集中。同类之间应该越密集些：

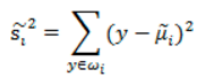
故目标函数为：

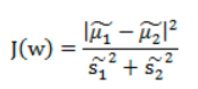
散列值公式展开：

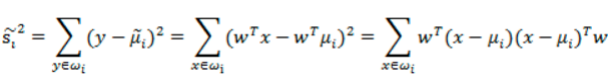
散列矩阵：

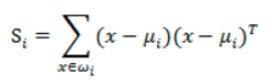
类内散布矩阵Sw = S1+S2：

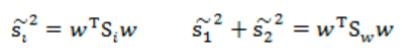
目标函数的分子展开：
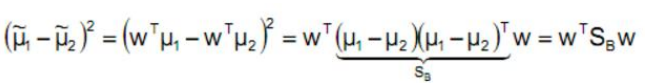??称作类间散布矩阵，故最终目标函数：

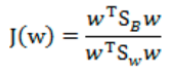
分母进行归一化，如果分子、分母是都可以取任意值的，那就会使得有无穷解，故将分母限制为长度为1

拉格朗日乘子法：

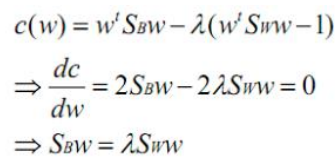
两边都乘以Sw的逆：