利克瑞尔数(Lychrel Number)指的是将该数与将该数各数位逆序翻转后形成的新数相加、并将此过程反复迭代后，结果永远无法是一个回文数的自然数。

  逆序并相加的过程是将一个数的各位逆序排列后再与原数相加，而得到两者之和。例如: 56 + 65 = 121, 125 + 521 = 646, 9999 + 9999 = 19998。在将这种逆序相加的过程重复几次后，对有些数来说可以很快地得到一个回文数的结果，这样的数就不是利克瑞尔数。 经过这样的重复，所有一位数和两位数最终都得到了回文数的结果。10,000以下的数中，大约 80% 的数会在四步以内的迭代后形成回文数;统共大约 90% 会在七步以内形成回文数。

  

这里有一些非利克瑞尔数的例子:

56 在一次迭代后形成回文数:56+65 = 121.

57 在两次迭代后形成回文数:57+75 = 132, 132+231 = 363.

59 也不是利克瑞尔数，因为在三次迭代后也得到了一个回文数结果:59+95 = 154, 154+451 = 605, 605+506 = 1111

89 经过少有的24 次迭代(它是 10,000 以下的数中迭代次数最多的)而得到回文数 8813200023188.

10,911 最后得到回文数 4668731596684224866951378664，经过 55 次迭代.

1,186,060,307,891,929,990 花费了 261 次迭代 而形成一个 119 位数的回文数。

  下面是相关代码：

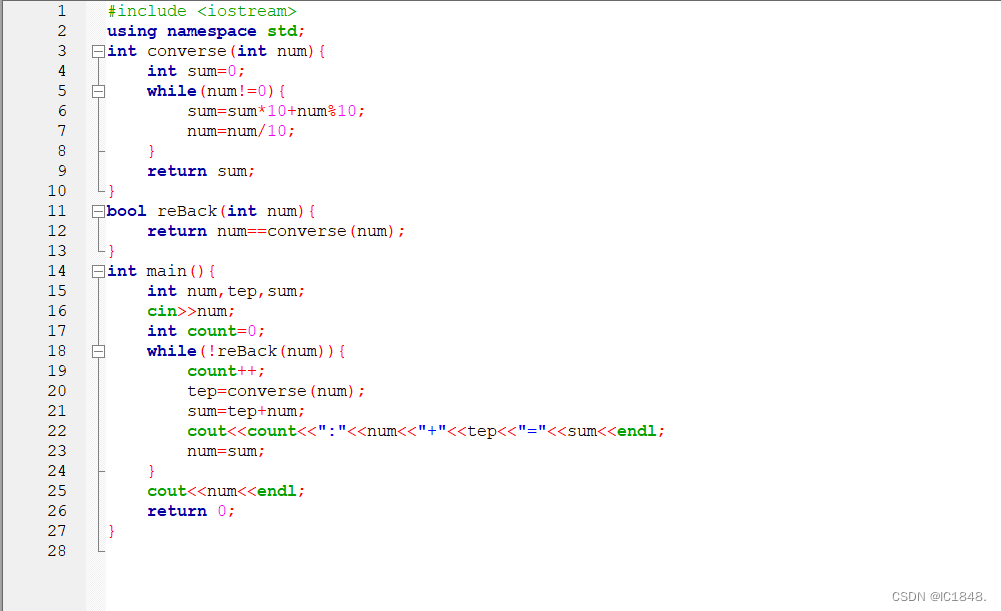
希望对大家有所帮助