A Unified Solution to Constrained Bidding in Online Display Advertising:一种对在线展示广告约束出价问题的通用解决方案 未开放但是可以搜到
NeuralAuction: 电商广告中的端到端机制优化方法 https://arxiv.org/abs/2106.03593
一种使用真负样本的在线延迟反馈建模 https://arxiv.org/abs/2104.14121
广告主端的“猜你喜欢”:在线广告投放策略推荐系统 https://arxiv.org/abs/2105.14188
基于多智能体协同竞价博弈的电商搜索广告多目标竞价优化 https://arxiv.org/abs/2106.04075
基于深度置信度感知学习的广告投放探索方案 https://arxiv.org/abs/2012.02298
A Unified Solution to Constrained Bidding in Online Display Advertising
一种对在线展示广告约束出价问题的通用解决方案
摘要:本文提出了一种通用的解决方案,以解决在线展示广告中的约束出价问题。在在线展示广告领域,广告主通常通过实时竞价来获得曝光机会。然而,在大多数广告平台中,广告主最常见的需求是在预算和某些KPI约束下,最大化竞得流量的价值,例如,在预算和点击成本约束下,最大化点击量。不同的广告主有着不同的投放需求,这些需求在营销目标(如点击、曝光)、KPI约束类型(如点击成本上限、点击率下限)以及KPI约束数量三个维度上存在很大差异。现有研究通常仅针对某一特定需求,缺乏通用性,因此很难达到最优的投放效果。本文的目的是提供一种通用的解决方案,使得广告主能够在各种不同的约束条件下最大化竞得流量的价值。
本文通过将广告主的投放需求形式化为约束出价问题,并推导出统一的最优出价策略,提供了一种解决在线展示广告中约束出价问题的通用解决方案。该方案的最优出价公式包含m个参数,其中m为约束数量。为了解决实际应用中竞争环境不断变化导致的确定最优出价参数的难题,本文还提出了一种强化学习方法,该方法能够在投放过程中动态调整出价参数,使其尽可能逼近最优参数。通过对强化学习过程进行优化,使其能够更快地收敛到最优解。该方法被称为“统一约束出价在线解决方案”(USCB)。实际应用中,USCB已在阿里妈妈广告投放策略平台上得到了部署,为各个业务线提供出价参数调控服务,为平台带来了显著收益增长和广告主的投放效果提升。
摘要:
在在线展示广告中,广告商通常通过实时竞价获取广告展示机会。在大部分广告平台上,广告商的典型需求是在预算和关键绩效指标约束下最大化获得展示的总价值(例如,在预算和每次点击成本上限的约束下最大化点击次数)。这类需求在价值类型(如广告曝光/点击)、约束类型(如每单位价值的成本)和约束数量上有所不同。现有研究通常关注特定需求,或难以实现最优。在本文中,我们将此需求形式化为一个有约束的竞价问题,并推导出一个代表广告商的统一最优竞价函数。最优竞价函数使得广告商仅需使用m个参数(即约束数量)就能为所有展示计算出竞价。然而,在实际应用中,由于拍卖环境的非稳定性,确定参数并非易事。我们进一步提出了一种强化学习(RL)方法,以动态调整参数实现最优,递归优化特性显著提高了收敛效率。我们将这个公式和RL方法统称为“受约束竞价的统一解决方案”(USCB)。USCB已在工业数据集上验证其有效性,并已在阿里巴巴展示广告平台上投入使用。
CCS概念:
信息系统 → 计算广告;展示广告
关键词:
实时竞价;展示广告;竞价优化
1引言
近年来,网络展示广告已发展成为最具影响力的行业之一,2019年美国的收入高达598亿美元[13]。实时竞价(RTB)在在线展示广告领域取得了巨大成功[19, 24],广告商们需要针对每一个广告展示机会提交竞价。最高出价者将获得广告展示机会,支付的费用则为次高出价。这种分配和支付规则被称为第二价格拍卖(SPA),在在线展示广告行业中发挥着重要作用[8]。
当前,参与在线展示广告拍卖的广告商主要有两类:品牌广告商和效果广告商[20]。品牌广告商关注长期增长和知名度,他们制定广告活动,目标通常是在一定约束条件下向尽可能多的受众展示广告。这些约束条件通常与“浅层”绩效指标有关,如每次展示/点击的平均成本。而效果广告商则试图在一些“深层”绩效指标的约束下最大化赢得展示的总价值,例如在平均每次转化成本约束下最大化转化次数。为了满足这些需求,广告平台通常为客户提供相应的竞价策略,如谷歌、脸书和阿里巴巴[2, 9, 11]。
现有研究通常关注解决特定问题以满足广告商的不同需求。例如,文献[21, 23]尝试在一个和两个约束条件下优化广告活动的目标。然而,约束条件在类型和数量上通常是多样的,可能涉及一个或多个不同的关键绩效指标(KPI),包括但不限于预算、千次展示成本(CPM)、每次点击成本(CPC)、每次行动成本(CPA)、投资回报率(ROI)、点击率(CTR)和每次展示转化(CPI)。尽管文献[16]试图提供一个统一的解决方案,但竞价函数并非最优,因为它旨在最小化KPI误差,在KPI约束不合适时(例如在100美元预算和100美元CPC约束下最大化点击次数)可能导致糟糕的结果。因此,设计一个统一的解决方案以最优地满足各种广告商需求并适用于现实世界的广告系统具有重要意义。
在本文中,我们深入挖掘在线展示广告广告商的核心需求,并通过线性规划[6]将其构建为一个受约束的竞价问题。具体而言,广告活动的核心目标是在一个或多个约束条件下,如预算约束和关键绩效指标约束,最大化赢得展示的总价值。为了让每个广告活动都能参与拍卖并充分利用实时竞价的流动性,我们采用原始-对偶方法[3]为受约束的竞价问题推导出一个统一的最优竞价函数。最优竞价函数由m个核心参数决定,其中m是约束条件的数量。
然而,确定核心参数并非易事。由于展示在一天内按顺序到达,提前在没有完整展示集的情况下计算核心参数具有很大挑战性。同时,从特定广告活动的角度来看,拍卖环境是动态且不可预测的[21]。因此,历史数据中的核心最优参数可能与实际最优参数有很大偏差。因此,我们将其视为基于受约束竞价基本表述的顺序参数调整问题,并尝试通过强化学习(RL)[15]解决这个问题。得益于受约束竞价表述中的递归优化特性,收敛效率得到显著提高。
为了评估我们的解决方案在受约束竞价问题中的有效性和通用性,我们首先构建了基于现实世界的工业数据集,然后将我们的方法与针对三个不同受约束竞价问题的最先进方法进行比较。实验结果表明,我们的方法明显优于其他方法。
我们的贡献可以概括为以下三个方面:
• 在我们所知范围内,这是首个为在线展示广告中受约束的竞价问题推导出统一最优竞价函数的研究。
• 我们提出了一种基于强化学习的方法来搜索关键参数调整策略,这一策略具有通用性、工业适用性和有效性。
• 基于现实世界工业数据集的实证评估证实了我们解决方案的有效性。此外,该解决方案已在淘宝展示广告系统中部署并得到验证。
本研究的其余部分安排如下:第2节描述了受约束竞价问题的表述,并推导出统一的最优竞价函数。第3节提出了我们的强化学习方法。第4节讨论了实验结果,第5节介绍了相关工作。最后,我们在第6节对本文进行总结。
在本研究中,我们首次为在线展示广告中受约束的竞价问题推导出统一的最优竞价函数,并提出了一种基于强化学习的方法来搜索关键参数调整策略,这一策略具有通用性、工业适用性和有效性。实证评估表明,我们的解决方案在现实世界的工业数据集上表现优越,优于其他方法。除了实验之外,这个解决方案已经在淘宝展示广告系统中部署并得到验证。我们相信,本文提出的方法对于在线展示广告领域的受约束竞价问题具有重要意义,并将为广告商和广告平台带来实际优势。
-
在实际应用中,可能有很多展示次数的点击成本(CPC)低于100美元,因此在最大化点击次数的情况下,实际CPC会显著降低。
2.1 我们来详细描述一下这个问题。
在一个特定的时间段内,如一天,假设有N个展示机会按顺序到达并按i进行索引。在实时竞价(RTB)系统中,广告商提交出价,实时竞争每个展示机会。如果广告活动2的出价𝑏𝑖大于其他活动的最高出价𝑐𝑖,那么该广告活动将赢得展示次数𝑖。展示机会的成本也是𝑐𝑖。
广告活动在获取展示次数过程中的一个共同目标是最大化赢得展示次数的总价值,即max Σ𝑖𝑣𝑖𝑥𝑖,其中𝑣𝑖是展示次数的价值,𝑥𝑖是广告活动是否赢得展示次数𝑖的二进制指标。此外,预算和关键绩效指标(KPI)约束对于广告活动控制广告投放性能至关重要。预算约束可以表示为Σ𝑖𝑐𝑖𝑥𝑖≤𝐵。
KPI约束较为复杂,可以分为两类。第一类是与成本相关(CR)的约束,它限制了某些广告活动的单位成本,例如CPC和CPA。第二类是非成本相关(NCR)约束,它限制了平均广告效果,例如CTR和CPI。由𝑗索引的KPI约束的统一表达式可以用等式(1)表示:Σ𝑖c𝑖𝑗𝑥𝑖/Σ𝑖p𝑖𝑗𝑥𝑖≤k𝑗(1),

编辑
添加图片注释,不超过 140 字(可选)
其中k𝑗是广告商提供的约束𝑗的上限,p𝑖𝑗可以是任何绩效指标或常数。c𝑖𝑗=𝑐𝑖1𝐶𝑅𝑗+q𝑖𝑗(1−1𝐶𝑅𝑗),其中q𝑖𝑗可以是任何绩效指标或常数,1𝐶𝑅𝑗是约束𝑗是否为CR的指标函数。为了便于理解,我们在表1中列出了一些常见类型的KPI约束。
综上所述,在考虑广告目标、预算和M个KPI约束的情况下,广告活动的共同需求可以通过(LP1)公式化为一个统一的受约束的竞价问题。
我们的目标是最大化展示次数的总价值:
maximize
𝑥𝑖 Σ𝑖𝑣𝑖𝑥𝑖
s.t. Σ𝑖𝑐𝑖𝑥𝑖 ≤ 𝐵
Σ𝑖c𝑖𝑗𝑥𝑖/Σ𝑖p𝑖𝑗𝑥𝑖≤ k𝑗, ∀𝑗
𝑥𝑖 ≤ 1 , ∀𝑖
𝑥𝑖 ≥ 0 , ∀𝑖 (LP1)

编辑
添加图片注释,不超过 140 字(可选)
目标函数:
最大化 Σ𝑖𝑣𝑖𝑥𝑖
这表示广告活动试图最大化获得展示次数的总价值,其中Σ𝑖𝑣𝑖𝑥𝑖表示广告活动中每个展示次数𝑖的价值𝑣𝑖乘以是否赢得展示次数𝑖的二进制指标𝑥𝑖之和。
约束条件:
Σ𝑖𝑐𝑖𝑥𝑖 ≤ 𝐵
这是预算约束,表示广告活动的总成本(成本𝑐𝑖乘以是否赢得展示次数𝑖的二进制指标𝑥𝑖之和)不得超过预算𝐵。
Σ𝑖c𝑖𝑗𝑥𝑖/Σ𝑖p𝑖𝑗𝑥𝑖≤ k𝑗, 对于所有𝑗
这是KPI约束,表示广告活动需满足关键绩效指标。这里,𝑗表示KPI类型,c𝑖𝑗表示广告活动中每个展示次数𝑖的KPI成本,p𝑖𝑗表示广告活动中每个展示次数𝑖的KPI绩效指标。k𝑗是广告商为约束𝑗设置的上限。
𝑥𝑖 ≤ 1 , 对于所有𝑖
这表示广告活动可以选择赢得展示次数𝑖(𝑥𝑖=1)或者不赢得展示次数𝑖(𝑥𝑖=0)。
𝑥𝑖 ≥ 0 , 对于所有𝑖
这是𝑥𝑖的非负约束,保证𝑥𝑖只能取0或1。
总之,该问题旨在最大化广告活动的总价值,同时满足预算约束、KPI约束以及其他相关约束。
[2]广告商通常构建多个广告活动来竞争展示次数。
广告活动需考虑广告目标、预算和M个KPI约束。这些需求可以通过(LP1)公式作为一个统一的受约束竞价问题进行表述。在这个问题中,广告活动试图最大化获得展示次数的总价值,同时满足预算约束、成本相关约束(例如CPC和CPA)和非成本相关约束(例如CTR和CPI)。
在实际应用中,广告商通常会构建多个广告活动以竞争展示次数。通过创建多个广告活动并针对不同展示次数进行竞争,广告商可以更好地满足各种约束条件,实现广告投放的优化。
表 1:限制投标中常见的关键绩效指标。
CTR:点击率,表示用户点击广告的比率。
CPI:每次展示的转化率,表示每次展示广告后发生购买行为的比率。
𝑅:转化产生的支付,表示用户购买商品或服务产生的付款。
𝑐𝑖:获得广告位 𝑖 的成本,表示获得一次广告展示的价格。

编辑
添加图片注释,不超过 140 字(可选)
表1:受限竞价中常见的KPI约束。
CTR表示点击率,CPI表示每次展示的转化率,𝑅表示转化中产生的支付,𝑐𝑖表示赢得展示次数𝑖的成本。
2.2 最优出价策略
理论上,我们可以通过求解线性规划问题(LP1)来获得最优的𝑥𝑖,以选择赢得的展示次数。为了获得(LP1),需要完全知道展示次数集。然而,在现实世界的应用中,由于每个展示次数𝑖是从一个流中到来,很难获得完整的展示次数集,也不切实际地准确预测即将到来的展示次数。因此,剩下的问题是如何在线决定是否赢得每个展示次数𝑖。由于展示次数的数量通常巨大,而且在到达之前很难预测展示次数的表现,所以解决这个问题并非易事。幸运的是,我们成功地为这个问题导出了一个统一的最优出价函数,它将解空间的维数显著降低到约束条件的数量,如定理2.1所示。
定理2.1. 每个展示次数𝑖的最优出价如下,这将导致(LP1)中的最优决策𝑥𝑖。
𝑏𝑖∗ = 𝑤0∗𝑣𝑖 − Σ𝑗𝑤∗𝑗(q𝑖𝑗 (1 − 1𝐶𝑅𝑗) − k𝑗p𝑖𝑗) (2)
其中, 𝑤0∗ > 0,如果约束条件𝑗与成本有关,则𝑤∗𝑗∈ [0, 1],否则𝑤∗𝑗≥ 0, ∀𝑗 ∈ [1, ..., 𝑀]。
证明. (LP1)的对偶问题如下
最小化
𝛼,𝛽𝑗,𝑟𝑗 𝐵𝛼 + Σ𝑖𝑟𝑖
满足: 𝑐𝑖𝛼 + Σ𝑗 (c𝑖𝑗 − k𝑗p𝑖𝑗)𝛽𝑗 + 𝑟𝑖 ≥ 𝑣𝑖, ∀𝑖,
𝛼 ≥ 0,
𝛽𝑗 ≥ 0, ∀𝑗,
𝑟𝑖 ≥ 0, ∀𝑖
(LP2)
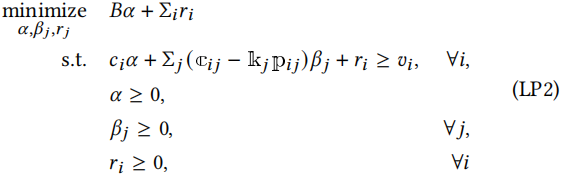
编辑
添加图片注释,不超过 140 字(可选)
其中,𝛼, 𝛽𝑗 和 𝑟𝑖 是对偶变量。
根据 c𝑖𝑗 的定义,我们可以将(LP2)中的第一个不等式重写为以下形式:
(𝑣𝑖 − Σ𝑗 𝛽𝑗 (q𝑖𝑗 (1 − 1𝐶𝑅𝑗) − k𝑗p𝑖𝑗))− (𝛼 + Σ𝑗 𝛽𝑗1𝐶𝑅𝑗)𝑐𝑖 − 𝑟𝑖 ≤ 0(3)
𝑃𝑁𝐶𝑅-𝑃𝐶𝑅
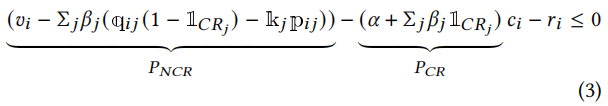
编辑切换为居中
添加图片注释,不超过 140 字(可选)
其中,𝑃𝑁𝐶𝑅表示与成本无关的系数,𝑃𝐶𝑅表示与成本相关的系数。
设原问题(LP1)的最优解为𝑥∗𝑖,对偶问题(LP2)的最优解为𝛼∗,𝑟𝑖∗和𝛽∗𝑗。
根据互补松弛定理[7],我们可以得到3:
𝑥𝑖∗(𝑃∗𝑁𝐶𝑅 − 𝑃∗𝐶𝑅𝑐𝑖 − 𝑟𝑖∗) = 0, ∀𝑖 (4)
(𝑥𝑖∗ − 1)𝑟𝑖∗ = 0, ∀𝑖 (5)
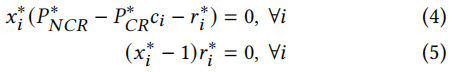
编辑
添加图片注释,不超过 140 字(可选)
我们精心地将展示次数𝑖的出价设为𝑏𝑖∗ = 𝑃∗𝑁𝐶𝑅/𝑃∗𝐶𝑅,然后我们分别将不等式(3)转换为不等式(6)和等式(4)转换为等式(7)。
(𝑏𝑖∗ − 𝑐𝑖)𝑃∗𝐶𝑅 − 𝑟𝑖∗ ≤ 0, ∀𝑖 (6)
𝑥𝑖∗[(𝑏𝑖∗ − 𝑐𝑖)𝑃∗𝐶𝑅 − 𝑟𝑖∗] = 0, ∀𝑖 (7)
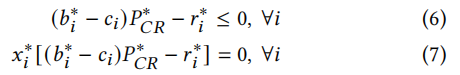
编辑
添加图片注释,不超过 140 字(可选)
可以推断出,
• 如果广告活动赢得了展示次数𝑖,即𝑥𝑖∗ > 0,根据等式(7),(𝑏𝑖∗ − 𝑐𝑖)𝑃∗𝐶𝑅 − 𝑟𝑖∗ = 0。同时,由于𝑟𝑖∗ ≥ 0,𝑃∗𝐶𝑅 ≥ 0,可以推断出𝑏∗𝑖≥ 𝑐𝑖。
• 如果广告活动输掉了展示次数𝑖,即𝑥𝑖∗ = 0,我们可以从等式(5)中推断出𝑟𝑖∗ = 0。由于𝑃∗𝐶𝑅 ≥ 0,根据不等式(6),我们可以得到𝑏𝑖∗ ≤ 𝑐𝑖。
总之,对于任何展示次数𝑖,以𝑏∗𝑖出价将导致𝑥𝑖∗,这是(LP1)的最优解。因此,最优出价是𝑏𝑖∗,为了更简洁,我们将𝑏𝑖∗的表达式组织如下,并最终完成定理2.1的证明。

编辑
添加图片注释,不超过 140 字(可选)
根据定理2.1,对于一个具有𝑀个约束条件的广告活动,希望在约束条件下最大化赢得展示次数的总价值,如等式(2)所示,最优出价由𝑀 + 1个核心参数𝑤∗𝑘,𝑘∈[0, ..., 𝑀]决定。
通过这个竞价函数,我们可以通过学习最优的𝑀 + 1个参数来处理受限竞价问题,而不是为每个展示次数分别搜索最优决策(或最优出价)。值得注意的是,参数的数量通常远小于展示次数的数量,这大大简化了问题。
当候选展示次数集合是完整的时候,可以通过求解(LP2)来计算最优参数,等式(2)中定义的最优竞价函数将导致(LP1)的相同最优解。更重要的是,当候选展示次数集合不完整时,最优竞价函数使我们能够通过调整参数接近最优解,并有助于在线决策是否赢得每个展示次数。
回顾以往的研究,[21, 25, 26]提供了一个最优竞价函数 𝑏𝑖 = 𝑤0 𝑣𝑖,在预算约束下最大化赢得展示次数的总价值,这是 𝑤𝑘 = 0, ∀𝑘 ∈ [1, ..., 𝑀] 的特殊情况;而 [23] 提出了一个最优竞价函数 𝑏𝑖 = 𝑤0 𝑣𝑖 +𝑤1 k𝐶𝑃𝐶 CTR𝑖,在预算和 CPC 约束下最大化转化数量,这是 𝑣𝑖 = CPI𝑖, p𝑖1 = CTR𝑖, k1 = k𝐶𝑃𝐶 和 1𝐶𝑅𝑗= 1 的特殊情况。
[3]𝑃∗𝑁𝐶𝑅和𝑃∗𝐶𝑅分别用𝛼∗,𝑟𝑖∗和𝛽∗𝑗计算的𝑃𝑁𝐶𝑅和𝑃𝐶𝑅。
3 方法
回顾最优受限竞价策略由等式(2)定义,因此剩下的挑战是计算最优参数 𝑤∗𝑘, 𝑘 ∈ [0, ..., 𝑀]。由于流量模式在不同的天之间会发生变化,并且展示次数集在一天结束之前是不完整的,因此无法通过解决(LP2)来获得这些最优参数。因此,在应用中,基于历史展示次数数据计算初始 𝑤𝑘,有必要开发一个参数调整代理,该代理应用其策略将 𝑤𝑘 修改为当前状态下的最优值(即广告活动的广告状态,包括预算支出状态,KPI 约束满足状态等)。在本节中,我们首先将此问题表述为马尔可夫决策过程,然后我们介绍受限竞价问题的一个重要特性,最后我们通过强化学习[18]提出一种高效的策略搜索方法。
3.1 建模
我们将参数调整问题表述为马尔可夫决策过程。马尔可夫决策过程由描述广告活动状态的一组状态 S 定义,一个代理的参数调整动作空间 A = A0×A1×...×A𝑀 ⊆ R𝑀+1。在每个时间步 𝑡,代理根据当前状态 𝑠𝑡 ∈ S 生成基于其策略 𝜋 : S ↦→ A 的动作 𝑎0𝑡, 𝑎1𝑡, ..., 𝑎𝑀𝑡 ∈A,以修改 𝑤𝑘𝑡, 𝑘 ∈ [0, ..., 𝑀],然后状态根据状态转移动态 T : S ×A ↦→ Ω(S) 转换为下一个状态,其中 Ω(S) 是 S 上的概率分布集合。环境根据当前状态和代理动作的函数返回即时奖励给代理,如 𝑟𝑡: S × A ↦→ R ⊆ R。代理的目标是最大化其总预期回报 𝑅 =Σ𝑇𝑡=1𝛾𝑡−1𝑟𝑡,其中 𝛾 是折扣因子,𝑇 是时间范围。我们的建模详细描述如下:
• S : 状态是描述广告活动的信息集合。从原则上讲,这些信息应该反映时间、预算消耗和 KPI 约束满足状态,如剩余时间、剩余预算、预算消耗速度、约束 𝑗 的当前 KPI 比率(即 (Σ𝑖c𝑖𝑗𝑥𝑖/Σ𝑖p𝑖𝑗𝑥𝑖)/k𝑗)等。
• A : 在时间步𝑡,每个代理提供一个 𝑀 + 1 维动作向量 ® 𝑎𝑡 = (𝑎0𝑡, ..., 𝑎𝑀𝑡),以修改 𝑀 +1 维参数向量 ® 𝑤𝑡 = (𝑤0𝑡, ...,𝑤𝑀𝑡),通常采用 ® 𝑤𝑡+1 = ® 𝑤𝑡· (1 + ®𝑎𝑡) 的形式,其中 𝑎𝑘𝑡 ∈(−1.0, +∞),∀𝑘 ∈ [0, ..., 𝑀]。
• 𝑟𝑡: 在时间步 𝑡,设 O 是步骤 𝑡 和 𝑡 + 1 之间的候选展示次数集,那么奖励 𝑟𝑡 = Σ𝑖 ∈O𝑥𝑖𝑣𝑖,即 O 中赢得的展示次数的总价值。
通过这种建模,我们可以利用强化学习方法来学习和优化广告策略,以便在不确定的在线广告环境中实现最佳广告投放效果。
• T:我们采用无模型RL方法来解决我们的问题,所以不需要显式建模状态转移动态。
• 𝛾:我们将奖励折扣因子𝛾设置为1,因为每个广告活动需要从每日的角度进行评估。
3.2 受约束竞价的统一解决方案(USCB)
回顾我们已经推导出受约束竞价问题的最优竞价函数(2)。由于广告展示是按天顺序到达的,在每个时间步长,我们将面临一个递归优化问题,即在剩余展示中最大化获胜展示的总价值。我们证明它可以被表述为(LP1)的相同形式,代理的最优行动如下定理3.1所示。
定理3.1. 对于每个时间步长t的子问题,竞价代理的最优行动序列是将当前的®𝑤𝑡修改为最优的®𝑤𝑡∗,并在后续时间步长保持不变。
证明。在任何时间步长t,由于广告活动已经赢得了一些展示,子问题是如何从到达的展示中选择以在给定赢得展示的情况下优化全局问题(LP1)。在子问题中,展示集、目标和约束应该得到更新。具体来说,假设已经赢得的展示的价值、成本和对应的业绩分别为𝑣#、𝑐#、c#𝑗和p#𝑗,𝑗∈[1,...,𝑀],剩余展示集为O。那么子问题可以描述如下:
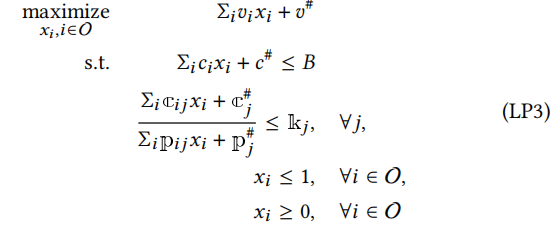
编辑
添加图片注释,不超过 140 字(可选)
(LP3)的对偶问题如下所示:
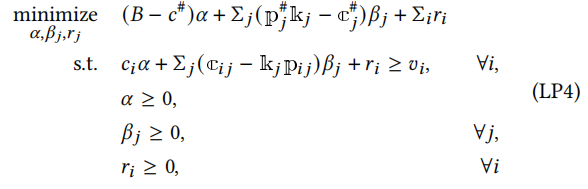
编辑
添加图片注释,不超过 140 字(可选)
,其中𝛼、𝛽𝑗和𝑟𝑖是对偶变量。
与第2.2节类似,我们可以推导出在步骤t的子问题的最优竞价𝑏∗𝑖𝑡具有与等式(2)相同的形式,即,
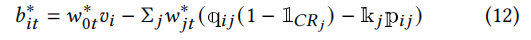
编辑
添加图片注释,不超过 140 字(可选)
,其中®𝑤𝑡∗是时间步长t的子问题的最优参数。
因此,在任何时间步长t,最优行动是将参数调整为®𝑤𝑡∗。
假设马尔可夫决策过程是确定性的,在采取最优行动后,状态将转换到一个后续状态,在该状态下,最优行动是保持参数不变。因此,在任何时间步长,最优行动序列是将当前参数调整为®𝑤𝑡∗,然后在后续时间步长保持不变。
我们在Algo. 1中提出了我们的方法,称为受约束竞价的统一解决方案(USCB)。首先,不失一般性地我们采用DDPG [17]作为我们方法的实现。其次,也是最重要的,基于Thm. 3.1,演员和评论家的学习过程得到简化,可以从以下两个方面解释:
• 在时间步长t时,代理试图一次性解决问题,即将当前的®𝑤𝑡调整为®𝑤𝑡∗并保持固定,而不是在剩余的步骤中顺序调整它。这大大降低了RL模型的学习难度。
• 评论家𝑄的学习过程简化为使G与𝑄(𝑠𝑡, ® 𝑎𝑡)之间的差异最小化,其中G是一个直接信号,用于区分哪个动作会导致问题(LP3)的更好结果,而𝑄(𝑠𝑡, ® 𝑎𝑡)是RL中的状态动作价值函数,表示在状态𝑠𝑡下采取动作® 𝑎𝑡时的预期累积价值。与更新𝑄(𝑠𝑡, ® 𝑎𝑡)以朝向𝑟𝑡 + 𝛾𝑄(𝑠𝑡+1, 𝜋(𝑠𝑡+1))的常见做法相比(更多详细信息请参阅时间差分方法[18]),𝑄的学习过程更容易,从而促进了策略收敛。
4 实验
在本节中,我们介绍实验设置并报告评估结果。最后,我们简要介绍我们方法的在线应用。我们根据三个不同的受限竞价问题进行实证研究。对于每个问题,我们将我们的方法与相应的最先进方法进行比较,并展示我们方法的优越性。优越性不仅体现在关键指标的提升上,还体现在收敛效率和合理性上。我们在淘宝广告系统中广告商最喜欢的前三个受限竞价产品上进行实验:
• CB{click}:目标是最大化点击次数,约束是预算(即Σ𝑖𝑐𝑖𝑥𝑖≤𝐵),这是在[21]中解决的问题。展示𝑖的最优竞价函数为

编辑
添加图片注释,不超过 140 字(可选)
• CB{click-CPC}:目标是最大化点击次数,约束是预算和CPC(即Σ𝑖𝑐𝑖𝑥𝑖/Σ𝑖pCTR𝑖𝑥𝑖≤k𝐶𝑃𝐶)。展示𝑖的最优竞价函数为

编辑
添加图片注释,不超过 140 字(可选)
• CB{conversion-CPC}:目标是最大化转化次数,约束是预算和CPC,这是在[23]中解决的问题。展示𝑖的最优竞价函数为
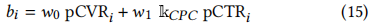
编辑
添加图片注释,不超过 140 字(可选)

编辑
OCR机翻有些地方不对

编辑
添加图片注释,不超过 140 字(可选)
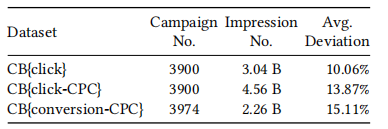
表2:三个不同受限竞价问题的数据集统计。
编辑
添加图片注释,不超过 140 字(可选)
4.1 实验设置
4.1.1 数据集。我们使用来自淘宝展示广告平台的真实竞价日志,分别为三个不同的受限竞价问题建立我们的数据集。具体来说,对于每个数据集D,每个实例可以表示为(𝑡𝑖, 𝑐𝑖𝑑, pCTR𝑖, pCVR𝑖, 𝑐𝑖),其中𝑡𝑖,𝑐𝑖𝑑, pCTR𝑖, pCVR𝑖, 𝑐𝑖分别是展示𝑖的时间戳、广告活动ID、pCTR、pCVR和竞价活动𝑐𝑖𝑑的中标价格。如表2所示,每个数据集包含3900多个广告活动和20多亿次展示,时间范围为2021年1月11日至1月23日。我们使用8天的时间窗口来确定训练、验证和测试数据集。前7天的90%数据(随机抽样)用于训练,其余10%用于验证。最后一天的数据用于测试。因此,共有6组训练/验证/测试数据集。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
图1:三个不同的受限竞标问题数据集的偏差分布。
回想一下,对于任何最优竞价函数,初始参数𝑤𝑘, ∀𝑘∈[0, ..., 𝑀] 需要事先确定。在我们的场景中,对于任何广告活动,我们使用训练数据集第7天的最优参数作为测试数据集的初始参数。我们使用等式(16)定量描述初始参数和实际最优参数之间的差异。由于在我们的数据集中𝑤0, 𝑤0∗∈R+,𝑤𝑘∈[0, 1] ∀𝑘∈[1, ..., 𝑀],我们确保分子的第一项在[0, 1]范围内,等式(16)的值域也将在[0, 1]范围内。偏差的统计数据和可视化分布如表2的最后一列和图1所示。可以看出,从广告活动的角度来看,初始参数和最优参数之间的差异可能非常大,这是由不稳定的拍卖环境造成的。

编辑
添加图片注释,不超过 140 字(可选)
, 其中, ∀𝑘∈[0, ..., 𝑀], 𝑤𝑘是训练数据集第7天的最优参数,𝑤∗𝑘是测试数据集中的最优参数
4.1.2 实现细节。我们采用一个包含3个隐藏层和每层50个节点的全连接神经网络来实现DDPG [17]的演员和评论家网络。批处理大小设置为128,重播内存大小设置为100,000。代理输出每个竞价参数的连续操作范围为[−0.2, 0.2]。代理在每15分钟采取行动,因此算法1中的时间跨度𝑇为96。对于探索随机过程,我们设置𝜇= 0和𝜎= 0.05。演员的学习速率设置为1𝑒−6,评论家的学习速率设置为1𝑒−7。在(17)中定义的KPI约束违反惩罚的超参数𝜆设置为20。在我们的案例中,最佳模型选择标准是在2000个情节内选择验证数据集上最佳的一个(度量将在下一节介绍)。在验证和测试过程中,对于每个广告活动,初始竞价参数设置为上一天数据的最优参数。通过使用GNU线性规划工具包(GLPK)来解决(LP1)的对偶问题,可以计算出最优参数。
4.1.3 评估指标。对于任何广告活动,受限竞价的目标是在一定约束条件下最大化赢得展示的总价值。设应用策略𝜋的回报为𝑅 = Σ𝑇𝑡=1𝑟𝑡,𝑅
∗为受限竞价问题的理论最优结果。原则上,度量指标应考虑以下两个方面:
• 应有一个约束违反的惩罚项。
• 只有最优策略才能实现最大值。
因此,我们将度量设计为等式(17)。惩罚项(即Σ𝑗𝑝𝑗)将在约束被违反时惩罚策略。与惩罚项一起使用的“min”运算符确保只有最优策略才能达到最大值1.0。
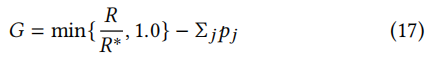
编辑
添加图片注释,不超过 140 字(可选)
其中,pj = λexrj - 1 是违反约束 j 的惩罚项,λ ∈ (1, +∞) 是惩罚强度超参数,k𝑎𝑐𝑡𝑢𝑎𝑙𝑗 = Σ𝑖c𝑖𝑗𝑥𝑖/Σ𝑖p𝑖𝑗𝑥𝑖,exrj = max{0, k𝑎𝑐𝑡𝑢𝑎𝑙𝑗/k𝑗 − 1} 表示违反 KPI 约束 j 的程度。
4.1.4 对比方法。
• 固定参数(FP):使用公式(2)进行竞价,并在测试阶段使用历史数据的最优参数保持参数固定的方法。
• 深度强化学习竞价(DRLB):[21]中提出的方法是单参数控制的最先进算法,目标是在单一预算约束下最大化展示价值。DRLB 是一种基于强化学习的方法,应用奖励塑造技术来提高收敛速度。
• 模型预测 PID(M-PID):[23]中提出的方法是双参数控制的最先进算法,目标是在预算和 CPC 约束下最大化转化数量。M-PID 基于 PID 控制器,并需要领域专家知识来确定控制目标。
• 统一约束竞价解决方案(USCB):本文提出的统一约束竞价解决方案,它抽象出约束竞价的核心需求,并用更高效的策略搜索方法加以扩展。
4.2 评估结果
我们进行实验,比较 FP、M-PID、DRLB 和 USCB 的性能。如上所述,由于实际应用中流量不稳定,测试数据中的展示量和分布偏离训练数据,这增加了竞价问题的挑战。为了研究每种方法在不同偏差下的性能,我们将所有广告活动分为 3 组,根据偏差评估每组中的四种方法。
这些方法的性能总结在表 3 中。我们的方法在与 3 种约束竞价问题相对应的所有数据集上显著优于 FP、M-PID、DRLB。此外,随着偏差的增加,所有方法的性能都会降低。我们的方法在所有偏差上都保持优势。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
表 3:在 3 个具有 3 个偏差水平的数据集中,FP、M-PID、DRLB 和我们的方法 G 的比较。
编辑切换为居中
添加图片注释,不超过 140 字(可选)
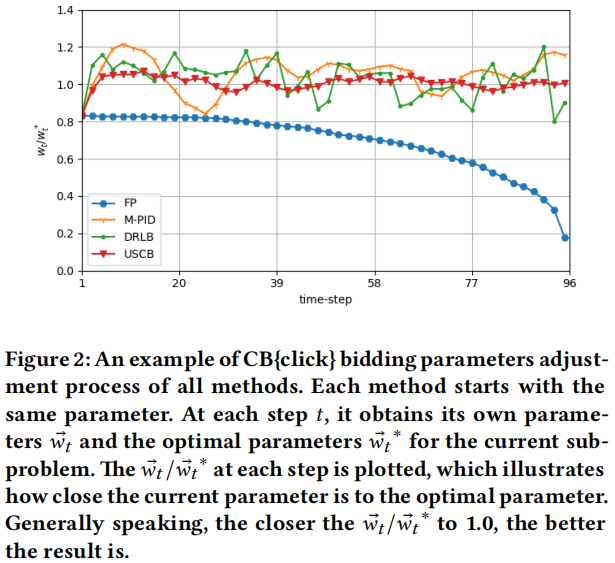
图 2:所有方法的 CB{click} 竞价参数调整过程示例。每种方法都从相同的参数开始。在每个步骤𝑡,它获得自己的参数𝑤®𝑡 和当前子问题的最优参数𝑤®𝑡∗。每个步骤的𝑤®𝑡/®𝑤𝑡∗被绘制出来,说明当前参数与最优参数有多接近。一般来说,𝑤®𝑡/®𝑤𝑡∗越接近1.0,结果越好。
为了更好地了解所有方法的性能,我们在图 2 中展示了所有方法的 CB{click} 竞价参数调整过程示例。基于这些结果,我们对这些方法进行如下分析。
• FP:FP 简单、易于实现,在拍卖环境稳定时可以取得良好结果。然而,在实际应用中,拍卖环境可能发生巨大波动,使用历史最优参数进行竞价无法保证满意的结果。如表 3 所示,由于 FP 缺乏适应环境变化的能力,导致整体效果最差。特别是,在偏差较小时,FP 获得第二好的结果,但在偏差增加时,FP 的效果最差。
• M-PID:M-PID 尝试根据当前竞价结果调整竞价参数。如图 2 所示,与 FP 相比,M-PID 能够将参数调整得更接近最优参数,因此在应对环境变化方面表现更好。然而,M-PID 存在两个方面的不足,使其在实际应用中不如强化学习方法:首先,M-PID 对每个指标设置目标至关重要。然而,设置最优目标需要专家知识。因此,M-PID 的性能不如强化学习方法,即 USCB。其次,该方法的参数搜索过程效率低下。我们需要对所有超参数进行网格搜索。搜索空间的大小与超参数的数量成指数关系。当约束数量增加时,这也会降低 M-PID 的实用性。
• DRLB:DRLB 也是一种无模型强化学习方法,理论上可以收敛到最优策略。因此,它比 FP 和 M-PID 的性能更好,这表明强化学习建模的优越性。DRLB 中提出的 rewardNet 部分解决了奖励波动的问题。然而,奖励仍受到已经学到的情节的影响,这使得其比 USCB 更加嘈杂。因此,在实践中,DRLB 的收敛速度比 USCB 慢。我们将在第 4.3 节讨论这两种方法的收敛性。
• USCB:与上述方法相比,USCB 是一种强化学习方法,经过训练可以学习在不同状态下调整竞价参数,并根据定理 3.1 进行大量简化。如图 2 所示,USCB 能够快速稳定地调整竞价参数接近最优值。因此,它在所有数据集和所有偏差中都取得了最佳性能。由于它简单、高效且有效,因此可以广泛应用于工业约束竞价问题。
总之,文中比较了四种方法在不同竞价环境中的性能。实验证明,USCB 方法在各种情况下均优于其他方法,表现出较好的适应性和效果。这些分析和结果有助于理解和应用这些方法解决实际竞价问题。
4.3 收敛效率
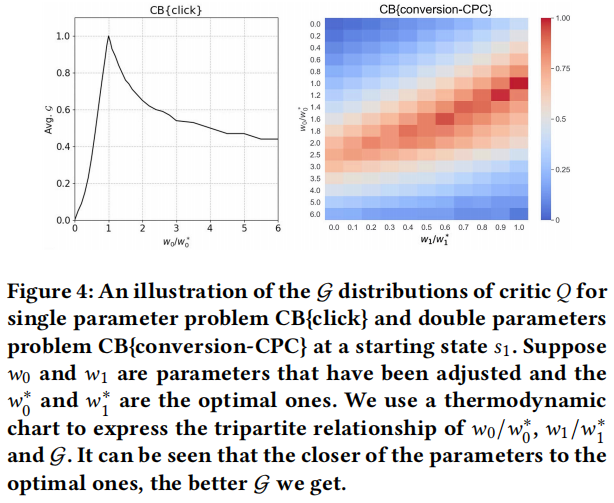
在工业应用中,为了技术迭代和降低成本,一种方法需要在可接受的时间内完成训练过程,并在部署过程中占用较少的计算资源。基于强化学习的方法通常存在收敛效率问题。为了比较 USCB 和 DRLB 的收敛效率,我们在图 3 中展示了训练过程中所有广告系列的平均指标 𝐺。可以看出,在所有数据集上,USCB 的收敛速度都比 DRLB 快。具体来说,在 CB{conversion-CPC} 数据集上,USCB 使用 1000 个训练周期达到了高于 0.9 的 𝐺 值,而 DRLB 需要至少 2000 个训练周期。
USCB 出色的收敛效率应归功于基于 Thm. 3.1 的学习过程的简化。在 Actor-Critic 框架中(本文应用的 DDPG 方法[17]基于 Actor-Critic 架构),Critic 𝑄 的准确性会直接影响 Actor 的质量[18]。根据 Thm. 3.1,在特定状态 𝑠𝑡 下,最佳动作是将当前参数调整为最优参数,并将其固定到一个周期的结束。因此,在逻辑上,𝑠𝑡 下的最佳动作应该被 Critic 𝑄 最优地评估。回想一下我们在 Algo. 1 中让 𝑄 学习 G,而 G 与我们希望在应用中优化的核心指标密切相关。G 在不同参数上的分布会直接影响 𝑄 的学习过程。为了从经验上展示 𝑄 的学习情况,我们在图 4 中展示了在 CB{click} 和 CB{conversion-CPC} 的两个特定周期的状态 𝑠1 下,G 在不同参数(动作)上的分布。我们可以看到,更好的动作(将参数调整得更接近最优参数)会获得更好的 G。因此,Critic 将快速学会区分哪个动作对 G 更好,并反过来提高 Actor 的收敛速度。

编辑切换为居中
添加图片注释,不超过 140 字(可选)
图 3:USCB 和 DRLB 在三个受约束出价问题上的训练过程。
编辑切换为居中
添加图片注释,不超过 140 字(可选)
图 4:在起始状态 𝑠1 下,Critic 𝑄 的 G 分布在单参数问题 CB{click} 和双参数问题 CB{conversion-CPC}。假设 𝑤0 和 𝑤1 是已调整的参数,𝑤0∗ 和 𝑤∗1 是最优参数。我们使用热力图来表示 𝑤0/𝑤0∗、𝑤1/𝑤∗1 和 G 的三者关系。可以看到,参数越接近最优值,我们获得的 G 值就越好。
4.4 约束违反惩罚效果讨论
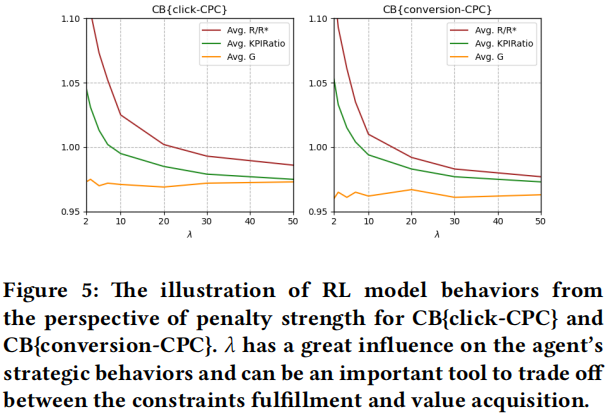
在实际应用中,由于未来展示集难以预测,参数调整策略确实可能导致 KPI 约束违反,因此,我们在指标 𝐺 中加入了约束违反惩罚项。值得注意的是,𝐺 不仅评估经验结果,还影响强化学习模型的训练过程。具体而言,超参数 𝜆 在 Eq. (17) 中对模型训练的影响值得研究。我们提取了最优 KPIRatio 为 1.0 的广告系列(这些广告系列更容易出现约束违反,RL 模型的行为会更生动),然后在图 5 中绘制了 𝜆 对 CB{click-CPC} 和 CB{conversion-CPC} 的 𝐺、KPIRatio 和 𝑅/𝑅∗ 的影响。在这些情况下,KPIRatio 是所有赢得展示的实际 CPC(即 Σ𝑖𝑐𝑖𝑥𝑖/Σ𝑖pCTR𝑖𝑥𝑖)除以广告主提供的 CPC 上限。可以看到,USCB 在几乎所有的 𝜆 下都能达到令人满意的结果(平均 𝐺 高于 0.95),即 USCB 对超参数 𝜆 具有鲁棒性。此外,当 𝜆 较小时,模型将倾向于更具侵略性,并且 KPI 违反的可能性更大。随着 𝜆 的增加,KPIRatio 变得更小,这意味着模型将更关注约束的满足。这表明 𝜆 对智能体的战略倾向具有很大的影响,可以成为我们在约束满足和价值获取之间进行权衡的重要工具。
编辑切换为居中
添加图片注释,不超过 140 字(可选)
图 5:从惩罚力度的角度展示 RL 模型在 CB{click-CPC} 和 CB{conversion-CPC} 的行为。𝜆 对智能体的战略行为具有很大影响,可以作为我们在约束满足和价值获取之间进行权衡的重要工具。
4.5 USCB 在线部署

编辑
OCR机翻有些地方不对
编辑切换为居中
添加图片注释,不超过 140 字(可选)
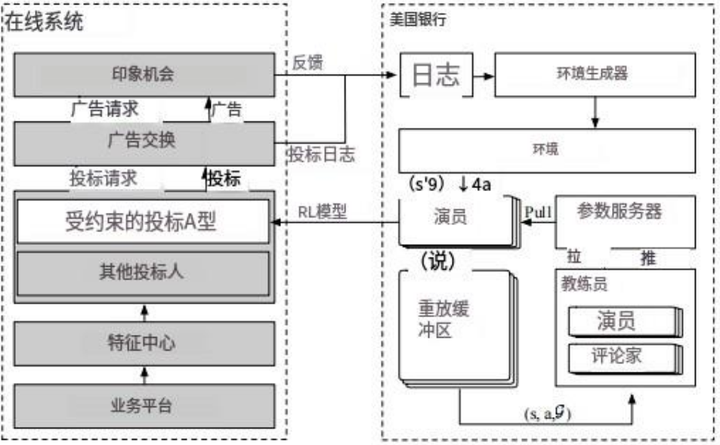
图 6:淘宝广告平台上 USCB 的部署示意图。
统一受约束出价解决方案(USCB)已在淘宝展示广告系统中部署和验证。我们的方法服务于数千家广告主,每天影响数百万的收入。算法应用的架构如图 6 所示。模型的训练和部署是并行进行的,这使得模型能够高效迭代,并且可以轻松应用于大量广告活动。
5 相关工作
在在线展示广告的实时竞价中,出价优化是一个广泛研究的问题。[29]将BCB建模为在线背包问题。[26]根据输入数据的静态分布设定出价。在[12]中,MDP用于调整展示层级出价。[4]提出了一种强化学习方法,该方法对非平稳拍卖环境具有鲁棒性。一些工作专门针对KPI约束进行了研究。[16]引入了一种通用竞价解决方案,考虑了广告价值和多个KPI约束。[23]利用反馈控制理论解决动态环境问题。[10]提出了一种机器学习方法,用于为非审查性在线首价广告拍卖建模最优出价阴影。[28]提出了一种用于首次拍卖的高效深度分布网络。与以往的工作不同,我们的工作不局限于少数约束或优化目标。我们将约束竞价问题抽象为线性规划问题,并通过原始对偶方法推导出最优竞价策略,该方法通常应用于广告分配场景[1, 5]。为了解决流量不稳定的问题,我们利用了强化学习,这已经被[14, 21]的工作证明在许多场景中是有效的。此外,展示价值估计在实时竞价场景中起着非常重要的作用,例如点击率(CTR)[27]和转化率(CPI)[22],这有助于在展示层次上精确出价。
6 结论
在本文中,我们提出了一种统一的解决方案,用于解决在线展示广告中的约束竞价问题。我们首先提取广告主的核心需求,并将其形式化为约束竞价问题。然后,我们利用原始对偶方法推导出二价拍卖下的最优竞价函数。最优函数允许广告主为所有展示量计算出价,参数数量有限。为了应对非平稳环境带来的挑战,导致连续天数之间参数偏差,我们进一步提出了一种强化学习方法来动态调整参数至最优值。更重要的是,我们发现约束竞价问题是一个递归的最优问题,这一性质显著提高了学习过程的收敛速度。我们进行了全面的实验来验证我们解决方案的有效性。我们的制定和强化学习方法一起被称为统一约束竞价解决方案(USCB),已在淘宝广告平台上部署并得到验证。
参考文献
[1] Shipra Agrawal, Zizhuo Wang, 和 Yinyu Ye. 2014. 一种用于在线线性规划的近似最优动态算法。运筹学研究62, 4 (2014), 876–890.
[2] 阿里巴巴. 2021. 阿里妈妈超级钻石。https://zuanshi.taobao.com/.
[3] Achim Bachem 和 Walter Kern. 1992. 线性规划对偶性。在线性规划对偶性中。Springer, 89–111.
[4] Han Cai, Kan Ren, Weinan Zhang, Kleanthis Malialis, Jun Wang, Yong Yu, 和 Defeng Guo. 2017. 在展示广告中通过强化学习实现实时竞价。在第十届ACM国际网络搜索和数据挖掘会议论文集中。661–670.
[5] Ye Chen, Pavel Berkhin, Bo Anderson, 和 Nikhil R Devanur. 2011. 基于性能的展示广告分配的实时竞价算法。在第17届ACM SIGKDD国际知识发现和数据挖掘会议论文集中。1307–1315.
[6] Vasek Chvatal, Vaclav Chvatal, 等。1983. 线性规划。Macmillan.
[7] A Ebrahimnejad 和 SH Nasseri. 2009. 使用互补松弛性属性解决具有模糊参数的线性规划。模糊信息与工程1, 3 (2009), 233–245.
[8] Benjamin Edelman, Michael Ostrovsky, 和 Michael Schwarz. 2007. 互联网广告和广义二次价格拍卖:出售价值数十亿美元的关键词。美国经济评论97, 1 (2007), 242–259.
[9] facebook. 2021. 在Facebook上做广告。https://www.facebook.com/business/ads.
[10] Djordje Gligorijevic, Tian Zhou, Bharatbhushan Shetty, Brendan Kitts, Shengjun Pan, Junwei Pan, 和 Aaron Flores. 2020. 首价拍卖勇敢新世界的出价阴影。在第29届ACM国际信息与知识管理大会论文集中。2453–2460.
[11] Google. 2021. 谷歌广告。https://ads.google.com/.
[12] R Gummadi, Peter B Key, 和 Alexandre Proutiere. 2011. 在预算限制下的动态拍卖中的最优竞价策略。在2011年第49届年度阿勒顿通信、控制和计算会议(Allerton)上。IEEE,588–588.
[13] IAB. 2020. 2019全年互联网广告收入报告和2020年第一季度冠状病毒对广告价格的影响报告。https://www.iab.com/video/full-year-2019-internet-advertising-revenue-report-and-coronavirus-impact-on-ad-pricing-report-in-q1-2020/。
[14] Junqi Jin, Chengru Song, Han Li, Kun Gai, Jun Wang, 和 Weinan Zhang. 2018. 通过多智能体强化学习实现展示广告中的实时竞价。在第27届ACM国际信息和知识管理大会论文集中。2193–2201.
[15] Leslie Pack Kaelbling, Michael L Littman, 和 Andrew W Moore. 1996. 强化学习:一项调查。人工智能研究杂志4 (1996), 237–285.
[16] Brendan Kitts, Michael Krishnan, Ishadutta Yadav, Yongbo Zeng, Garrett Badeau, Andrew Potter, Sergey Tolkachov, Ethan Thornburg, 和 Satyanarayana Reddy Janga. 2017. 具有多个KPI的广告投放。在第23届ACM SIGKDD国际知识发现和数据挖掘大会论文集中。1853–1861.
[17] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, 和 Daan Wierstra. 2015. 深度强化学习的连续控制。arXiv预印本arXiv:1509.02971 (2015).
[18] Richard S Sutton 和 Andrew G Barto. 2018. 强化学习:一个介绍。MIT出版社。
[19] Jun Wang 和 Shuai Yuan. 2015. 实时竞价:计算广告研究的新前沿。在第八届ACM国际网络搜索和数据挖掘会议论文集中。415–416.
[20] Christopher A Wilkens, Ruggiero Cavallo, Rad Niazadeh, 和 Samuel Taggart. 2016. 面向价值最大化者的机制设计。arXiv预印本arXiv:1607.04362 (2016).
[21] Di Wu, Xiujun Chen, Xun Yang, Hao Wang, Qing Tan, Xiaoxun Zhang, Jian Xu, 和 Kun Gai. 2018. 在展示广告中通过无模型强化学习实现预算约束竞价。在第27届ACM国际信息和知识管理大会论文集中。1443–1451.
[22] Jia-Qi Yang, Xiang Li, Shuguang Han, Tao Zhuang, De-Chuan Zhan, Xiaoyi Zeng, 和 Bin Tong. 2020. 通过流逝时间采样捕获转化率预测中的延迟反馈。arXiv预印本arXiv:2012.03245 (2020).
[23] Xun Yang, Yasong Li, Hao Wang, Di Wu, Qing Tan, Jian Xu, 和 Kun Gai. 2019. 通过多变量控制进行展示广告中的竞价优化。在第25届ACM SIGKDD国际知识发现与数据挖掘大会论文集中。1966-1974。
[24] Shuai Yuan, Jun Wang, 和 Xiaoxue Zhao. 2013. 在线广告的实时竞价:度量和分析。在第七届国际在线广告数据挖掘研讨会论文集中。1-8。
[25] Weinan Zhang, Kan Ren, 和 Jun Wang. 2016. 实时竞价最优框架讨论。arXiv预印本arXiv:1602.01007 (2016)。
[26] Weinan Zhang, Shuai Yuan, 和 Jun Wang. 2014. 面向展示广告的实时竞价最优解。在第20届ACM SIGKDD国际知识发现和数据挖掘会议论文集中。1077-1086。
[27] Guorui Zhou, Weijie Bian, Kailun Wu, Lejian Ren, Qi Pi, Yujing Zhang, Can Xiao, Xiang-Rong Sheng, Na Mou, Xinchen Luo 等。2020. CAN:重新审视点击率预测中的特征共动作。arXiv预印本arXiv:2011.05625 (2020)。
[28] Tian Zhou, Hao He, Shengjun Pan, Niklas Karlsson, Bharatbhushan Shetty, Brendan Kitts, Djordje Gligorijevic, San Gultekin, Tingyu Mao, Junwei Pan, Jianlong Zhang, 和 Aaron Flores. 2021. 面向第一价格拍卖的高效深度分布网络竞价阴影。在第27届ACM SIGKDD国际知识发现与数据挖掘大会论文集中。
[29] Yunhong Zhou, Deeparnab Chakrabarty, 和 Rajan Lukose. 2008. 面向关键字拍卖和在线背包问题的预算约束竞价。在国际互联网和网络经济研讨会上。Springer,566-576。