手撕红黑树的构建与验证

上篇文章我们介绍了AVL树的构建与适用场景，我们知道了AVL树虽然查找效率很高，但是不适合频繁插入或删除的场景。为了解决这个问题又诞生了新的数据结构：红黑树

那么本篇文章就着重介绍红黑树的性质与如何构建。

1.红黑树的性质

1.结点颜色非黑即红

2.根结点一定是红色的

3.不能有两个连续的红色结点（父和子不能同时是红色）

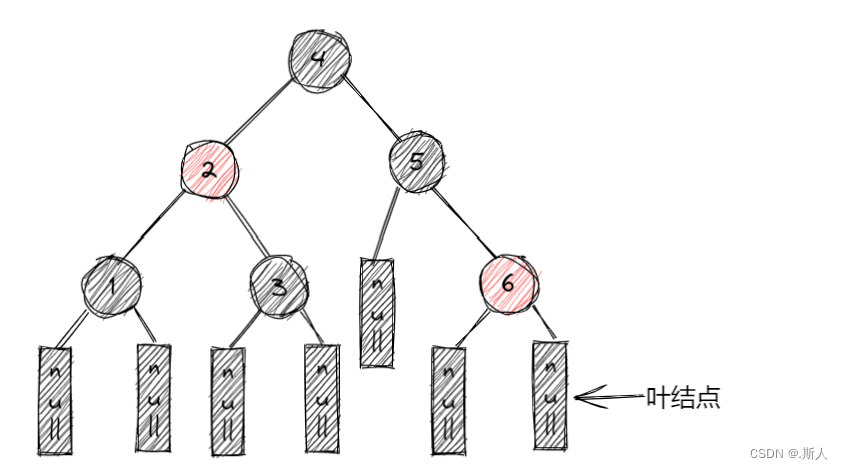
4.对于每个结点，到叶节点的每一条简单路径的黑色结点数量相同

5.叶节点是黑色的（这里的叶节点指的的空结点）

从这五个性质可以推导出来：最长路径的长度最多是最短路径的两倍

（最长路径：黑红交替，最短路径：全黑，再结合性质4就能得到推论）

举个例子：

2.红黑树的构建

因为我们是边插入边调节树结构，所以我们只要把所有的情况列举出来转换为代码即可

值得注意的是：每次我们新插入结点都默认为红色，因为在插入之前我们的树一定是满足所有性质的，一旦插入的是黑色结点，那么一定会违反性质4，所以先插入红色在考虑调整。

结点结构：
static class rbNode{int val;RBColor rbColor = RBColor.Red;//默认为红rbNode parent;rbNode left;rbNode right;}public enum RBColor {Red,Black
}
刚开始的插入和二叉搜索树的插入一样，只是插入完要分情况调节树

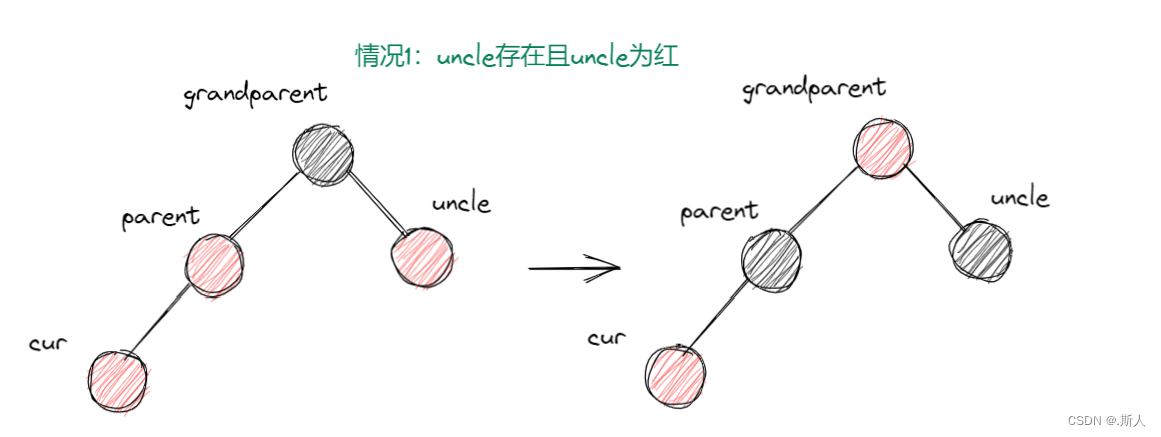
情况1

注：以下情况省略了叶子结点（null），只截取一小部分。

插入cur结点后不满足性质3，所以需要调节

parent和uncle都由红变黑

grandparent由红变黑，如果不变就违反了性质4，因为grandparent也可能存在父节点，这里只是我们没有画出。如果grandparent是根结点，最后再变为黑即可。

情况1因为grandparent是红色的所以需要继续向上调整【因为还可能不满足性质3】

情况2，3就不需要继续向上调整了

核心代码如下：
parent.rbColor = RBColor.Black;
uncle.rbColor = RBColor.Black;
grandparent.rbColor =RBColor.Red;

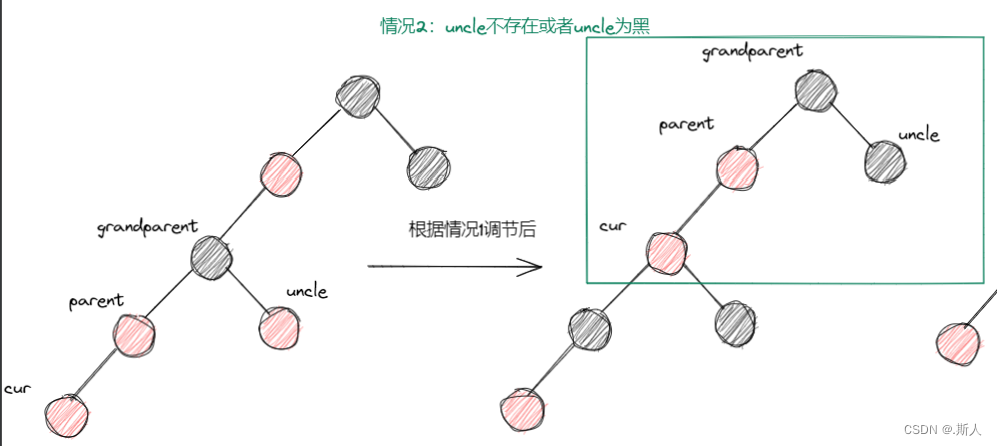
情况2

情况2不会在插入的时候出现，而是在我们向上调节的时候出现

如何处理？

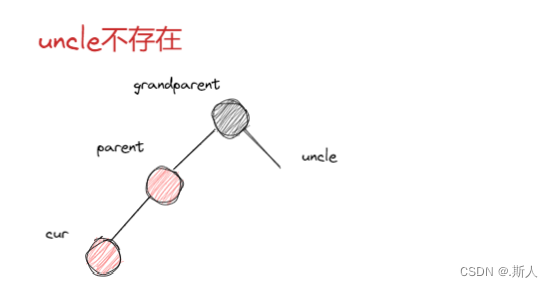
这里考虑的是图二uncle存在的情况，如果uncle不存在，那么代表我们图二的cur必须是新插入的结点，也就是：

核心代码如下
rotateRight(grandparent);//直接调用上一篇AVL文章的右单旋代码即可
parent.rbColor = RBColor.Black;
grandparent.rbColor = RBColor.Red;

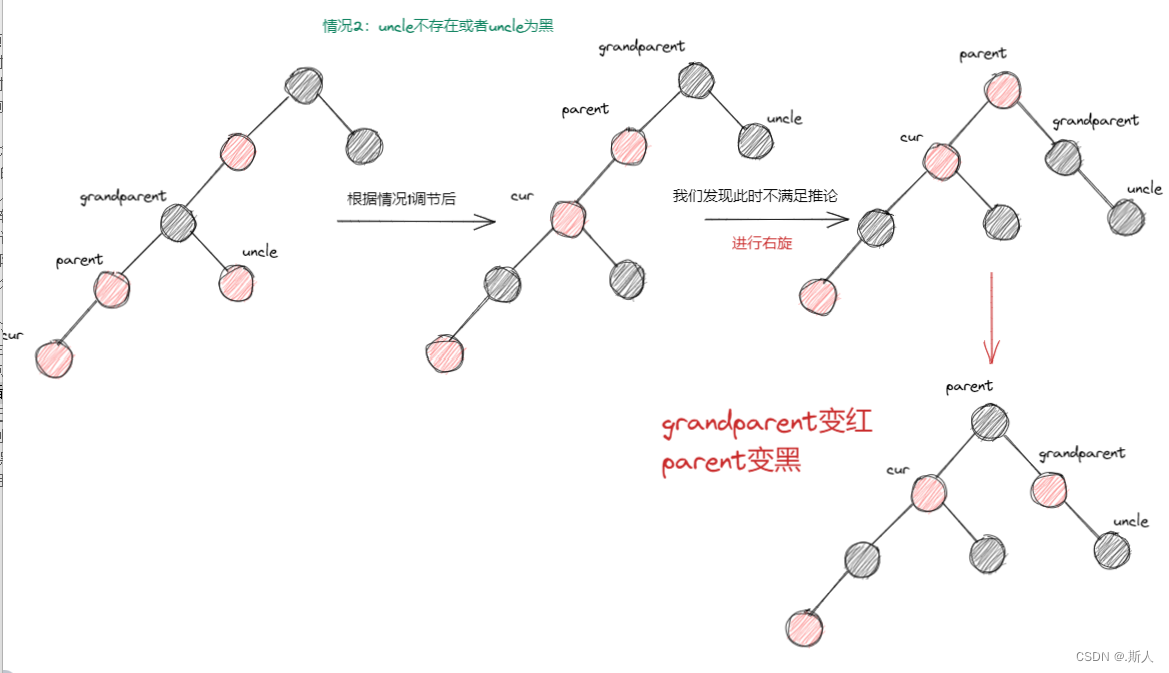
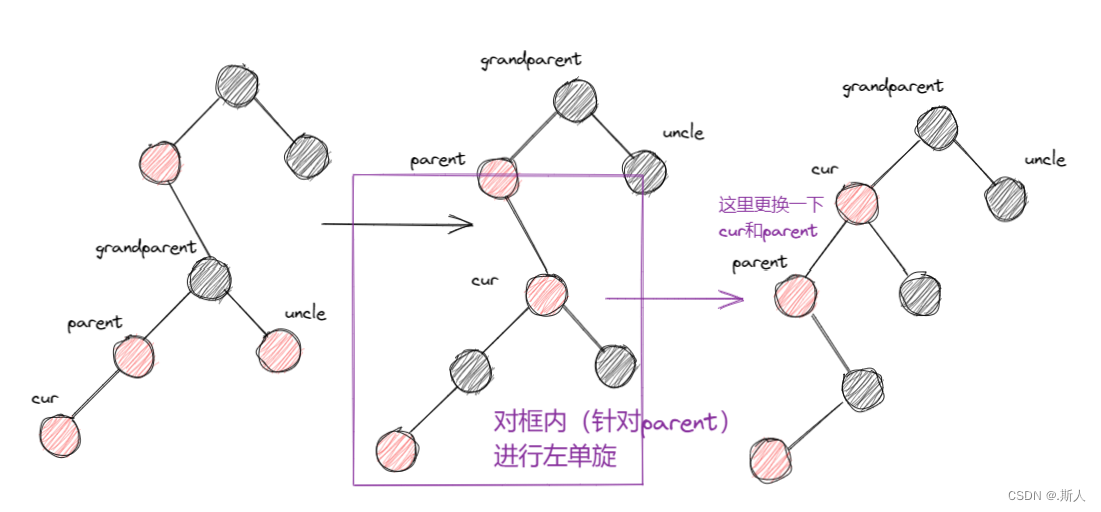
情况3

情况2考虑的是，cur和parent在其父节点同一边的情况，就是cur在parent左边，parent也在grandparent的左边。如果cur在右，parent在左又该如何处理呢？

这里最终的结果上半部分就和情况2的一致了，接下来的调节和情况2也一致

核心代码如下：
if(cur == parent.right){//情况3//先左旋调节为情况2--直接用AVL写过的左旋代码rotateLeft(parent);//调换parent和cur的指向rbNode tmp = cur;cur = parent;parent =tmp;
}

以上都是在

if(parent == grandparent.left){//parent是grandparent的左结点

这个条件下的调节方式，如果

if(parent == grandparent.right){//parent是grandparent的左结点

只要颠倒一下left和right的即可，思路都是一样的。

3.验证红黑树

验证红黑树主要从红黑树的性质来验证

五个性质中，1 2 5都基本上不用验证，主要是验证3 4两个性质和二叉搜索树中序遍历有序。

验证中序遍历有序

遍历即可：

void inorder(rbNode root){if(root == null){return;}inorder(root.left);System.out.print(root.val+" ");inorder(root.right);}

验证性质3

遍历的时候如果当前结点是红色就判断当前结点的父结点是不是红色。

void inorder(rbNode root){if(root == null){return;}inorder(root.left);if(root.rbColor == RBColor.Red){if(root.parent!=null&&root.parent.rbColor == RBColor.Red){System.out.println("结点"+root.val+"的父节点也是红色");}}System.out.print(root.val+" ");inorder(root.right);}

验证性质4

先计算一条路径黑色结点个数，得到结果以这个数为准，判断其他路径是否与之相等

static int blackNum=-1;static int tmpNum=0;static void inorder(rbNode root){if(root == null){//来到了叶子结点if(blackNum==-1){//说明此路径是第一条路径blackNum = tmpNum;}else{//说明此路径不是第一条路径if(blackNum!=tmpNum){//进行验证System.out.println("不满足性质4！");}}return;}if(root.rbColor == RBColor.Red){if(root.parent!=null&&root.parent.rbColor == RBColor.Red){System.out.println("结点"+root.val+"的父节点也是红色");}}else{tmpNum++;}inorder(root.left);System.out.print(root.val+" ");inorder(root.right);if(root.rbColor == RBColor.Black){//代表这个黑色结点不再参与计算，这条路径不走了tmpNum--;}}

验证结果

没有打印其他错误，代码正确！

验证例子：

- 场景1
{16, 3, 7, 11, 9, 26, 18, 14, 15}
- 场景2
{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}

红黑树和AVL树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O( logN)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。

对于这个logN 我作以下解释：

设红黑树有X个黑色结点，总共有N个结点，结点N的范围也就是[X,2X]。

最少：如果这N=X（完全平衡树--和AVL一样），那么时间复杂度就是logX；

最多：如果这N=2X（红黑结点交替），那么时间复杂度就是log2X；

实际上logX和log2X相差并不大，所以就认为两种树的时间复杂度一样。