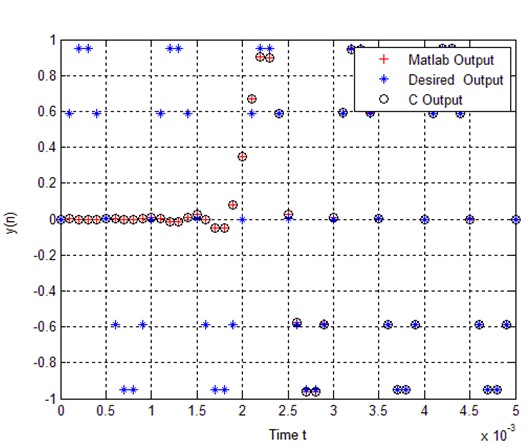
深入理解傅里叶变换的性质:实函数、卷积、相关、功率谱、频响函数
- 1实函数傅里叶变换的性质
- 1.1实函数傅里叶变换的性质
- 1.2实偶函数傅里叶变换的性质
- 1.3实奇函数傅里叶变换的性质
- 2傅里叶变换的基本性质
- 2.1线性
- 2.2对称性
- 2.3折叠性
- 2.4尺度变换性
- 2.5时移性
- 2.6频移性
- 2.7时域微分性
- 2.8频域微分性
- 2.9时域积分性
- 2.10频域积分性
- 2.11时域卷积定理
- 2.12频域卷积定理
- 2.13帕塞瓦尔定理
- 详细的参考资料见:
- 3卷积
- 3.1卷积的定义
- 3.2卷积的计算
- 3.3卷积的性质
- 3.3.1代数性质(乘积类似)
- 3.3.2微积分性质
- 3.3.3卷积的傅里叶变换性质
- 详细参考
- 4相关
- 4.1定义
- 4.1.1相关系数
- 4.1.2协方差函数
- 4.1.3自相关函数
- 4.1.4互相关函数
- 互相关的性质可参考
- 5功率谱与频响函数
- 6卷积与相关的异同(个人体会)
1实函数傅里叶变换的性质
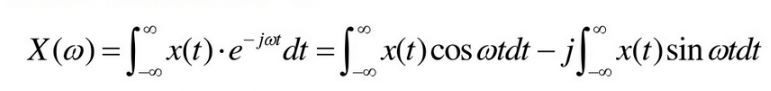
1.1实函数傅里叶变换的性质

所以,实函数x(t)的傅里叶变换X(w)的共轭 X*(w)=X(-w)
1.2实偶函数傅里叶变换的性质

1.3实奇函数傅里叶变换的性质

2傅里叶变换的基本性质
2.1线性
2.2对称性

2.3折叠性
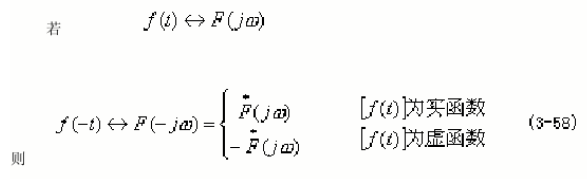
由折叠性和对称性,对实函数f(t),对其傅里叶变换F(jw)的共轭F*(jw)=F(-jw)进行傅里叶变换,再除以2pi,就可得到f(t),也可用傅里叶变换及逆变换公式进行证明。
2.4尺度变换性
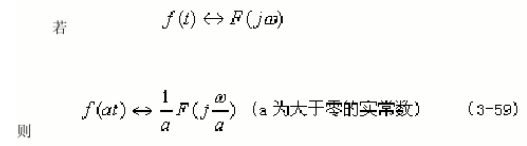
时域信号沿时间轴压缩(或时间尺度扩展)a倍,则其频域信号沿频率轴扩展(或频率尺度压缩)a倍。
改性质反映了信号的持续时间与其占有频带成反比,信号持续时间压缩的倍数恰好等于占有频带的扩展倍数。
2.5时移性
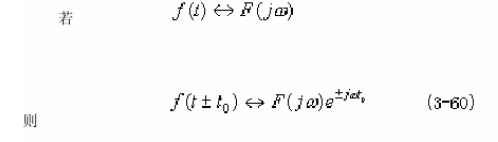
2.6频移性
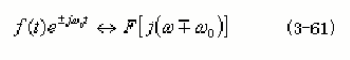
2.7时域微分性
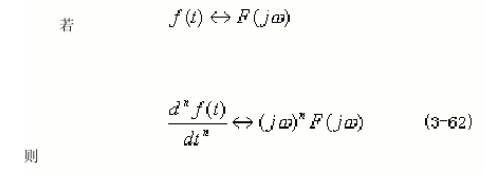
2.8频域微分性

2.9时域积分性
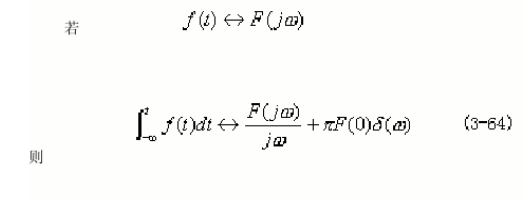
2.10频域积分性
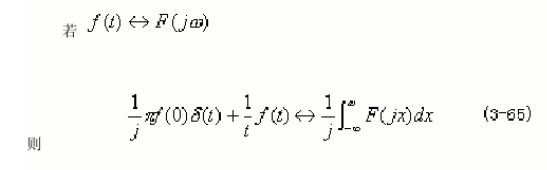
2.11时域卷积定理

2.12频域卷积定理

2.13帕塞瓦尔定理

详细的参考资料见:
链接: https://wenku.baidu.com/view/e581cb01cc17552707220887.html.
3卷积
3.1卷积的定义
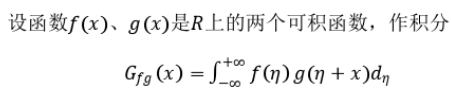
3.2卷积的计算
对折、平移、积分:
3.3卷积的性质
3.3.1代数性质(乘积类似)

3.3.2微积分性质

3.3.3卷积的傅里叶变换性质
见2.11与2.12
详细参考
链接: https://blog.csdn.net/einstellung/article/details/77412903l.
4相关
4.1定义
4.1.1相关系数
相关函数是描述信号X(s),Y(t)(这两个信号可以是随机的,也可以是确定的)在任意两个不同时刻s、t的取值之间的相关程度。两个信号之间的相似性大小用相关系数来衡量。定义:
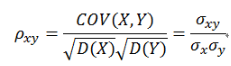
称为变量 X 和 Y 的相关系数。若相关系数 = 0,则称 X与Y 不相关。相关系数越大,相关性越大,但肯定小于或者等于1.。
4.1.2协方差函数
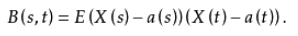
4.1.3自相关函数
自相关函数是信号在时域中特性的平均度量,它用来描述随机信号x(t)在任意两个不同时刻s,t的取值之间的相关程度,其定义式为:
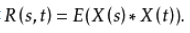
注意:这里*表示相乘。
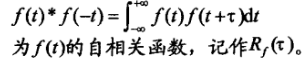
注意:这里*表示卷积。
(1)实函数的自相关函数为偶函数Rxx(-t)=Rxx(t),其图形对称于纵轴,其傅里叶变换=功率谱,为实偶函数,无相位。另外,根据傅里叶变换的定义,可证明Sxx(w)=X(-w)X(w)=X*(w)X(w)=|X(w)|^2。
(2)当s=t 时,自相关函数具有最大值,且等于信号的均方值,即
(3)周期信号的自相关函数仍为同频率的周期信号。
4.1.4互相关函数
互相关函数是描述随机信号X(s),Y(t)在任意两个不同时刻s,t的取值之间的相关程度,其定义为:
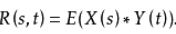
互相关函数的上述性质在工程中具有重要的应用价值。
(1) 在混有周期成分的信号中提取特定的频率成分。
(2) 线性定位和相关测速。
互相关函数的性质
(1)Rxy(t)=Ryx(-t)
(2)对于1、2同周期的函数,相关函数具有相同的周期特性
对信号f(t)g(t),其互相关可定义为:Rfg=f(-t)*g(t)=
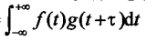
注意??,如果信号是复信号,f(t)要共轭运算后参与运算。
注意有的资料上定义的是- τ \tau τ,与本定义正好相反,值一样,只是时间正负相反。
互相关的性质可参考
链接: https://wenku.baidu.com/view/35136356f011f18583d049649b6648d7c0c7085a.html.
5功率谱与频响函数
功率谱为相关函数的傅里叶变换
Rxx( τ \tau τ)=x(-t)*x(t)=
∫ x ( t ) x ( t + τ ) d t . \int x(t)x(t+\tau)dt\,. ∫x(t)x(t+τ)dt.
Rxy( τ \tau τ)=x(-t)*y(t)=
∫ x ( t ) y ( t + τ ) d t . \int x(t)y(t+\tau)dt\,. ∫x(t)y(t+τ)dt.
上面*表示卷积
对实信号:
Sxx(w)=X(-w)X(w)=X*(w)X(w)
Sxy(w)=X(-w)Y(w)=X*(w)Y(w)
上面*表示共轭
所以频响函数:
H(w)=Sxy/Sxx
H(w)=Syy/Syx
6卷积与相关的异同(个人体会)
卷积与相关都是对函数进行点积,点积在线性空间中表示一个向量向另一个向量的投影,表示两个向量的相似程度,所以相关运算就体现了这种相似程度。
在函数空间中,函数的点积是类似的概念,傅里叶变换的本质是通过对函数与指数函数基(或者三角函数)进行点积计算得到函数在指数函数基下的投影坐标,从而将函数分解成一系列的指数函数分量的。
卷积:f*g( τ \tau τ)=f(t)*g(t)= ∫ f ( t ) g ( τ − t ) d t \int f(t)g(\tau-t)dt\, ∫f(t)g(τ−t)dt=g(t)*f(t)=g*f( τ \tau τ)
卷积满足互换性,这是因为卷积在进行相关的点积计算前,固定f(t),将g(t)反向然后右移动 τ \tau τ,这时,g(t)与f(t)对向而行, τ \tau τ为正的方向;如果固定g(t),f(t)掉头与它对向而行进行点积计算, τ \tau τ为正的方向,计算结果没有不同。
互相关:Rfg( τ \tau τ)= ∫ f ( t ) g ( t + τ ) d t = ∫ f ( t − τ ) g ( t ) d t \int f(t)g(t+\tau)dt\,=\int f(t-\tau)g(t)dt\, ∫f(t)g(t+τ)dt=∫f(t−τ)g(t)dt=Rgf(- τ \tau τ)
互相关不满足互换性,这是因为,互相关计算时,固定f(t),g(t)与它同向而行,t的方向均向右,g(t)左移时 τ \tau τ为正的方向,g(t)时间前移 τ \tau τ与f(t)点积,如果结果较大,说明相关的信号g(t)比f(t)滞后的时间为 τ \tau τ,此时,如果固定g(t)看,f(t)则是向右移动,所以计算结果一样时, τ \tau τ应该为负值。
所以Rfg( τ \tau τ)与Rgf( τ \tau τ)关于0点对称,差别只在于是g(t)滞后 τ \tau τ,还是超前 τ \tau τ。