目录
1 EQ 系数计算和频响曲线绘制
1.1 基本流程
1.2 EQ参数输入
1.3 滤波器系数计算
1.4 频率响应计算
1.5 曲线绘制
2.DRC特性曲线绘制
2.1 基本流程
2.2 参数输入
2.3 增益计算
2.4 静态特性曲线绘制
3 Android 工程实现
1 EQ 系数计算和频响曲线绘制
1.1 基本流程
整个计算和绘制流程如下

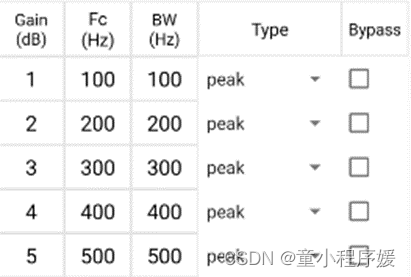
1.2 EQ参数输入
Matlab 和Android两个界面输入如下所示,Android 与Matlab保持一致
| Matlab 界面输入
| Android界面输入
|
1.3 滤波器系数计算
根据输入的EQ参数Gain(dB),Fc(Hz),BW(Hz),Type(滤波器类型:peak、lowshelf、highshelf、lowpass、highpass、bandpass、notch、allpass(0-7)),bypass,以及采样频率fs,可计算滤波器系数sos(b0,b1,b2,a0,a1,a2)。
Matlab 和Java 的调用和实现分别如下图所示
| Matlab 调用 pre_eq_sos = biquad_design(2 * fc / fs, gain, fc ./ bw, type + bypass * 10); (其中fs为采样率) | Java调用 Coeff coeff = BiquadDesign.getSectionsMatrix(gain, fc, bw, type, bypass, fs); |
| Matlab滤波器系数计算实现 function sos = biquad_design(w, g, q, bqtype) %BIQUAD_DESIGN Biquad design. % % INPUTS % % w Normalized frequencies. 0 for DC and 1 for Nyquist frequency. % g Gains in dB at center frequencies % q Quality factors. % bqtype Biquad types. % 0: peak % 1: lowshelf % 2: highshelf % 3: lowpass % 4: highpass % 5: bandpass % 6: notch % 7: allpass % otherwise: bypass % % OUTPUTS % % sos Output filter coefficients in SOS format. validateattributes(w, {'double'}, {'vector', '>=', 0, '<=', 1}) validateattributes(g, {'double'}, {'vector'}) validateattributes(q, {'double'}, {'vector', '>', 0}) validateattributes(bqtype, {'double'}, {'vector'}) if ~isequal(size(w), size(g), size(q), size(bqtype)) error('All input arguments should have same dimensions.') end n = numel(w); sos = zeros(n, 6); for i = 1 : n A = 10 .^ (g(i) / 40); sqrt_A = sqrt(A); sin_w = sin(pi * w(i)); cos_w = cos(pi * w(i)); alpha = sin_w / (2 * q(i)); switch bqtype(i) case 0 % peak b0 = 1 + alpha*A; b1 = -2 * cos_w; b2 = 1 - alpha*A; a0 = 1 + alpha/A; a1 = b1; a2 = 1 - alpha/A; case 1 % lowshelf b0 = A*((A+1) - (A-1)*cos_w + 2*sqrt_A*alpha); b1 = 2*A*((A-1) - (A+1)*cos_w); b2 = A*((A+1) - (A-1)*cos_w - 2*sqrt_A*alpha); a0 = (A+1) + (A-1)*cos_w + 2*sqrt_A*alpha; a1 = -2*((A-1) + (A+1)*cos_w); a2 = (A+1) + (A-1)*cos_w - 2*sqrt_A*alpha; case 2 % highshelf b0 = A*((A+1) + (A-1)*cos_w + 2*sqrt_A*alpha); b1 = -2*A*((A-1) + (A+1)*cos_w); b2 = A*((A+1) + (A-1)*cos_w - 2*sqrt_A*alpha); a0 = (A+1) - (A-1)*cos_w + 2*sqrt_A*alpha; a1 = 2*((A-1) - (A+1)*cos_w); a2 = (A+1) - (A-1)*cos_w - 2*sqrt_A*alpha; case 3 % lowpass b0 = (1 - cos_w) / 2; b1 = 1 - cos_w; b2 = b0; a0 = 1 + alpha; a1 = -2 * cos_w; a2 = 1 - alpha; case 4 % highpass b0 = (1 + cos_w) / 2; b1 = -(1 + cos_w); b2 = b0; a0 = 1 + alpha; a1 = -2 * cos_w; a2 = 1 - alpha; case 5 % bandpass b0 = alpha; b1 = 0; b2 = -alpha; a0 = 1 + alpha; a1 = -2 * cos_w; a2 = 1 - alpha; case 6 % notch b0 = 1; b1 = -2 * cos_w; b2 = 1; a0 = 1 + alpha; a1 = -2 * cos_w; a2 = 1 - alpha; case 7 % allpass b0 = 1 - alpha; b1 = -2 * cos_w; b2 = 1 + alpha; a0 = b2; a1 = b1; a2 = b0; otherwise % bypass b0 = 1; b1 = 0; b2 = 0; a0 = 1; a1 = 0; a2 = 0; end sos(i, 1) = b0 / a0; sos(i, 2) = b1 / a0; sos(i, 3) = b2 / a0; sos(i, 4) = 1; sos(i, 5) = a1 / a0; sos(i, 6) = a2 / a0; end end | Java滤波器系数计算实现 public class BiquadDesign { TYPE_PEAK = 0; TYPE_LOWPASS = 3; TYPE_NOTCH = 6; TYPE_ALLPASS = 7; |
1.4 频率响应计算
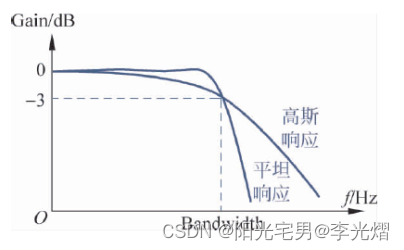
频响是在电子学上用来描述一台仪器对于不同频率的信号的处理能力的差异。同失真一样,这也是一个非常重要的参数指标。频响也称频响曲线,是指增益随频率的变化曲线。任何音响设备或载体(记录声音信号的物体)都有其频响曲线。理想的频响曲线应当是平直的,声音信号通过后不产生失真。
计算数字滤波器的频率响应,根据滤波器系数(传递函数系数),角频率,可返回频率响应向量H。基本计算公式如下所示。

其中b(0),b(1)…b(m),a(0),a(1)…a(n)为滤波器系数,w为角频率。程序的核心就是对该公式的实现。
Matlab 实现
Matlab 通过freqz 函数进行频率响应的计算,主要也是根据上述公式进行计算。其调用方式包括
[H,W] = freqz(SOS,N) returns the N-point complex frequency response
given the second order sections matrix SOS. SOS is a Kx6 matrix, where
the number of sections, K, must be greater than or equal to 2. Each row
of SOS corresponds to the coefficients of a second order filter. From
the transfer function displayed above, the ith row of the SOS matrix
corresponds to [bi(1) bi(2) bi(3) ai(1) ai(2) ai(3)].
[H,W] = freqz(D,N) returns the N-point complex frequency response given
the digital filter, D. You design a digital filter, D, by calling the
designfilt function.
In all cases, the frequency response is evaluated at N points equally
spaced around the upper half of the unit circle. If N isn't specified,
it defaults to 512.
[H,W] = freqz(...,N,'whole') uses N points around the whole unit
circle.
H = freqz(...,W) returns the frequency response at frequencies
designated in vector W, in radians/sample (normally between 0 and pi).
W must be a vector with at least two elements.
[H,F] = freqz(...,N,Fs) and [H,F] = freqz(...,N,'whole',Fs) return
frequency vector F (in Hz), where Fs is the sampling frequency (in Hz).
H = freqz(...,F,Fs) returns the complex frequency response at the
frequencies designated in vector F (in Hz), where Fs is the sampling
frequency (in Hz).
freqz(...) with no output arguments plots the magnitude and
unwrapped phase of the filter in the current figure window.
在本算法中其调用公式如下
f = logspace(log10(20), log10(20e3), 200); //频率20Hz-20kHz 按对数划分为200个点
H = db(abs(freqz(sos, f, fs))); //sos表示2阶截面矩阵,对应滤波器系数[b0,b1,b2,a0,a1,a2],fs为采样频率
Java实现
(1) 根据系数计算某组滤波器下的频响
/* 计算某组滤波器下的频响
*@param coeff 传递函数的系数 b0,b1,b2,a0,a1,a2
* @param w 角频率
* @return 频率响应 (复数类型)
*/
public static Complex getFreqw(Coeff coeff,double w){
Complex complex = new Complex(cos(w),-sin(w)); //欧拉公式e^(-jw)=cos(w)-jsin(w)
Complex b2 = (complex.mul(complex)).mul(coeff.getB2()); //b(2)*e^(-j2w)
Complex b1 = complex.mul(coeff.getB1()); //b(1)*e^(-jw)
Complex hup =b2.add(b1).add(coeff.getB0()); //b(0)+b(1)*e^(-jw)+b(2)*e^(-j2w)
Complex a2 = (complex.mul(complex)).mul(coeff.getA2());
Complex a1 = complex.mul(coeff.getA1());
Complex hdown =a2.add(a1).add(coeff.getA0());
Complex res = hup.div(hdown);
// Log.d("tzw", "getFreqw: "+res.getReal()+"+"+res.getImage()+"i");
return res;
}
注: 欧拉公式e-jw=cos(w)-jsin(w)
(2)多组滤波器下的频响
多组滤波器作用下的频响为各个滤波器频响相乘
/**
* 计算多组滤波器作用下的频响
* @param coeffList 系数组
* @param w 频率
* @return 频响
*/
public static Complex getFreqw(List<Coeff> coeffList,double w){
Complex h = getFreqw(coeffList.get(0),w);
for(int i=1;i<coeffList.size();i++){
h= h.mul(getFreqw(coeffList.get(i),w));
}
return h;
}
(3)幅值、相位计算
之后可根据此计算对应的幅值和相位,如下
/**
* 计算幅值
* @param complex 频率响应
* @return 幅值
*/
public static double getAmplitude(Complex complex){
return Math.sqrt(Math.pow(complex.getReal(),2)+Math.pow(complex.getImage(),2));
}
/**
* 计算相位
* @param complex 频率响应
* @return 相位(-pi/2~pi/2)
*/
public static double getPhase(Complex complex){
return Math.atan(complex.getImage()/complex.getReal());
}
(4)计算一组频率点下的频响幅值(单位:dB),最终调用
/**
* 计算n 个点的频率响应
* @param coeff 系数
* @param fs 采样频率
* @param f 频率数组
* @return n个点的频率响应 (dB)
*/
public static double[] getFreqzn(Coeff coeff,int fs,double[] f){
int n = f.length;
double[] h = new double[n];
for(int i=0;i<n;i++){
double w = 2*Math.PI*(f[i])/fs;
// h[i-1]= getFreqz(coeff,z);
Complex complex = getFreqw(coeff,w);
// h[i-1] = getAmplitude(complex); //幅值
h[i] = 20*Math.log10(abs(getAmplitude(complex))); //分贝(dB)
}
return h;
}
/**
* 计算多个滤波器作用下n个点的频率响应
* @param coeffList 滤波器系数组
* @param fs 采样频率
* @param f 频率数组
* @return n-1个点的频率响应 (dB)
*/
public static double[] getFreqzn(List<Coeff> coeffList,int fs,double[] f){
int n = f.length;
double[] h = new double[n];
for(int i=0;i<n;i++){
double w = 2*Math.PI*(f[i])/fs;;
// h[i-1]= getFreqz(coeff,z);
Complex complex = getFreqw(coeffList,w);
// h[i-1] = getAmplitude(complex); //幅值
h[i] = 20*Math.log10(abs(getAmplitude(complex))); //分贝(dB)
}
return h;
}
1.5 曲线绘制
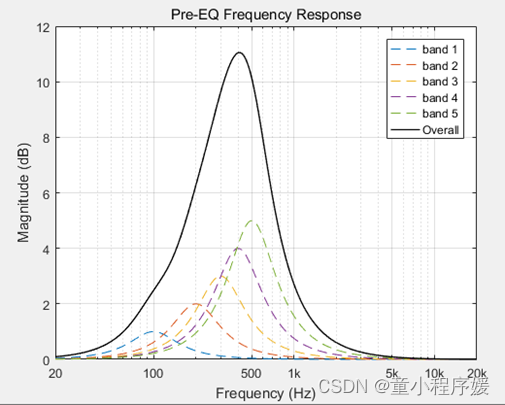
根据2.2界面输入的数据和上述计算,最终进行曲线绘制。Matlab 和Android绘制的曲线如下
| Matlab 绘制
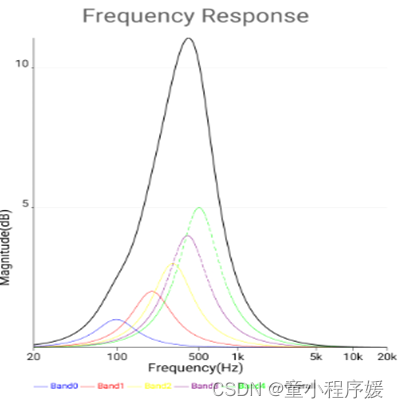
| Android 绘制
|
其中
X轴:频率(Hz):20Hz-20kHz,按照对数划分。
Y轴:频响幅度(dB),彩色线band0-band4表示单个滤波器的频响曲线,黑色线Overall表示所有滤波器作用下的频响曲线。
| Matlab 实现 X轴数据 f = logspace(log10(20), log10(20e3), 200); //频率20Hz-20kHz 按对数划分为200个点 Y轴数据 H = db(abs(freqz(sos, f, fs))); 绘制 (采用半对数绘制) semilogx(f, H1, '--', 'Color', colors(i, :)) semilogx(X,Y)表示半对数绘制,即在 x 轴上使用以 10 为底的对数刻度、在 y 轴上使用线性刻度来绘制 x 和 y 坐标。 最终X轴显示数据:log10(f) Y轴显示数据: H | Android 实现 X轴数据 int n =200; double startF = 20; double endF = 20000; double logStep = (Math.log10(endF)-Math.log10(startF))/n; double[] f = new double[n]; double step = Math.pow(10,logStep); for(int i=0;i<200;i++){ f[i]= startF*Math.pow(step,i); //按对数划分为200个点 } double[] h = FrequencyResponse.getFreqzn(coeff,fs,f); //具体实现见上文Java实现getFreqzn函数 绘制(采用半对数绘制) double[] semilogf = new double[n]; for(int i=0;i<200;i++){ semilogf[i]= Math.log10(f[i]); //半对数绘制时,对f取以10为底的对数 } 最终X轴显示数据:semilogf Y轴显示数据: h |
2.DRC特性曲线绘制
DRC,全名Dynamic Range Control,主要用于调整输入语音的动态范围。应用场景可以有如下的几种形式
(1)类似于AGC的功能,对输入的忽大忽小语音进行动态拉伸,使语音听起来平稳。(2)作为小信号滤除器,滤除低于某一阈值的信号。一般用来滤除噪声,避免噪声在后续模块AGC中被放大。
DRC的原理就是通过设计一条曲线,将输入语音幅度x1通过曲线进行映射得到另一语音幅度值x2。然后计算两者之间的差值得到增益值g,然后根据设置的attacktime和releasetime进行增益平滑以及计算make-up增益,最后再应用到语音得到处理后的语音。
2.1 基本流程

2.2 参数输入
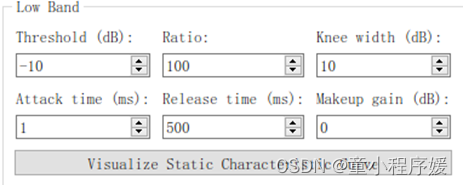
Matlab 和Android两个界面输入如下所示,Android 与Matlab保持一致。主要输入参数Threshold(dB),
Ratio,KneeWidth,Attack time(ms),Release time(ms),Makeup gain(dB)。
| Matlab 界面输入 | Android界面输入
|
2.3 增益计算
增益的计算参考论文“Giannoulis, Dimitrios, Michael Massberg, and Joshua D. Reiss. "Digital dynamic range compressor design - A tutorial and analysis." Journal of the Audio Engineering Society 60.6 (2012): 399-408”
实现代码
| Matlab 实现 function g = compute_gain(u, T, R, W) if nargout > 0 plot(u, u, '--', 'Color', [.8 .8 .8]) function g = compute_gain_core(u, T, R, W) W2 = W / 2; g1 = S * (D + W2).^2 / (2*W); if W | Java实现 /** |
增益计算调用
| Matlab调用 %输入增益 N = 60; u = -N : .1 : 0; %计算y y = u + compute_gain_core(u, T, R, W) %计算Ty Ty = T + compute_gain_core(T, T, R, W) | Java调用 //输入增益 double[] u = new double[601]; //计算y double[] g = CompressorUtil.computeGain(u, t, r, w); //计算Ty double[] tArray = {t}; |
2.4 静态特性曲线绘制
根据上述计算的增益数据u,y,Ty可进行静态特性曲线的绘制,Matlab 和Android绘制的曲线如下
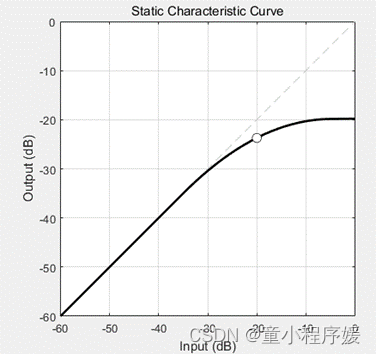
下图中输入数据Threshold(dB):-20,Ratio:100,KneeWidth(dB):30;通过增益计算求得u,y,ty。
| Matlab 绘制
虚线数据:(u,u) 黑色线(特性曲线),数据(u,y), 白色空心拐点,数据(t,ty),t为Threshold | Android 绘制
黄线数据:(u,u) 黑色线(特性曲线),数据(u,y), 红色拐点,数据(t,ty),t为Threshold |
3 Android 工程实现
具体Android工程实现参考:GitHub - tongziwei/EQ: An EQ demo for computing coeffs of transfer function and drawing frequency response characteristic curve.![]() https://github.com/tongziwei/EQ.git
https://github.com/tongziwei/EQ.git
工程主界面

EQ1 频响曲线绘制
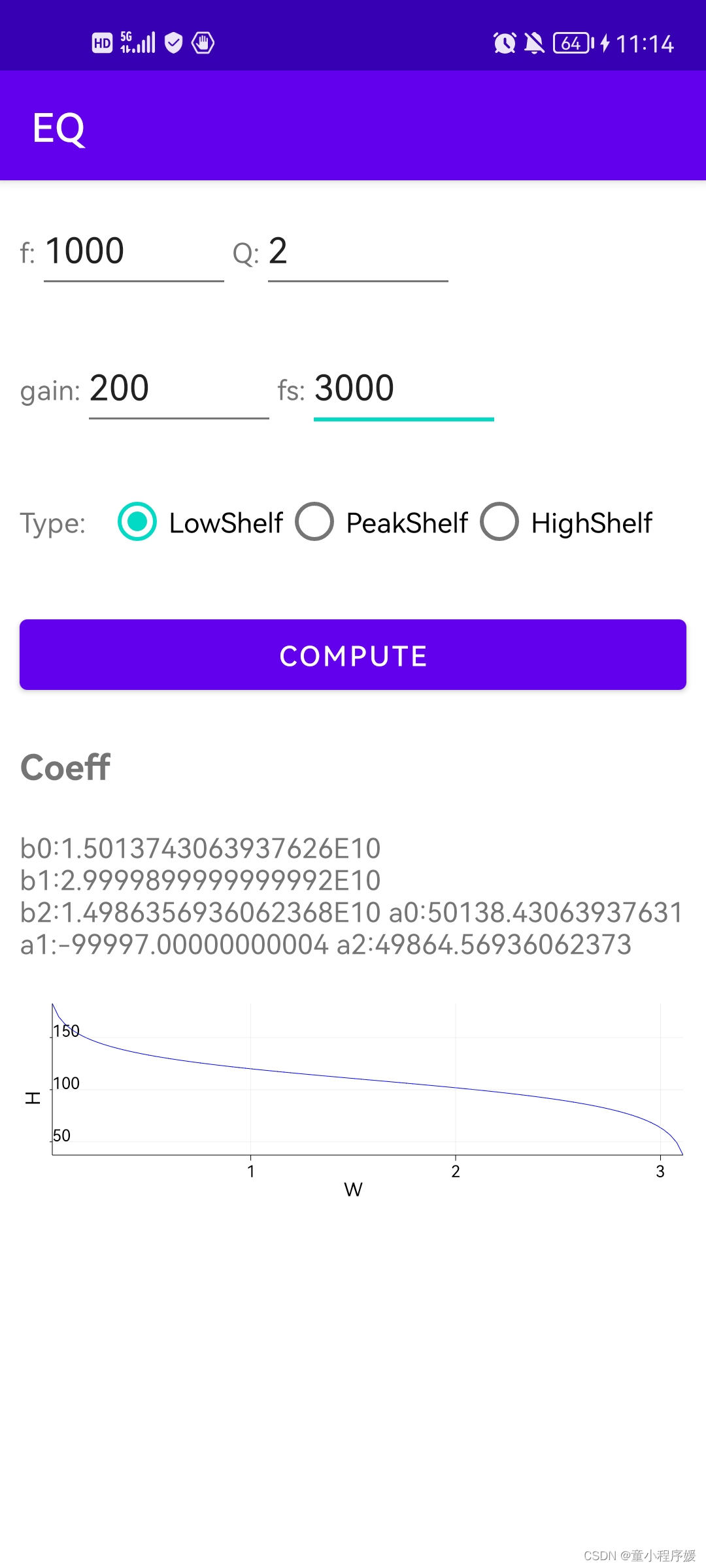
可通过直接输入f,Q,Gain,fs,选择滤波器类型(三种滤波器LowShelf,PeakShelf,HighShelf)计算对应的滤波器系数,并绘制频响曲线图。
EQ2 频响曲线绘制
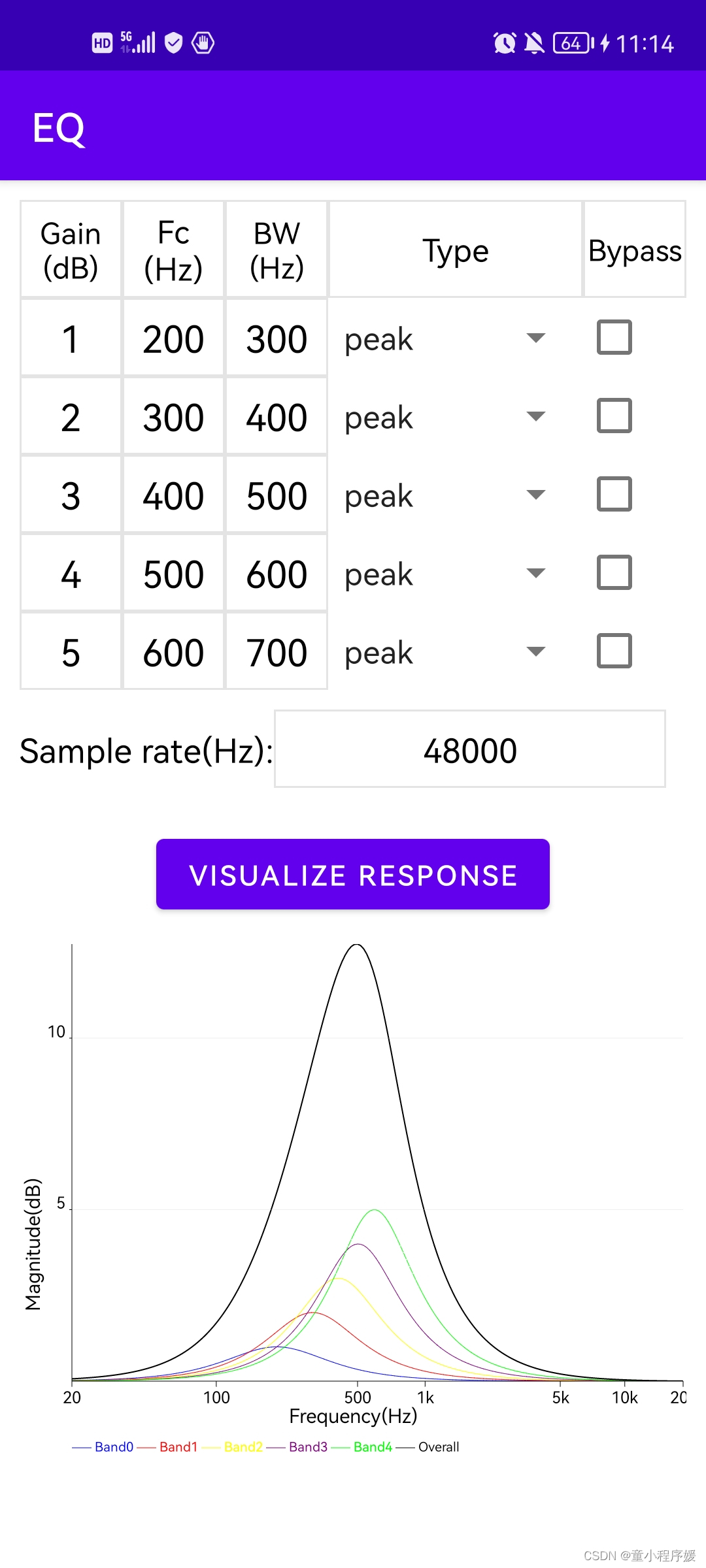

可通过直接输入Gain,fc,Bw, 采样率fs,选择滤波器类型(8种滤波器LowShelf,PeakShelf,HighShelf)计算对应的滤波器系数,并绘制频响曲线图。具体实现参考上文EQ系数计算和频响曲线绘制。
DRC特性曲线绘制
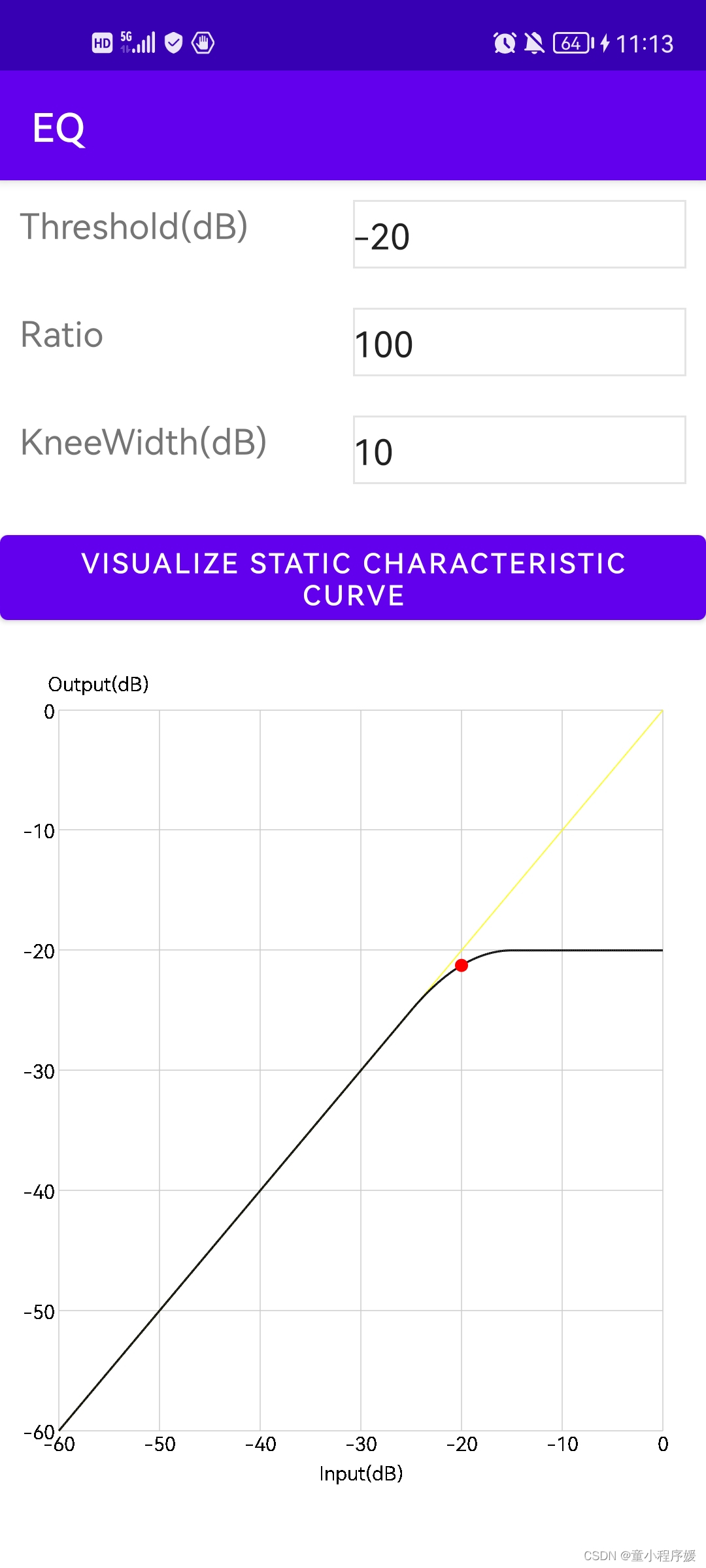
通过输入Threshold,Ratio,KneeWidth,计算增益,绘制特性曲线图,具体实现参考上文DRC特性曲线绘制。