汽车的四自由度振动模型

m：车身的等效质量；
m_1：前轴的等效质量(包含电机的质量在内)；
m_2：后轴的等效质量；
m_3：人体和座椅的等效质量；
x_0：车身的重心在铅垂方向的位移；
x_1：前轴非悬挂质量在铅垂方向的位移；
x_2：后轴非悬挂质量在铅垂方向的位移；
x_3：人体和座椅在铅垂方向的位移；
k_1：前悬架的刚度系数；
k_2：后悬架的刚度系数；
k_3：座椅的刚度系数；
k_4：前轮刚度系数；
k_5：后轮刚度系数；
c_1：前悬架减振器的阻尼系数；
c_2：后悬架减振器的阻尼系数；
c_3：座椅的阻尼系数；
F(t)：电机的激励。

频响函数法

频响函数是自动控制理论中描述系统输出和输入之间函数关系的一个非常重要的物理量，只与系统本身的特性参数有关，与激励力的类型和大小无关，不同类型激励力作用下的表达形式不同。

工程振动领域一般也将其称为机械导纳，在振动分析和测试技术领域有着极为广泛的应用，也是模态参数辨识和载荷识别技术中常用的物理量。对系统进行频响特性分析可以了解系统的幅频和相频等内在属性，当给定激励时，还可以利用频响函数进行系统响应的快速求解，求解过程如下：

根据牛顿第二定律，建立系统的作用力方程如下：

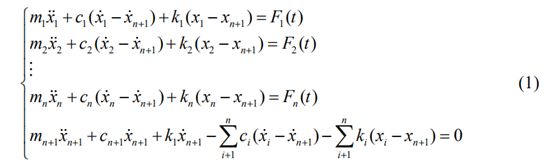
写成矩阵形式：

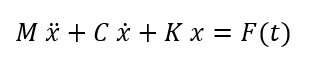
上式中各矩阵和列向量分别为：

建立系统的运动微分方程如下：

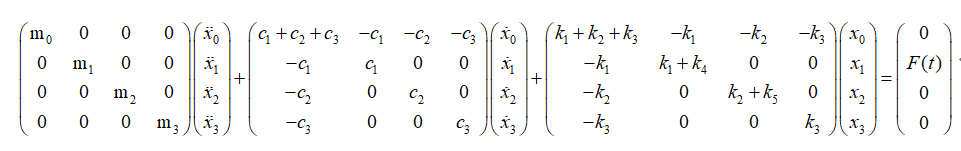
系统的频响函数矩阵为：

根据上式，可以很容易根据线性代数的知识得到具体表达式，由于表达式过于复杂，要想查看具体结果可以运行代码查看结果。

系统的稳态响应为：

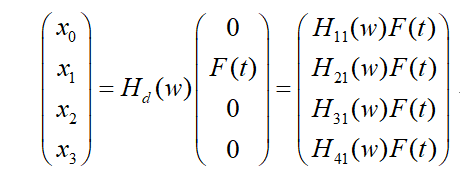
运行MATLAB程序得到：

频响函数法和机械阻抗法相比各有特点，频响函数法的响应求解在多激励情形的速度更快，但与经典牛顿力学体系或分析力学体系的分析方法（如马上要介绍的模态分析方法）一样需要知道系统的运动方程；而机械阻抗法不需要建立系统的运动微分方程，但是需要画出系统的机械网络图，尤其是对多激励的响应求解需要根据叠加原理，这样求解速度会大受影响。

MATLAB程序

% 此程序是用频响函数法求系统稳态响应
clc;
clear;w = 2*pi;
m = 1354.5;
m1 = 80;
m2 = 68.5;
m3 = 102;
c1 = 600;
c2 = 550;
c3 = 400;
k1 = 18000;
k2 = 16997;
k3 = 5200;
k4 = 118000;
k5 = 118000;
j = sqrt(-1);
t = 0:0.2:20;
F = 20*exp(w*t*j);% 质量M矩阵
M = [m 0 0 0;0 m1 0 0;0 0 m2 0;0 0 0 m3];
% 阻尼系数C矩阵
C = [c1+c2+c3 -c1 -c2 -c3;-c1 c1 0 0;-c2 0 c2 0;-c3 0 0 c3];
% 弹簧系数K矩阵
K = [k1+k2+k3 -k1 -k2 -k3;-k1 k1+k4 0 0;-k2 0 k2+k5 0;-k3 0 0 k3];
%求解传递矩阵
Hd = inv(K - M*w*w + j*w*C);
%X = Hd * F;
x0 = Hd(1,1)*F;
x1 = Hd(2,1)*F;
x2 = Hd(3,1)*F;
x3 = Hd(4,1)*F;
figure()
subplot(2,2,1)
plot(t,x0)
title("激励x0")
xlabel("t(s)")
ylabel("位移/m")
subplot(2,2,2)
plot(t,x1)
title("激励x1")
xlabel("t(s)")
ylabel("位移/m")
subplot(2,2,3)
plot(t,x2)
title("激励x2")
xlabel("t(s)")
ylabel("位移/m")
subplot(2,2,4)
plot(t,x3)
title("激励x3")
xlabel("t(s)")
ylabel("位移/m")