6.1 概述

1. 关心稳态响应，令拉氏变换的s=jw，实现从复频域到频域的转换。
2. 频率响应的实际求解：代入电阻、电容的复频率阻抗，。模拟电路（低频）一般不考虑电感sL。相频特性：时域上反映输出对输入的延迟Δt，Δφ=(Δt/T)×2Π，高频时延迟对相位的影响很大。
3. 两极点系统的幅频响应=两个单极点系统的幅频响应之积；相频响应=两个单极点系统的相频响应之和。
4. 如果，则称为主极点，主极点对频率响应的影响（衰减幅值、相角phase angle移动）更大。
   
   极点在左半平面（LHP）时，输出信号的相位比输入滞后。极点在右半平面（RHP）时，输出信号的相位比输入超前。
   右半平面的零点（RHZ）和LHP的作用相反。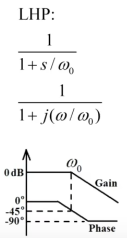
   
   
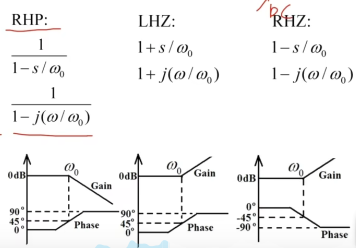
   衰减速度：-20dB/dec（频率增加到10倍时，增益下降了20dB），-40dB/dec...
   传输函数的magnitude，当频率通过zero frequencey时以+20dB/decade、+40dB/dec上升。 “-3dB带宽”“cutoff frequency”
   处相位变化了±45deg、处±135deg...
    
5. 频率特性：电压源+串联RC=电流源+并联RC
   
    
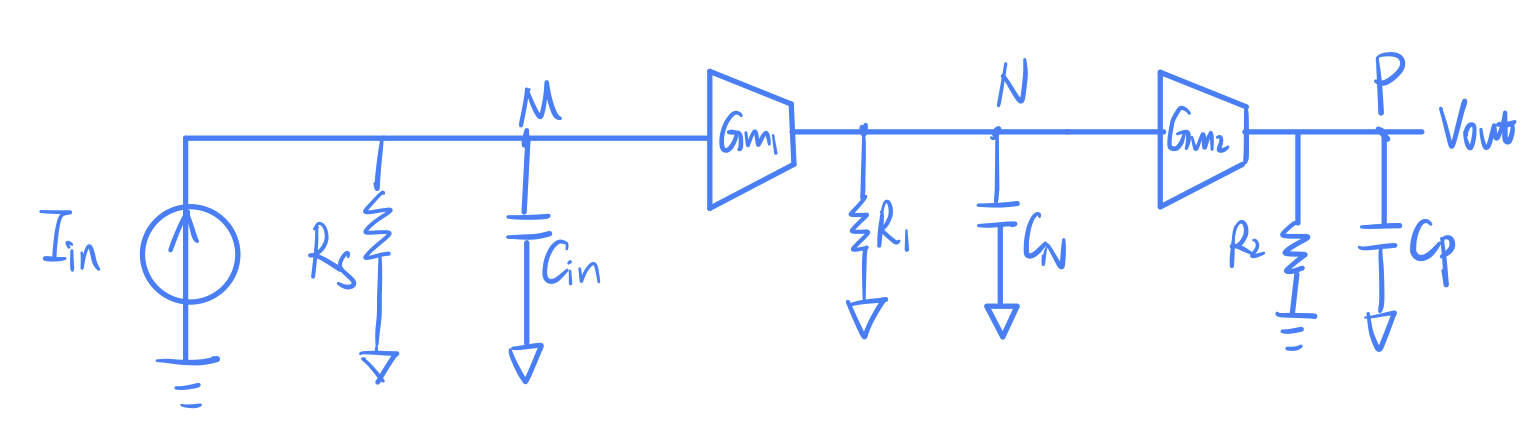
6. 电路的每个node贡献一个pole。可以采用结点分析法直接写出传递函数：pole=从结点看向地的电阻×对地的总电容。复杂情况：feedback branch 在结点之间产生联系。
    
7. Miller’s theorem--decomposition of a "floating" impedance into two "grounded" impedances
   Miller’s approximation：用低频时的增益分析高频。缺点：可能消除了传递函数的zeros、预测额外的poles、不能正确计算输出阻抗。
   
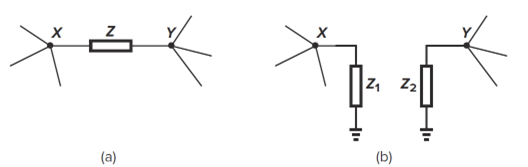
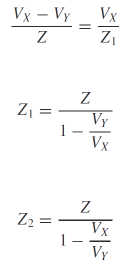
   注：如果Z在X和Y之间只有一个信号通路，则密勒定理不适用。
   典型案例：和增益为的放大器主通路并联。
   通常用的直流增益来分解
   
   应用：实现电容放大，节省芯片面积。缺点：对放大器的输出摆幅要求高；更大的功耗。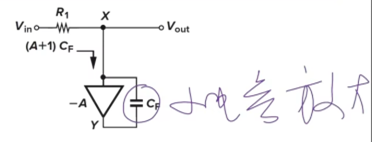
   
   
    
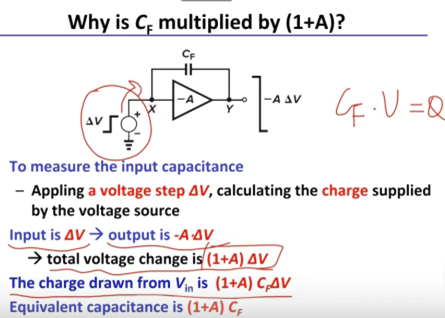
8. transit frequency：器件的小信号电流增益为1时的频率。

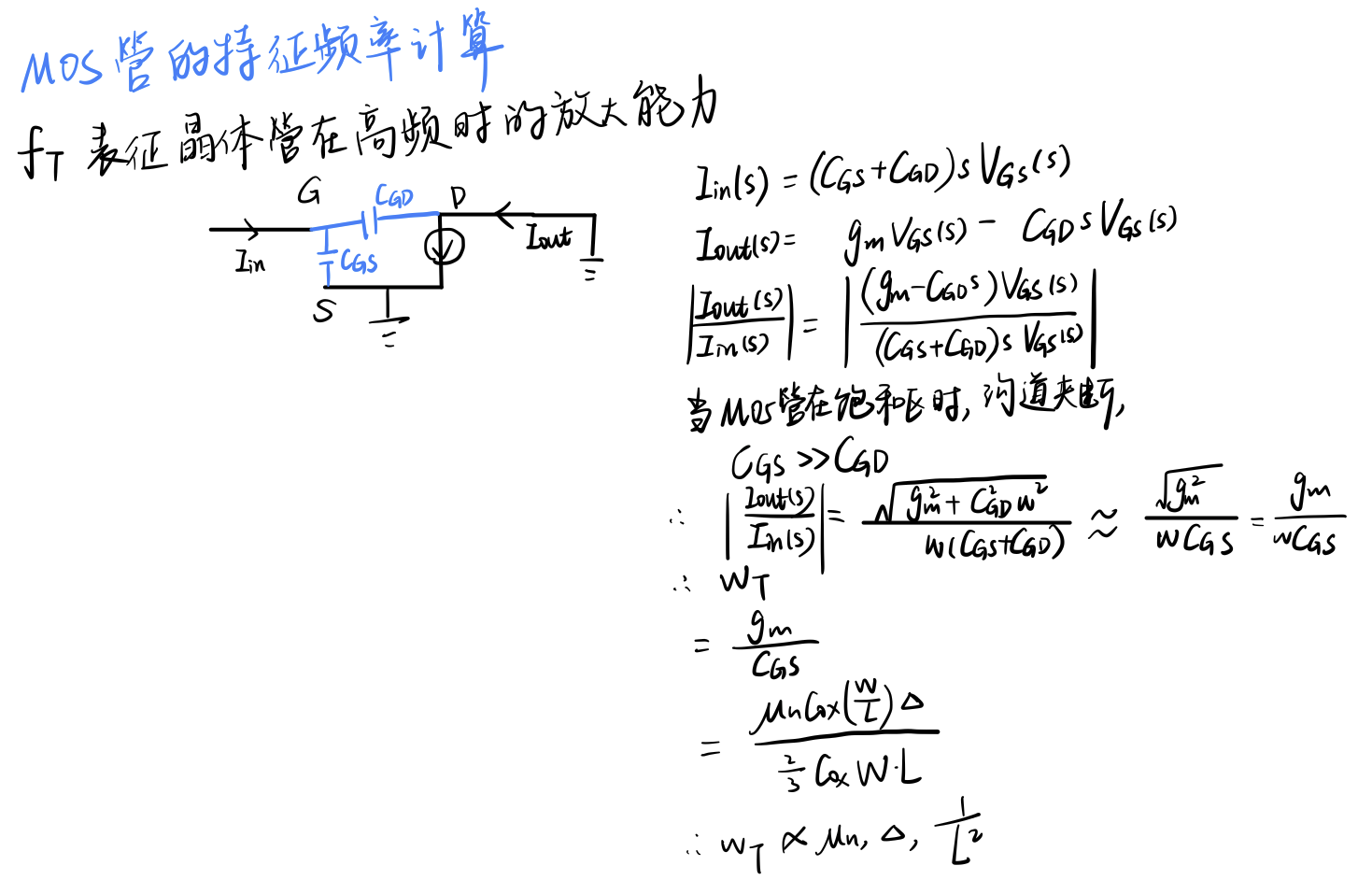
   随着过驱动电压增加到一定程度，由于速度饱和，会导致迁移率明显逐渐减小，而使ft-Vod曲线变平,不再是线性直线。
   

---

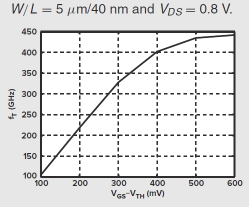
6.2 共源极

方法1：通过密勒近似，直接求出极点频率

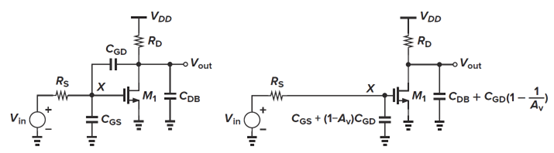
1. 误差1：忽略了输入输出（通过）耦合产生的零点。
   
2. 误差2：放大器的增益会随频率变化。当电路驱动大的负载电容时，低频时的电压增益会下降，此时不能用低频增益计算密勒效应的乘积项。
    

方法2：利用小信号电路，直接推出传递函数，然后利用 主极点近似 反推极点和零点。

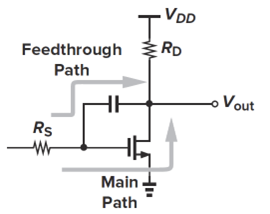
1. 零点频率：，比特征频率大。是RHZ，增加了输出相移，损害电路的稳定性。零点产生的原因：两条以上的path。除了主通路，提供了前馈feedforward通路。
    
2. 一种简单的计算零点的方法：令输出电流为0。根据KCL定律有
   [ 极点：传递函数输入为0时，输出不为0。零点：传递函数输入不为0时，输出为0。
   "We have seen that the signals traveling through two paths within an amplifier may cancel each other at one frequency, creating a zero in the transfer function." ]
    
3. CS输入容性阻抗（resistance是impededance的实部）：高频时，存在输入电流。前馈影响了输入阻抗，不再是单纯的容抗，而是复阻抗。

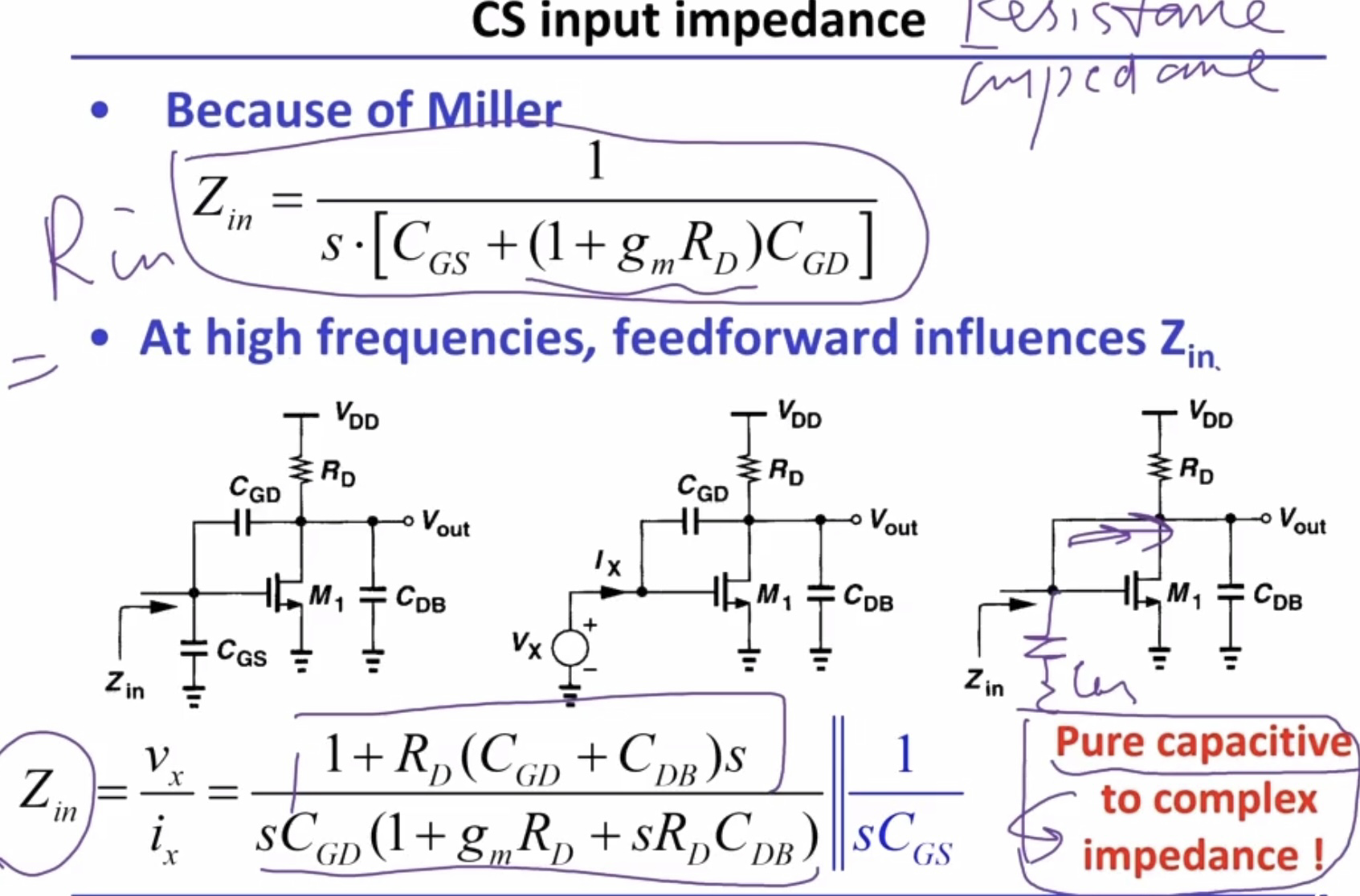
Class-AB stage：和CS级结构相同。等效小信号模型：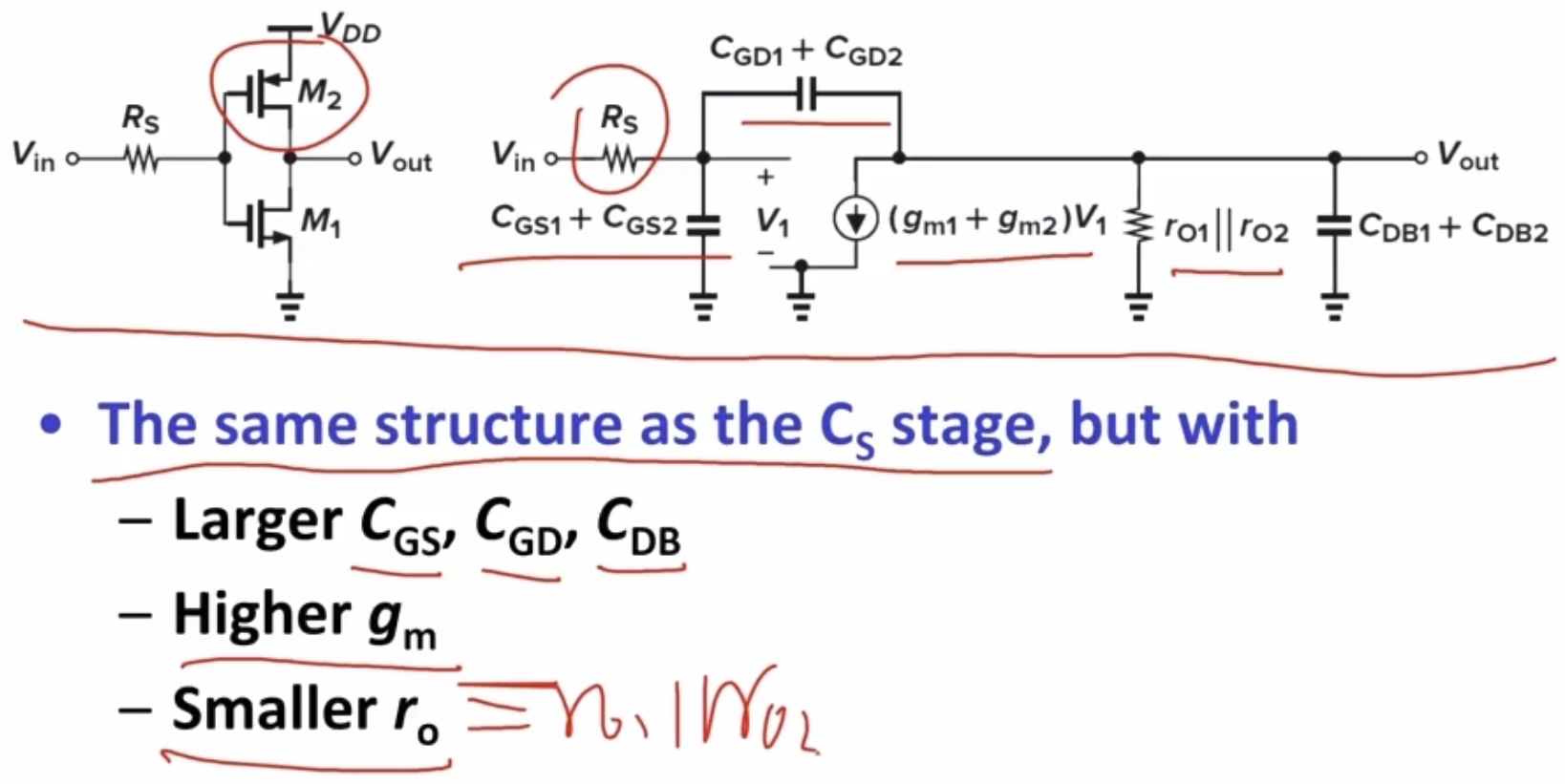

---

6.3 源跟随器

1. 传输函数包含一个在左半平面的零点。原因：高频时，由传导的信号与本征晶体管产生的信号以相同的极性相加。
2. 当为0，且不考虑沟调效应和体效应的情况下， is bootstrapped，没有电流通过，不贡献零极点。
3. 高频时，驱动负载电容的源跟随器会显示出负的输入电阻，可能引起不稳定。负阻特性可被用于振荡器oscillator。
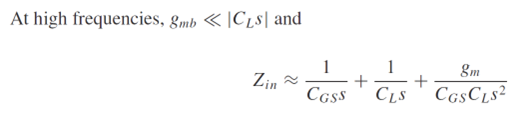
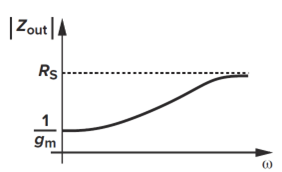
4. 若源跟随器前一级输出阻抗很大，则源跟随器的输出阻抗表现出电感特性（随频率增加）
   

---

6.4 共栅级

1. 如果不考虑沟调效应，输入、输出结点是isolated。如果不忽略，输入阻抗和负载阻抗、有关。
2. 如果与栅串联的是大阻抗，则降低了极点频率。