源自:系统公正与电子技术
作者:李梦杰 常雪凝 石建迈 陈超 黄金才 刘忠
摘 要
武器目标分配问题是指挥控制与任务规划领域的关键难点之一, 也是军事运筹领域的基础研究课题。经过多年研究, 武器目标分配问题在陆海空天电等领域都得到了广泛研究, 涌现出了大量模型和算法。系统梳理武器目标分配问题的典型作战样式、建模方法、求解算法和实验验证, 掌握当前该领域的研究现状, 在此基础上, 结合智能化、无人化战争带来的新挑战, 分析武器目标分配的发展趋势, 为后续研究提供参考。
关键词
武器目标分配 ; 模型 ; 算法 ; 综述
引 言
武器目标分配(weapon target assignment, WTA)问题是军事运筹学领域的基础问题之一, 是解决如何将多种作战武器分配给多个打击目标, 来最优地实现指挥员的作战意图, 也是指挥控制自动化、智能化需要解决的关键问题。
WTA问题最早由Manne(1958)[1]在研究弹道导弹防御运筹优化时提出, 开始被称为导弹分配问题(missile allocation problem, MAP), 解决如何将己方拦截导弹分配到来袭弹道导弹的拦截作战中, 以达到己方设施最优防护的目的。该问题提出后, 受到军方和学术界作战运筹、指挥控制、自动化等领域研究人员的广泛关注, 开始逐步将MAP的基础模型扩展到不同的作战领域, 成为当前熟知的WTA问题。WTA问题是典型的组合优化问题, 随着武器、目标的种类和数量的增加, 解的数量会呈指数增加。20世纪80年代, Lloyd等(1986)[2]证明了WTA是一个多参数、多约束的NP(non-deterministic polynomial)-complete问题。曹奇英等(2001)[3]说明了WTA问题的解空间存在大量的局部极值点, 往往是不可微的、不连续的、有约束条件和高度非线性的。因此, 不存在确定性优化算法能在多项式时间之内计算出问题最优分配方案。
从作战指挥决策过程来看, 当前常见WTA问题研究主要分为两大类: 静态WTA(static WTA, SWTA)和动态WTA(dynamic WTA, DWTA)。SWTA问题研究一个确定的周期内, 己方武器对敌方目标进行一个回合交战的最优分配。DWTA问题在SWTA的基础上引入时间维的决策, 在多个回合的交战中考虑己方武器和敌方目标在类型、数量和状态等方面的不确定性, 为目标的动态打击提供武器筹划方案。此外, 多阶段WTA问题研究己方武器分多个阶段(波次)对敌方目标进行打击, 优化确定条件下多阶段交战过程中武器资源的筹划方案, 属于一类较为特殊的WTA问题, 有时被归入到DWTA问题中。从决策权来看, 可以分为集中WTA和分布式WTA。
WTA问题经过几十年的研究, 在模型、算法、作战应用以及实验数据等方面都得到了巨大发展。从建模方法来看, 早期以整数规划、动态规划和图论等方法为主, 近期博弈论、多智能体方法等也开始用来对WTA问题进行建模求解。从优化算法来看, 既有传统的分支定界法、割平面法和列生成方法等传统精确算法, 也有贪婪搜索、禁忌搜索(tabu search,TS)算法、模拟退火(simulated annealing,SA)算法、大规模邻域搜索(very large-scale neighborhood search,VLNS)算法、粒子群优化(particle swarm optimization,PSO)算法、遗传算法(genetic algorithm,GA)、蚁群优化(ant colony optimization,ACO)算法等启发式算法,以及多种启发式算法结合的混合智能算法等。从应用领域的作战样式来看, 包括了防御过程中的地面防空、空中拦截、单舰防空、舰艇编队防空、反弹道导弹等, 以及进攻过程中的地对地打击、空对地打击、反舰、装甲对战、联合火力打击等在内的10多种典型作战样式。从模型算法的实验验证来看, 既有10种以内武器和目标的小规模算例, 也有数量高达400种武器和目标的大规模算例。
Matlin(1970)[4]对20世纪70年代之前的(导弹)WTA问题的相关研究进行梳理和分析, 侧重静态模型和启发式算法的总结。Cai等(2006)[5]对20世纪初及之前的WTA研究进行了综述, 更加着眼于DWTA的研究进展和发展趋势。Kline等(2019)[6]的研究是近期WTA问题领域较为全面的综述, 重点对WTA的数学规划模型和算法进行了总结。上述综述主要关注英文论文中的研究成果, 还缺少国内代表性成果的总结。同时, 对具体模型和算法总结较多, 没有系统总结WTA的应用场景和实验数据。
随着人工智能技术、无人系统等新技术新装备在军事领域的广泛应用, WTA问题也面临着新的挑战与发展机遇。无人系统的应用催生了很多新的作战样式, 如蜂群作战、跨域无人集群协同作战等。如何在现有WTA研究的基础上, 研究新作战样式下的WTA技术, 将是未来智能化、无人化作战领域的一个研究热点。同时, 人工智能技术为更高效地解决动态对抗场景下的WTA问题提供了新的解决思路。因此, 从典型应用场景、建模方法、算法以及实验等多个角度对WTA问题进行系统综述, 同时融入了国内的代表性研究成果, 文献更加全面, 内容更加丰富, 为下一步WTA的新发展奠定基础, 具有重要的应用价值。
1 典型作战样式
WTA问题在典型的防御和进攻作战中都有着十分广泛的应用, 在地面防空、舰艇防空、空中拦截、协同空战等典型防御作战样式以及地对地打击、空对地打击、反舰、装甲对战、联合火力打击等典型进攻作战样式中支撑指挥员快速制定WTA方案。从作战领域来看, WTA在陆海空天等领域的作战规划中都发挥着重要作用, 电磁领域一般为作为外部约束或影响, 融合到其他领域的典型WTA中。其中, 海上作战中的海空一体化作战既属于典型的联合作战, 又包含了舰艇防空、反舰、(舰载机)空对地打击、协同空战、联合火力(舰载导弹、远程火炮等)打击等典型防御与进攻作战样式。本文重点从进攻和防御作战的角度进行了分析总结。典型作战样式如图 1所示。

1.1 防御作战
未来战争的主要形式是非接触作战, 防御作战是防御敌方攻击或者破坏敌方攻击武器, 使敌方攻击性武器失去威胁, 以最大效用保护己方安全。当今世界的主题仍然是和平与发展, 在WTA的研究应用中, 防御作战是重要的应用方向。
1.1.1 地面防空
地面防空是指拦截敌方空中来袭目标以保护己方资产, 最主要的拦截目标是巡航导弹、弹道导弹、火箭弹以及敌方各型飞机等。己方的资产主要包括城市、机场、港口以及其他重要设施, 防御的主要目标是最大化摧毁敌方来袭目标或者最大化保护我方资产。
自Manne(1958)[1]提出WTA问题以来, 相关的MAP研究一直延续至今, Matlin(1970)[4]对1970年之前的MAP文献进行了分类梳理。Soland(1973)[7]研究了区域防御和点防御中反弹道导弹的WTA问题。Wacholder(1989)[8]分析了洲际弹道导弹防御中的WTA问题, 以来袭目标剩余威胁最小化为目标, 同时考虑了每个防御平台所拥有拦截武器的上限以及分配给一个目标的拦截武器上限。Bertsekas等(2000)[9]同样研究了战区导弹防御的WTA问题, 不同的是, 其研究的是更为复杂的动态导弹防御问题, 同时考虑了来袭目标的多样性、己方资产价值的大小和防御武器的有限性, 以最后阶段己方资产保存价值最大化为优化目标。
刘付显等(2003)[10]基于地空导弹防御系统多目标通道数的不同杀伤区, 研究了最大化拦截敌方武器的WTA问题, 考虑了时间约束、空间约束和资源约束。Menq等(2007)[11]分析了多层弹道导弹防御系统的WTA问题。Wang等(2011)[12]主要研究了地空导弹战术单元防空指挥控制系统中的目标分配问题, 提出了火力单元拦截目标的射击优势度概念。Wang等(2015)[13]研究了一般弹道导弹防御的WTA问题。Severson等(2015)[14]重点研究了雷达资源对来袭的弹道导弹和巡航导弹的分配问题, 雷达在作战中扮演着搜寻、追踪和制导等角色, 雷达资源分配起着重要作用。
Li等(2016)[15]研究了多层多波次来袭弹道导弹拦截的WTA问题, 多层主要是指高空防御层和低空防御层, 防御方根据不同的防御层发射不同的拦截器, 在分配拦截器时考虑了时间窗口。Davis等(2017)[16]和Xu等(2017)[17]都研究了弹道导弹防御WTA问题。前者基于动态的角度研究了不确定性的多轮次齐射的弹道导弹防御问题, 出发点是最大化保护己方资产(例如城市); 后者基于静态的角度研究了不确定条件下的多目标WTA问题, 以获得最大的拦截效率和最小的拦截损耗。Li等(2018)[18]研究了静态多目标地面防空的WTA问题, 在最大程度保护己方资产的同时最小化武器消耗。欧阳志宏等(2018)[19]从软杀伤角度研究了电子干扰对抗来袭威胁的目标分配问题, 通过干扰来袭目标的激光、电视、红外等制导方式, 优化己方电子武器配置达到最佳电子干扰效果。
Jang等(2019)[20]重点研究了高命中概率的拦截器拦截敌方导弹的WTA问题。Guo等(2019)[21]主要研究具有固定和自适应分组约束的多对多导弹拦截问题, 分组策略主要考虑了对每个目标分配武器的数量限制。Xu等(2020)[22]主要研究了双目标多阶段防空WTA问题, 重点突出了传感器平台和武器平台的合作, 以最后阶段拦截的所有来袭目标威胁最大化和总成本最小化为优化目标。Zhang等(2020)[23]通过提炼典型地空反突防场景的关键因素, 提出了一个动态传感器/异构武器-目标集成分配问题, 即目标由远及近的突防过程中, 调配近、中、远多类型防御武器以及传感器对目标进行拦截。
1.1.2 舰艇防空
舰艇编队作战是现代海战的重要作战方式, 有其显著特点, 舰艇防空通常是多波次防御, 特别是在海上对抗中节奏快, 时间反应要求非常高。舰艇防空主要是指舰艇防御敌方空中威胁, 敌方威胁主要包括战斗机、反舰导弹等, 己方防空武器主要包括搜索雷达、电磁信号监视器、火控系统以及导弹、火炮、电子干扰、诱饵弹等, 防空的主要目的是保护己方安全, 最大化摧毁敌方来袭目标。舰艇防空又可分为单舰防空和舰艇编队防空。舰艇防空作战节奏快, 因此WTA的时效性要求高, 一般以构造式启发算法为主, 在极短时间内快速生成防空武器分配方案。
(1) 单舰防空
Lee等(1994)[24]研究了单艘舰艇执行区域防空的WTA问题。Van等(1995)[25]研究了海军护卫舰的防空战斗力的快速评估问题, 辅助决策者快速比较不同策略、系统和冲突之下方案的优劣。张勇等(2005)[26]分析了舰艇防空武器系统多通道的特点, 根据各射击通道的转火能力和射击时间, 建立了最大化拦截来袭导弹的WTA模型。罗江锋等(2013)[27]以加拿大Halifax级护卫舰为例将智能规划与优化调度的方法应用于舰艇防空武器规划中, 利用智能规划快速搜索出可能的备选方案, 再利用优化调度的方法产生最优的WTA方案。
(2) 舰艇编队防空
Li等(2006)[28]研究了舰艇编队的DWTA问题, 在舰艇编队防空作战中, 优化目标是使在防空作战最后阶段幸存的目标总威胁最小。Karasakal(2008)[29]针对海军任务组的防空WTA问题进行了研究, 强调舰艇编队的相互配合, 考虑了不同舰艇的重要性以及舰艇之间的相互防御, 将击落所有来袭导弹的概率最大化作为优化目标。王玮等(2008)[30]分析了舰艇编队WTA的模式, 研究了舰艇编队集中式指挥和分布式指挥的WTA方法。韩双等(2009)[31]研究了舰艇编队防御问题, 提出先对来袭目标的威胁做出排序并产生一个初步的WTA方案, 然后再送往融合中心借助大系统理论的分解协调法进行优化。
王玮等(2009)[32]、李相民等(2010)[33]、陈华东等(2010)[34]研究了基于多智能体的舰艇编队WTA问题。李亦伟等(2010)[35]分析了舰艇编队防空武器之间的软硬火力的配合。陈华东等(2013)[36]将舰艇编队的武器目标系统看作一个多智能体系统, 并基于黄页服务中的合同网协议生成编队武器分配方案。
Karasakal等(2011)[37]主要研究了舰艇编队的MAP, 这种分配问题是以防御性为主即舰载防空导弹拦截反舰导弹, 考虑了多种导弹系统和反舰导弹类型, 并根据交战过程中的射击-观察-射击策略, 建立了一个离散模型辅助生成舰艇编队最佳参与时刻表。同年, Karasakal等[38]研究了舰艇编队的最佳防御阵型问题, 以确定舰艇的位置和扇形防御区, 从而形成最佳的防御网络。
Chen等(2012)[39]在研究舰艇编队防空问题中考虑了舰艇编队主舰或者指挥舰的重要性, 同时建立了一个多目标的优化模型, 不仅考虑了最大化拦截敌方威胁和最小化己方损失, 还考虑了最大程度保护己方重要舰艇。Silav等(2019)[40]主要考虑了海军编队舰对空导弹的重调度问题, 假定初始目标分配被不可预知的变化所打乱, 为了生成一个新的目标分配表, 提出了一个双目标的优化模型, 最大化无泄漏概率值, 并最小化与初始目标分配的总偏差。
1.1.3 空中拦截
空中拦截主要是指空对空拦截, 即己方战斗机或者无人机拦截敌方空中目标, 敌方目标主要包括敌方的无人机或者战斗机及其发射的武器。肖冰松等(2010)[41]对编队内飞机协同超视距空战条件下进行中远距拦截的目标分配问题进行了研究, 最大化拦截敌方的威胁。Bayrak等(2013)[42]研究了空战中的WTA问题, 主要考虑如何将有限的资源分配给目标以实现最大化的拦截效用。Shalumov等(2017)[43]分析了多个移动目标(飞机)、目标防御者和攻击目标的导弹之间的协同拦截场景, 其中受保护的资产为己方飞机。
1.1.4 协同空战
协同空战是无人机或者战斗机相互协同对抗的典型作战样式之一。协同空战首先强调团队的配合, 其次由于空战过程中弹药无法及时补充以及燃油有限, 因此还需要注重使用有限的武器打击一定的敌方目标。Peng等(2017)[44]研究了对动态多目标协同空战的WTA问题, 采用了“射击-观察-射击”的交战策略, 不仅考虑了时间窗口, 而且还提出最大化摧毁敌方和最小化消耗成本的双目标优化求解方案。Chang等(2017)[45]基于战斗力潜力的概念研究了协同空战的WTA问题, 使目标的总杀伤力最小, 其核心变量是相对优势。Li等(2018)[46]将武器对目标的杀伤概率和武器的消耗成本两个主要因素融入到一个单目标WTA模型中, 研究了空战武器对目标的优化分配, 以最小化敌方的加权累计威胁概率之和。Hu等(2018)[47]基于4个不同的威胁函数分别讨论了不同模型下协同空战的WTA问题。Pan等(2019)[48]主要关注协同空战中敌方火力攻击和电子干扰引起的对抗和不确定性, 以两个战斗队进行的非合作零和博弈模型来描述这种对抗, 同时考虑了与传感器的配合, 提出了一种改进的传感器数据融合方法以应对不确定性。
张涛等(2013)[49]、王网琴等(2014)[50]和马滢滢等(2022)[51]研究了超视距协同空战的WTA问题。文献[49]主要分析了超视距协同空战下敌机对己方的威胁系数的计算方式, 综合考虑了角度、速度、距离和隐身4个威胁因子和一个角度惩罚因子, 以最大化击毁敌机累计威胁概率为目标函数。文献[50]主要考虑速度、角度、高度、距离和能力5个优势因子作为威胁的影响因子, 以最小化敌方剩余威胁为目标函数。文献[51]从博弈论角度将超视距空战中的多无人机WTA问题建模为双矩阵博弈模型, 并将其转换为混合整数规划优化模型进行求解, 以反映超视距空战中的强对抗性。顾佼佼等(2015)[52]构建了多目标决策模型, 在达到毁伤阈值的前提下, 同时对一次攻击后使敌编队的总期望剩余威胁最小和导弹消耗量最小两个目标函数寻优。侯满义等(2017)[53]分析了无人机作战的约束条件, 综合考虑了多无人机协同作战下敌我双方的优势和威胁能力指数, 以最大化打击敌机的收益为优化目标。
1.2 进攻作战
1.2.1 地对地打击
地对地打击是现代战争的重要作战样式之一, 通过调用地面武器如火炮或者导弹攻击敌方目标。敌方目标主要包括军事装备、重要建筑、设施等。Sapaz等(2011)[54]研究了火炮目标分配问题, 考虑了目标、所用火炮类型以及离散时间等三要素。Cha等(2010)[55]对野战火炮火力调度问题进行了研究, 即给定的火炮单位对给定的目标进行打击的调度优化, 考虑了时间窗口, 并假设目标随着时间的推移, 火炮的击中概率逐渐下降。Choi等(2018)[56]主要研究了不确定条件下火炮射击顺序问题, 提出了一种火炮射击顺序的优化方法。
张信启等(2009)[57]研究了常规战略导弹打击的优化问题, 提出了战略导弹打击的目标点和瞄准点的计算方式, 以将有限的战略导弹在恰当的时机打击到敌方重要的目标。王然辉等(2016)[58]、Wang等(2019)[59]和Fu等(2019)[60]基于成本的角度研究了地面打击目标分配问题, 在满足目标伤害的前提下, 考虑了目标被击中的累计损毁, 以武器消耗的总成本最小化为目标函数。
1.2.2 空对地打击
空对地打击是出现较早的作战样式之一, 随着科技的进步和武器系统的升级, 现代的空对地打击也越来越复杂, 高效的目标分配, 不仅可以最大化打击敌方有生力量, 还可以节省武器消耗成本。彭星光等在2008年[61]和2010年[62]都针对无人机编队协同打击联合目标的优化问题进行了研究, 所建的模型反应出攻击方与被攻击方的内在关系, 前者主要考虑SWTA问题, 后者主要研究DWTA问题。Shima等(2009)[63]研究了无人机协同攻击地面移动目标的问题, 即多架无人机通过制导以及携带武器分工协作, 同时打击多个地面移动目标。吴文超等(2011)[64]研究了多无人机打击诸如敌方防空武器等背景下的软武器分配问题, 软武器是指无人机携带的干扰弹、电子干扰机等。刘毅等(2010)[65]分析了攻击无人机的协同目标规划问题, 主要构建了基于双层规划的任务分配模型, 其中融合了资源分配和航线优化两个子问题, 总体目标是保证攻击无人机作战的收益最大, 代价最小。
Deng等(2013)[66]研究了多异构无人机协同打击地面目标的多任务分配问题, 异构性是指不同无人机的功能不同、作战特点不同以及携带的武器不同。Dirik等(2015)[67]重点分析了空中打击地面目标的效率, 即给定一组地面目标集, 在每个目标都能达到其期望毁伤要求的前提下最小化打击总成本, 建立一个连续的两阶段优化模型优化打击分配方案。Zha等(2015)[68]研究了多无人机协同对抗对目标的优化问题, 从博弈论的角度出发, 分析了不完全信息下的动态多方对抗博弈在多无人机系统中的应用。Wang等(2017)[69]以战斗机携带的空对地导弹打击地面移动目标为应用背景, 提出了一种最大化打击敌方目标的模型。
Li等(2017)[70]主要研究静态的双目标战机打击地面目标问题, 该问题的目标是找到一个合适的静态任务, 使敌方的期望损失最大化, 同时使导弹的成本最小化, 为了更加接近真实的空战, 在建模时加入了飞行员的能力因素。Li等(2018)[71]在前期打击地面目标优化问题的基础上, 建立了一个三目标的优化模型, 考虑了战斗机的价值。Gao等(2019)[72]针对文献[71]中的空地打击场景, 将第3个优化目标中最大化战斗机价值调整为最小化战斗机损失。
1.2.3 反舰
战舰作为重要的战斗武器在战争中特别是海战中发挥着重要作用, 反舰作战作为海上作战的重要作战样式之一, 主要是指运用鱼雷、反舰导弹等武器打击敌方战舰, 最大化减少敌方战舰的威胁乃至摧毁敌方舰艇。反舰作战通常是一个多轮次的攻防过程, 这个过程既要考虑打击敌方舰艇也要考虑武器消耗。杨飞等(2010)[73]研究了多目标反舰导弹饱和攻击的优化问题, 以最大化打击敌方舰艇的效益、最小化己方武器消耗为目标, 并将航路规划与火力分配相结合, 提出了一种多发射、多约束条件下对敌舰队饱和打击的方法。
1.2.4 装甲对战
装甲对战是陆军作战的一种作战样式, 在WTA时具有自身特点。首先装甲部队机动性较强, 命中率存在较大的不确定, 其次装甲车辆命中毁伤性的估计较为困难。王正元等(2003)[74]研究了坦克对战中离散多阶段WTA问题, 双方的目标均是最大化消灭敌人, 最小化自己的损失, 分别讨论了摧毁一辆坦克的不同炮弹数、不同的击中概率以及有无累计效应等条件下一方取胜的DWTA策略。白帆等(2012)[75]主要基于模糊火力适度的原则讨论了坦克编队对战的WTA问题, 主要根据集火打击的特点, 结合模糊命中概率, 形成无约束的坦克对战的SWTA模型。常天庆等(2015)[76]结合动态装甲分队对战的特点, 以效用最大化为优化目标。陈军伟等(2016)[77]分析了装甲分队火力打击战法的运用方式及其对分配结果的影响, 建立了一种面向装甲分队战法运用的两阶段WTA模型。
1.2.5 联合火力打击
联合火力打击是多军兵种的多种武器联合打击敌方多个目标的典型作战样式。孔德鹏等(2016)[78]和徐克虎等(2016)[79]研究了合成分队的WTA问题, 合成分队是以信息化装甲武器平台为主的多种兵力合成的地面新型作战力量, 本质上是解决多兵种联合火力打击的火力优化问题。前者从静态的角度提出了基于主从决策的双层WTA模型, 后者从动态的角度, 基于自适应协同决策体系, 实现动态火力协同分配。刘双双等(2017)[80]以最大费效比和最小附带损伤为优化目标, 建立了针对联合火力远程打击的WTA模型。陈曼等(2019)[81]基于累计失败概率最低和使用武器成本最少原则, 研究了舰载武器联合火力打击的双目标WTA问题。孔德鹏等(2019)[82]主要研究了“点对点”突击和远程火力覆盖支援相结合的协同火力打击WTA问题, 以对抗双方剩余价值的比值为优化目标。田伟等(2020)[83]研究了基于随机时间影响网络的联合火力DWTA问题, 综合考虑了使命达成概率最大化、剩余战斗力最大化、行动时长最小化等原则, 分析了使命达成效果的非解析表达。
1.3 小结
不同的作战样式各有其特点, 本文对不同的作战样式的问题特点进行简要归纳, 如表 1所示。在分析问题规模时, 以常用场景为主; 在分析问题复杂性时, 由于WTA本身就是NP-hard问题, 因此对不同作战样式的相对复杂程度进行了简要对比。同样, 在时效性方面, 也是以常用作战应用场景为主。WTA问题还可以支撑战争问题研究、装备论证等, 这类场景对最优性的要求一般优于时效性方面。
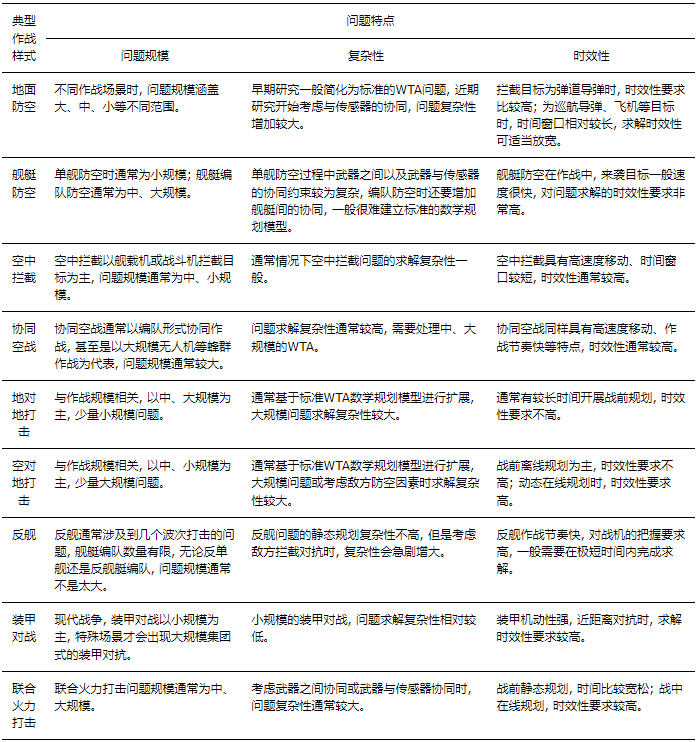
随着军事装备的升级以及计算机技术的快速发展, 特别是传感器等技术的应用, 不同的作战场景对WTA带来了新的挑战。首先, 更加关注问题模型化的过程, 所建模型需要反应作战场景的特点, 模型简化和假设方面逐渐向实际作战场景靠拢, 更加关注不确定性的影响。其次, 更加关注大规模作战的问题求解, WTA的痛点之一就是难以针对大规模的WTA进行高效高质量的求解。最后, 关注不同作战样式的时效性, 对相关WTA求解算法的效率提出了进一步要求。
2 建模方法
WTA问题经过多年研究, 已经发展出多个重要的分支方向与应用领域。根据不同领域特点, 数学规划、博弈论、图论、马尔可夫决策等多种方法被用来对WTA问题进行描述建模。表 2对不同建模方法的特点和重点应用领域作出了总结。
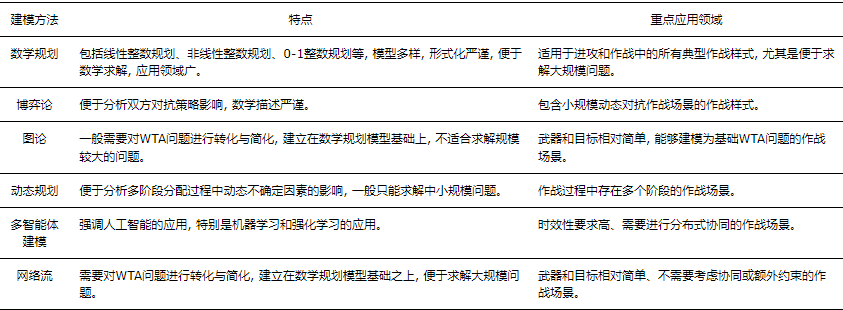
2.1 数学规划
数学规划是WTA问题的基础建模方法, 也是应用最广泛的建模方法。在WTA问题中最早提出的数学模型就是非线性整数规划模型。Manne (1958)[1]最早建立的模型就属于非线性整数规划模型, 是基于概率和非线性的形式来表述的, 但可以应用线性模型来近似描述。Lloyd等(1986)[2]证明WTA的基础整数规划模型属于NP-complete问题。至今, 数学规划模型仍在WTA领域发挥着重要作用。
WTA问题的基础静态数学规划模型如下所示:
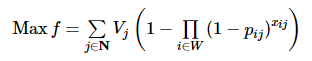
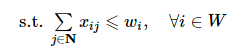
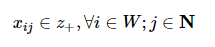
式中: Vj是目标价值; pij是武器i对目标j的毁伤概率; xij是决策变量, 即武器i分配给目标j的数量; wi是武器i的最大数量。式(1)为目标函数, 最大化打击敌方目标价值; 式(2)和式(3)是约束条件, 规定决策变量为正整数以及武器i可用的数量有上界。在此基础之上衍生了很多数学规划模型, 更多SWTA和DWTA数学规划模型可参考Kline等(2019)[6]的综述文章。
Lee等(2003)[84]提出了一个具有武器约束限制的非线性整数规划模型。Bayrak等(2013)[42]应用0~1背包问题对空战机队打击目标问题进行简约, 实验结果表明在小规模问题中能够获得最优解。Dirik等(2015)[67]为了解决战斗机目标分配问题提出了一种两阶段混合线性规划建模方法。Stieber等(2015)[85]将多武器对多目标分配问题看作是一个带移动目标的多旅行商问题, 建立了一个整数线性规划模型。Peng等(2017)[44]基于目标毁伤概率区间和时间窗约束, 提出了一种新的协同空战DWTA多目标整数优化模型, 该模型将目标毁伤效率最大和弹药消耗最小作为两个竞争目标函数。Li等(2017[70]、2018[71])提出了一个联合整数规划模型求解多目标的WTA问题。Hu等(2018)[47, 86]针对协同空战中的WTA问题, 提出了双方威胁函数的概念, 分别建立了线性整数规划模型和非线性整数规划模型。陆一平等(2019)[87]通过限定对目标分配武器的数量来降低整数线性规划模型的维数, 提高问题求解的效率。Xin等(2019)[88]为传感器-武器-目标分配问题建立了一个有约束的0-1整数规划模型。Li等(2019)[89]对SWTA问题的模型进行了总结, 建立了考虑传感器和武器细节的整数规划模型。Lu等(2021)[90]将WTA问题转化为一个具有二进制列的线性整数规划模型。
2.2 博弈论
博弈论方法是将敌我双方对抗策略的影响融入到WTA中。对抗双方会根据掌握的信息, 结合对方可能采取的所有行动和获得的效用构造支付矩阵, 寻找均衡策略, 进而制定下一步的WTA策略。因此, 博弈论成为DWTA问题的重要研究方法之一。
Soland等(1973)[7]提出使用博弈论中的双人零和博弈对WTA问题进行建模, 假设双方参与人通过探测系统或者情报信息得知对方的武器/目标数量、类型、杀伤力等信息, 但是不了解对方会在每个阶段采取的策略, 防御方/进攻方选取不同的策略准则计算支付矩阵, 寻找均衡策略。Zha等(2015)[68]建立了多无人机目标分配的不完全信息动态对抗博弈模型。Pan等(2019)[48]根据对抗博弈WTA模型的特点, 提出了一种分解协同进化算法来获得非合作纳什均衡策略。
张毅等(2012)[91]建立了一种具有距离折算因子的模糊-灰色非合作纳什博弈模型, 并将之转化为二次规划模型进行求解。Leboucher等(2014)[92]使用进化博弈的方法解决多目标DWTA问题中选择适应度的问题。Golany等在2015年[93]和2017年[94]研究了分配多个防御资源以保护多个站点免受对手可能攻击的问题, 建立了一个多行动集的两人零和博弈模型, 比较纳什均衡与非竞争环境下均衡解的结构, 分析了多阶段博弈过程策略调整对于博弈结果的影响。王邑等(2016)[95]使用Epsilon-Nash策略替代了传统纳什均衡搜索策略来寻找自主空战任务分配问题的纳什均衡点。Han等(2016)[96]考虑了一个更复杂的博弈场景, 建立了三阶段(防御方-攻击方-防御方)的完全信息零和博弈模型。张先剑(2019)[97]构建了基于双方动态博弈的攻防对抗综合数学模型。
2.3 图论
图论方法解决WTA问题时, 是在数学规划模型的基础上进行转化, 与图论紧密联系的是匈牙利算法, 用于寻找最优匹配方案。黄力伟等(2007)[98]针对目标函数是线性或非线性的一类火力分配问题, 提出了虚拟火力单位或目标的方法, 将问题转化为能够用匈牙利算法求解的指派问题。Leboucher等(2013)[99]利用拦截几何概念提出了一种最优的WTA方案, 在其另一项研究中(2014)[92], 设计了一个基于不对称二分图模型的匈牙利算法, 结合遗传进化博弈的思想解决多目标DWTA问题。Hamzehi等(2019)[100]通过强化学习解决了一个常见的组合优化问题, 即基于图的成对分配、最大二部基数匹配、最小割或最大和问题, 对使用图论方法进行武器目标分配很有借鉴意义。
2.4 动态规划
在实际作战过程中, 现阶段的行动决策影响着未来数个阶段的火力分配方案, 进而决定整个战斗的作战效果。因此, 需要考虑当前武器目标分配方案对未来状态的影响, 动态规划方法作为运筹学领域求解多阶段优化和决策过程的重要数学方法, 被广泛用来建立DWTA问题的模型。主要的研究方法是多阶段建模, 如Ahne等(2015)[101]、Xin等(2011)[102]和马尔可夫决策过程分析方法如Summers等(2020)[103]以及Davis等(2017)[16]。
在DWTA的场景中, 由于攻防阶段和打击效果的不确定性, 防御方/攻击方不得不考虑每一阶段需要发射和保留多少武器, 高维数的解空间使得传统的动态规划很难用于实际的场景。Ahner等(2015)[101]提出了一种自适应的动态规划方法, 解决两阶段DWTA问题。
Davis等(2017)[16]建立了离散小波变换的马尔可夫决策过程模型, 并采用近似动态规划方法求解。Menq等(2007)[11]利用离散时间马尔可夫过程模型解决多层弹道导弹防御方案优化问题。Summers等(2020)[103]利用近似动态规划方法建模, 并基于两种近似算法制定分配策略, 解决大规模WTA问题。
2.5 多智能体建模
随着人工智能技术的快速发展, 对多智能体方法的关注越来越多。多智能体充分发挥智能化的优势, 让繁琐的工作更加自动化、智能化地完成, 便于求解复杂约束的WTA问题。王玮等(2009)[32]为舰艇编队WTA决策提供了一种新的思路, 以编队分布式协同作战为典型场景, 建立了一种基于多智能体的WTA模型。李相民等(2010)[33]、陈华东等(2010)[34]以及李亦伟等(2010)[35]也研究了基于多智能体的WTA问题。文献[33]提出了一种异步并行蚂蚁智能体系统模型, 文献[34]设计了一种多智能体辅助决策系统, 文献[35]考虑了舰艇编队防空武器之间的软硬火力配合, 建立了软硬武器兼容约束判断模型。Wang等(2015)[13]设计了一个自适应神经网络结构, Shalumov(2017)[43]在线性制导律的基础上提出一种协作制导律, 解决多智能体拦截多目标的问题。
2.6 网络流
网络流是求解WTA问题的一种可选方法。Castanon等(1987)[104]建立了WTA问题的非线性网络流模型。Ahuja等(2007)[105]将WTA问题建模为整数规划问题和广义的整数网络流问题, 辅助寻找最优解的下界, 提出利用分支定界技术求解WTA问题的精确算法和启发式算法, 该方法可以即时找到中等规模80个武器、80个目标,记为(80W*80T)算例的最优解, 也可以在数秒内求出较大规模(200W*200T)算例的满意解。Chang等(1987)[106]通过对非线性问题进行线性近似, 建立了求解SWTA问题的迭代线性网络规划模型。
2.7 其他方法
除上述建模方法外, Burr等(1985)[107]提出了一个用于特定军事领域资源分配的专家系统, 整合了几种人工智能重要技术的变体, 并将考绩规则应用于WTA。Wacholder(1989)[8]应用神经网络方法解决弹道导弹防御中的WTA问题。Yang等(2017)[108]、Sahin等(2014)[109]提出基于模糊数学理论建立多目标规划WTA模型, 并利用不确定性理论的必要度原理, 求解带有模糊参数的不确定性WTA问题。Choi等(2017)[110]建立了一个两阶段模型, 先确定射击顺序, 再通过鲁棒性优化方法调整不确定因素带来的影响。
3 求解算法
由于WTA问题的NP-complete特性, 研究高效的求解算法一直是该领域的研究重点与难点。当前的求解算法主要分为精确求解算法和近似求解算法, 其中近似求解算法又包括基于规则的启发式算法、拉格朗日松弛方法、元启发式算法以及机器学习等算法。主要算法分类如图 2所示。

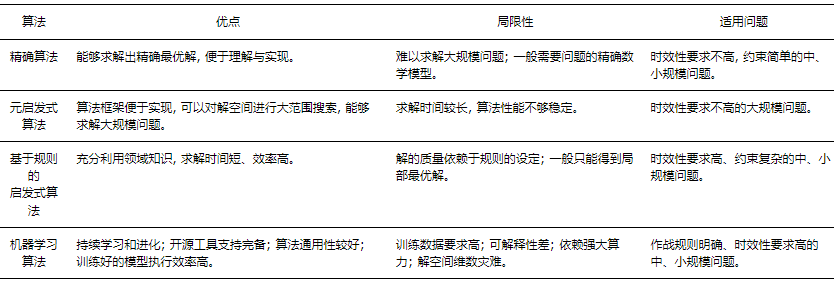
不同类型算法的优点、局限性以及适用问题如表 3所示。其中, 无论精确算法还是近似算法都可以用来求解WTA数学规划模型和动态规划模型, 机器学习算法还可以求解博弈论、网络流、图论模型和多智能体模型。包含各种智能优化算法的元启发式算法, 研究的最多。一方面, 人工智能的快速兴起与发展也给WTA问题提供了新的研究契机, 结合当下无人作战、蜂群作战的特点, 建立适合无人作战、跨域联合作战的模型将是未来的进一步研究方向。另一方面, 目前研究WTA的算法非常多, 缺乏普适的算法框架与平台, 需要构建一些通用性较好的、便于执行的典型算法库, 同时进一步探索人工智能技术的应用, 研究线下深度学习与线上快速优化相结合的智能算法是未来的重要发展方向。
3.1 精确算法
精确算法通常只能求解小规模的问题, 并且在问题假设方面通常会进行适当简化。Denbroeder等(1959)[111]假设任何武器击中同一目标的概率相同, 并且目标同质, 使用最大边际收益(maximal marginal return, MMR)算法将武器均匀分布在尽可能多的目标上, 实现武器目标的最优分配。Soland等(1973)[7]设计了隐式枚举方法与分支定界相结合的求解算法解决防御方反弹道导弹部署问题。
分支定界算法是求解WTA问题的主要精确方法。Rosenberger等(2005)[112]对比了连续拍卖算法和分支定界方法求解WTA问题的效果, 结果显示当单一目标可以被分配多个武器时, 分支定界方法能够快速解决小规模WTA问题。Ahuja等(2007)[105]给出了3种求解武器目标分配最优解下界的策略: 广义网络流策略、最小成本流策略和MMR策略, 在分支定界算法中引入这些下界策略, 提高了分支定界搜索的效率。Kwon等(2007)[113]提出了一种分支和定界算法求解WTA问题, 该算法是分支与定界算法的推广, 允许在整个分支和定界树中应用列生成, 初始列的生成采用贪婪的启发式方法。Cha等(2010)[55]设计了野战炮兵火力调度的分支定界算法, 可以在合理的时间内找到中等规模问题的最优解。Kline等(2019)[114]设计了一种基于混合深度优先选择策略的分支定界算法, 解决了较小规模的非线性整数规划WTA问题。
Bogdanowicz等(2009)[115]针对带有传感器的WTA问题, 在拍卖算法的基础上提出了一种新的精确求解算法, 并证明该算法可以在有限步骤内收敛于最优解。Li等(2011)[116]改进了基于拍卖算法的传感器-武器-目标优化(sensor-weapon-target optimization, Swt-opt)算法, 将改进的Swt-opt与一致性算法相结合, 避免了网络拓扑限制, 实现了传感器WTA问题的求解, 同样证明该算法可以在有限步骤内收敛于最优解。Lu等(2021)[90]提供了一种快速求解大规模WTA问题的精确方法, 将WTA问题建模为0-1整数线性规划模型, 并应用列生成以及分支定界方法求解, 同时为了大幅度减少需要枚举的列数, 提出了一种武器数量界限和武器支配的处理方法以减少计算过程中需要枚举的列数。
Sikanen等(2008)[117]采用了动态规划的方法求解出小规模案例(10W*10T)的精确解。Ahner等(2015)[101]针对两阶段DWTA问题提出了一种自适应动态规划算法, 该算法融合了凹自适应值估计(concave adaptive value estimation, CAVE)算法、MMR算法和改进的MMR(MMRPlus)算法, 借助后决策动态规划公式和CAVE函数逼近方法, 证明了所提算法解的最优性。
3.2 近似算法
3.2.1 基于规则的启发式算法
在WTA过程中, 指挥员的决策偏好、作战样式/武器目标的领域知识等可以转化为辅助构造优化方案的规则。基于规则的启发式算法是在WTA方案的构造和搜索过程中, 充分利用这些规则, 快速生成较优的可行解。其优点是时效性强, 能够很快得到问题的优化解; 缺点是依赖场景和领域知识, 容易产生局部优化解。
Burr等(1985)[107]提出了一种求解单目标多阶段WTA问题的最优算法, 该方法计算第一阶段防御拦截器的最小数量, 以确保来自一个攻击者的损害期望值不超过1, 后续阶段的攻击者的损害期望值不超过1/k。迭代步骤假设k-1阶段攻击武器已被分配给拦截器, 然后计算分配给k阶段攻击武器的拦截器的最小数量, 其服从通常的边界约束。Soland等(1987)[118]研究了动态交战WTA问题的最优解, 最优解交战策略是关于攻击武器、拦截器以及剩余交战次数的函数。求解的核心思想是将部分拦截器分配给目标, 根据交战结果将剩余拦截器分配给剩余目标, 形成一种射击-观察-射击的交战策略, 随着交战过程的不断迭代, 目标是最小化攻击后剩余拦截器的预期数量, 同时也可以求解出为目标提供所需保护级别的最小拦截器数量。
Schultis(1978)[119]提出的渗透算法解决了分层区域防御中武器向目标的最优分配问题, 渗透算法核心思想是通过约束攻击者的击中概率和防御者的拦截概率都小于1并允许向下渗透, 从而实现最优攻击。Orlin(1987)[120]引用了文献[119]的算法和模型, 同时提出了消耗算法, 与渗透算法作对比, 消耗算法与渗透算法都是实现最大价值的打击策略, 不同的是消耗算法假设没有渗透, 在确定最优策略时必须要考虑最外层防御, 即摧毁或消耗掉外层的防御武器才向下层攻击。文献[120]还针对这两种算法的特点提出了混合算法, 特别是消耗算法引入概率会消除一些整数解, 从而很难找到最优解。混合算法首先利用消耗算法求解原问题, 然后使用Schultis公式计算泄漏, 逐层分析输出信息, 混合算法可以减少攻击武器的数量并获得最大值攻击。
Lee等(1994)[24]提出了一种将归纳学习融入仿真建模的有效方法来分析舰艇防空作战场景, 能够从示例集中自动归纳规则, 在模拟环境中使用归纳法, 能够在舰船防空评估模型中发现关于最优武器分配的规则。潘书山等(2005)[121]将已有的历史数据、经验和相关的知识归纳为WTA规则, 并借助粗糙集理论和线性规划理论进行定量与定性分析。Mekawey等(2009)[122]通过分析影响分配效果的相关因素, 提出了威胁优先级规则和武器价值-威胁规则, 并融入顺序搜索算法和匈牙利算法, 在小规模实验中, 能够得到接近最优的分配方案。
Xin等(2011)[102]设计了一种基于规则的启发式构造算法求解DWTA问题, 在可行解生成过程中, 通过动态验证不同约束的饱和状态, 实现武器分配过程中的约束满足。Sahin等(2014)[109]将近似推理理论应用于WTA算法, 设计了一种基于规则的映射, 采用网格划分方法生成规则库。通过训练数据集产生模糊决策者, 以快速作出WTA。彭彰(2013)[123]分析了指挥人员的作战指挥规则, 并将不同作战场景下指挥人员的指挥规则、我方武器情况输入到数据库, 当战斗发生时, 基于敌方目标威胁大小, 快速构造WTA方案。刘兴林(2015)[124]提出一组适应舰艇火力通道组织的火力分配规则, 设计了基于规则评价的算法, 可以使目标分配结果与规则的符合度直观明确, 更符合指挥员的决策思维过程。Chang等(2018)[125]提出了4种基于规则的启发式因子的初始化方法, 分别为基于武器选择优先权的启发式因子、基于目标选择优先权的启发式因子、基于随机序列的目标选择优先权的启发式因子和基于坎尼金定律的启发式因子, 提高了初始解的构造质量。Xin等(2019)[88]提出了一种基于边际收益的构造式启发式(marginal-return-based constructive heuristic, MRBCH)算法, 以解决公式化的传感器-武器-目标分配问题。
3.2.2 元启发式算法
3.2.2.1 单点迭代搜索算法
单点迭代搜索算法在每次算法迭代过程中以单一解为基础生成另外一个解, 可以看作在解空间中一个点一个点的搜索、跳跃, 来逐步改进当前解。主要的单点迭代算法包括SA算法、TS算法和VLNS算法等。
Jaiswal等(1993)[126]提出求解WTA问题的SA算法。Madni等(2009)[127]实现了SA算法在较短时间内求解出大规模WTA的次优解。Sonuc等(2017)[128]提出了并行SA算法求解WTA的问题, 算法实现了计算机的并行处理, 提高了运算效率。Xin等(2010)[129]提出了基于虚拟排序和TS的启发式算法, 通过多类型约束的虚拟排序, 并融入TS过程, 来求解DWTA问题。
VLNS算法是解决大规模WTA问题的有效方法之一。Ahuja等(2007)[105]首先实现了VLNS算法解决WTA问题, Lee等(2010)[130]采用VLSN算法解决了受约束的WTA问题, 所谓受约束是指防御方针对敌方武器可用拦截器数量有上界和下界以及总的拦截器数量有上限, 两者都实现了几秒内求解多达100个武器100个目标的大规模WTA问题。
Tokgöz等(2013)[131]分别使用GA、TS算法、SA算法和变邻域搜索(variable neighborhood search, VNS)算法实现了SWTA问题的求解, 并对算法的效率和质量进行了比较。
3.2.2.2 种群迭代搜索算法
随着科学技术的发展特别是计算机技术的发展, 运筹优化领域出现了越来越多受生物启发的仿生智能优化算法, 主要包括GA、PSO算法、ACO算法、人工蜂群(artificial bee colony, ABC)算法、灰狼优化(gray wolf optimization, GWO)算法、人工鱼群算法(artificial fish swarm algorithm, AFSA)以及和声搜索(harmony search, HS)算法等。
(1) GA
遗传算法是求解WTA问题的常用算法之一, GA不仅用于求解单目标问题, 经过改进的GA也可用于多目标WTA问题。
1) 求解单目标的GA
Metler等(1990)[132]首次提出将GA应用于求解WTA问题, Lee等(2002)[133]改进了GA, 将特定领域知识融入交叉算子和局部搜索机制, 提出了一种精英保留算子交叉策略, 保留那些可能较好的基因, 剩余的基因用于随机交换以产生后代; 其次采用局部搜索策略代替随机搜索策略, 使用贪婪重组方案来寻找在当前解附近适应度更高的可行解。Lee等(2003)[84]进一步将GA中的局部搜索方法表述为优生过程, 并将文献[133]中提出的贪婪重组方案搜索策略表述为贪婪优生学, 给出了一种改进的贪婪优生学遗传算法, 用于求解一般的WTA问题。Lu等(2006)[134]在求解海军舰队目标分配模型时, 对GA在初始种群均匀创建、适应度尺度选择、遗传算子自适应参数等方面进行了改进, 引入了扩展汉明距离作为初始种群均匀的判断方法, 采用西格玛截断标度公式作为适应度选择依据, 并设计了新的变异概率和交叉概率更新公式。
Wu等(2008)[135]针对受时间约束的DWTA提出了目标分配时间界限的概念, 将其融入到普通GA中, 并在运行过程中采用多轮次执行方式以模拟动态过程。Song等(2009)[136]在求解整数线性WTA模型时, 提出了一种初始种群改造方法, 贪婪地寻找一个更好的初始种群作为父种群, 以便更早地收敛, 并将这种算法命名为启发式遗传算法。
Li等(2009)[137]考虑到武器分布的空间位置, 武器目标不能随意匹配, 将不能配对的武器目标表述为“禁止位”, 为GA中的二进制染色体矩阵设计了一种新的禁止位遗传算子, 称为“圈交换”算子, 交叉和变异操作可以基于“圈交换”算子来执行, 提高染色体在整个进化过程中产生可行解的有效性。Chen等(2009)[138]提出了求解DWTA问题的模因算法, 该算法本质上是一种改进型GA, 又名为遗传局部搜索算法, 是对初始群体、交叉和变异之后的个体运用局部搜索策略, 设计了贪婪局部搜索和最速局部搜索两种策略。Deng等(2013)[66]针对多异构无人机协同打击的多类型协同任务分配问题, 提出了一种改进的多型基因GA, 基本思想是在任务类型的基础上对染色体进行编码, 为每种类型的基因设计包括初始化策略、交叉算子和变异算子。
Li等(2019)[89]提出了一种求解传感器-武器-目标分配问题的改进遗传算法, 采用十进制编码方式, 编码长度为武器数量与传感器数量之和, 基于规则进行种群初始化, 并设计了遗传操作修复算子, 将遗传过程中产生的不可行个体修复为可行解。Wang等(2019)[59]为遗传算法设计了一种变值控制方法, 通过对变量取值范围进行控制来提高搜索效率, 在遗传算法初始化过程中缩小变量取值范围以缩短计算时间, 在变异过程中放大变量取值范围以保证多样性。Fu等(2019)[60]为了克服遗传算法初始化的困难, 提出了一种可变概率分配技术, 首先用可行解确定变量值的概率分布, 然后用概率分配模式代替随机均匀分配模式初始化变量, 产生接近最优个体的初始种群个体。
2) 求解多目标WTA的GA
经过改进的GA同样适用于求解多目标WTA问题, 如非支配排序遗传算法(nondominated sorting genetic algorithm, NSGA)、带精英策略的快速NSGA(NSGA-Ⅱ)和NSGA-Ⅲ等。NSGA-Ⅱ相比较于NSGA做出了3个方面改进, 首先提出了快速非支配排序法, 降低了计算复杂度; 其次引入了GA精英策略, 提高了解的质量; 最后提出了拥挤度和拥挤度比较算子, 代替了NSGA需要指定共享半径的适应度共享策略, 提高了种群的多样性。NSGA-Ⅲ相比较NSGA-Ⅱ, 后者根据拥挤度来选择个体, 前者根据参考点来选择个体, 参考点是在空间中均匀地选择点位置, 提高了NSGA-Ⅲ的多样性和收敛性。
Chen等(2012)[39]引入NSGA-Ⅱ求解了海军舰艇编队多目标WTA问题。Li等(2015)[139]在NSGA-Ⅱ中增加了自适应策略, 提出了一种相反的交叉率自适应机制, 将高交叉概率分配给好的解。Li等(2018)[71]针对NSGA-Ⅲ做了两方面改进, 首先是参考点生成策略, 利用当前种群提供的信息, 创建了一组在收敛和分布方面具有良好性能的参考点, 由于新参考点的增加, 算法的计算复杂度也相应增加, 又提出了参考点的消除机制; 其次是提出了在线算子选择机制, 自适应选择合适的策略来适应搜索环境并产生更好的结果。Gao等(2019)[72]同样对NSGA-Ⅲ进行了改进, 并用于求解三目标WTA问题, 首先提出了基于优势度矩阵的非支配排序, 以减少排序方案中不必要或重复的比较; 其次在选择个体时, 利用生态位信息和优势比来平衡多样性和收敛性。
多目标进化算法(multi-objective evolutionary algorithm, MOEA)也属于基于遗传思想的算法, 近几年, 部分学者引入基于分解的MOEA(multi-objective evolutionary algorithm based on decomposition, MOEA/D), 用于求解多目标的WTA问题。MOEA/D应用了分解思想来代替帕累托优势关系, 将一个多目标优化问题分解成多个标量优化问题, 这些问题通过使用预定义的权重向量进行聚合, 并同时对其进行优化。常用的聚合方法主要有3种: 权重聚合方法、切比雪夫方法和基于惩罚的边界交叉法。
Li等(2015)[139]在求解多目标的DWTA问题时, 提出了带有自适应机制的MOEA/D, 通过重新设计MOEA/D框架中子问题个体的交叉和变异概率公式实现自适应机制。Li等(2018)[18]改进了MOEA/D的框架, 首先设计了一种新的分解机制, 将种群分解为多个子种群, 并对交配约束机制和选择操作进行了改进; 其次提出了一种基于“先验知识”的种群初始化方法, 提高初始解的质量; 最后设计了一种改进的非支配解选择方法来处理帕累托前沿约束问题。Zhang等(2019)[140]提出了一种改进的MOEA, 首先为了帕累托最优集的完备性, 设计了一种计算复杂度低且不需要任何参数的自适应排序算法来保持种群的多样性; 其次提出了一种合作进化策略, 利用了相邻非支配解的相似性提高收敛性能; 此外, 还设计了不可行解评估策略和修复机制。Xu等(2020)[22]在求解不确定条件WTA鲁棒优化模型时, 提出了一种带启发式初始化的改进MOEA/D, 设计了一种基于费效比的多目标启发式初始化方法, 并对一般的MOEA/D框架进行了两个主要改进, 即基于最低点的切比雪夫方法和邻居匹配策略, 以增强后代的生成和选择过程。Li等(2021)[141]分别设计了基于自适应权重向量调解策略的MOEA/D和带有ε约束的MOEA/D, 用于求解多阶段WTA问题, 其中自适应权重向量策略是周期性地调整子问题的权重向量, 通过从拥挤区域中移除子问题, 并在稀疏区域中添加新的子问题, 从而获得更加均匀的帕累托前沿; ε约束方法是选择其中一个目标作为主要目标, 将其他非主要目标转化为约束, 并为每个非主要目标关联一个上限系数。
(2) PSO算法
PSO算法源于对鸟群捕食行为的研究, 粒子通过每一轮次更新自己的速度与位置, 向全局最优解靠拢, 直至满足算法终止条件。PSO算法不仅是求解单目标WTA问题的常用算法之一, 同时也是求解多目标WTA问题的主要算法之一。
1) 单目标PSO算法
Zeng等(2006)[142]首次将离散PSO(discrete PSO, DPSO)算法应用于求解WTA问题, 将贪婪搜索策略引入到DPSO算法中, 通过构造一个优先级集合来控制局部搜索并有效地收敛到全局最优, 为了避免陷入局部最优, 设计了一种“置换”更新策略。Thangaraj等(2009)[143]提出应用量子PSO(quantum PSO, QPSO)算法求解WTA问题, 将量子计算引入到PSO算法中, 假设空间中的粒子具有量子行为。该算法在保留粒子群算法优点的同时, 克服了过早收敛的缺点, 提高了算法的性能。Chen等(2012)[144]提出了基于遗传算子的PSO算法, 通过一种新的三层整数编码方式降低问题的复杂度, 实现问题的约束转化, 通过交叉、变异和选择算子来更新粒子。Zhou等(2016)[145]提出了一种DPSO算法来解决受射程约束、武器目标匹配约束等限制的WTA问题, 首先提出了一种新的编码方式, 使得一种武器可以攻击多个目标, 一个目标也可以受到多个武器攻击; 其次将GA中的均匀变异和交叉概念引入到标准PSO算法中, 生成DPSO算法的更新方程。Li等(2016)[15]改进了PSO算法, 用于多层弹道导弹防御WTA问题, 通过在基本算法中嵌入反向预测器来避免早熟收敛, 并加入排斥力来保持多样性。Wang等(2017)[146]提出离散PSO的直觉模糊熵概念, 并将其应用于DWTA求解, 定义了选择粒子群直觉模糊参数的策略, 将直觉模糊熵作为度量和速度变异的基本参数。
2) 多目标PSO算法
多目标PSO算法将帕累托前沿融入到PSO算法中。Zhou等(2016)[147]设计了一个两级进化多目标PSO算法求解多目标WTA问题, 采用了两阶段的进化策略, 在进化的第1阶段, 种群通过PSO算法中定义的粒子状态更新规则进行进化; 在进化的第2阶段, 设计了一种进化算子来更新第1阶段获得的帕累托解集。Peng等(2017)[44]应用混合多目标DPSO算法求解DWTA问题。首先, 在该算法中加入邻域搜索操作, 提高搜索能力和收敛速度; 其次, 引入删除和修复操作, 不仅可以修复不可行解, 还提高了可行解的质量; 此外, 采用柯西变异算子保持帕累托解集的多样性。
Xu等(2017)[17]提出带有双/单井的多目标QPSO算法, 用于求解不确定条件下防空和导弹防御的WTA问题, 该算法也是基于QPSO算法的改进型算法, 首先采用基于双井/单井的位置更新方法来平衡解的多样性、收敛精度和收敛速度; 其次为了避免早熟收敛, 设计了混合随机变异方法; 该算法还采用基于两阶段的引导粒子选择方法, 提高解集的分布均匀性和收敛速度。Fu等(2019)[148]提出了一种基于多种群协同进化的多目标PSO算法, 构建了主子种群协同进化模型, 每个子种群对应一个目标函数, 用于搜索非劣解, 主种群从子种群接收所有非劣解并修复非劣解之间的间隙, 生成相对最优的帕累托最优解集。Wei等(2019)[149]应用多目标DPSO算法求解考虑通信延迟和武器消耗的水下对抗WTA问题, 重新设计了符合该问题离散域特征的粒子位置和速度更新公式。
(3) ACO算法
ACO算法源自于自然界蚁群寻找食物过程中路径选择的智能行为, 也是求解WTA的常用算法之一。Wang等(2008)[150]将禁忌搜索算子的思想融入ACO算法中, 建立了ACO算法中的禁忌表并不断更新, 通过对路径选择、信息素更新和禁忌表更新的分析应用, 实现了求解WTA问题的蚁群算法。Shang等(2008)[151]主要解决了蚁群算法的并行机制运用于求解WTA问题, 群体间的启发式过程通过贪婪重组来寻找最优解。
Cao等(2018)[152]为了解决多层防御场景下大规模约束WTA问题, 基于Spark框架开发了一个分布式最大-最小蚂蚁系统(max-min ant system, MMAS)算法, 在标准蚂蚁系统的基础上设定了信息素的上下界, 最好的信息素用于增强解的收敛性, 最小的信息素用于探索解的多样性和可能性。Rezende等(2018)[153]将经典的确定性启发式算法MMR与蚁群系统(ant colony system, ACS)相结合, 设计了一种贪婪的蚁群系统(greedy ant colony system, GACS)算法用于求解WTA问题, 采用问题特定的信息素初始化启发式信息以及特定的选择策略。同时, 还应用了多群体并行策略来提高算法性能。Hu等(2018)[47]在求解WTA问题时, 从路径选择、信息素更新和信息素浓度区间等方面对传统蚁群优化算法进行了改进, 并提出了基于蚁群优化的精英策略, 信息素更新时, 精英蚂蚁得到奖励, 垃圾蚂蚁受到惩罚。
Li等(2017)[70]采用改进的多目标ACO算法求解双目标WTA问题, 设计了基于新设计算子的多目标ACO算法, 包括动态启发式信息计算方法、改进的移动概率规则、动态蒸发率策略、信息素全局更新规则和边界对称变异策略。
(4) ABC算法
ABC算法是模拟蜜蜂分工合作高效寻找食物而提出的群体智能算法, ABC算法的核心是雇佣蜂、非雇佣蜂(侦查蜂和跟随蜂)和食物源。其中, 雇佣蜂又名引导蜂, 非雇佣蜂是指侦查蜂和跟随蜂, 非雇佣蜂的职责是侦查探寻食物源以及根据引导蜂传递的食物源信息进而以其质量做出选择, 雇佣蜂职责主要是引导采蜜并将食物源信息传递给跟随蜂, 在整个搜索过程中, 雇佣蜂与非雇佣蜂之间的角色是相对的, 会发生转换。
Chang等(2018)[125]针对传统ABC算法收敛速度慢、易陷入局部极值等缺点, 从排序选择策略和基于精英引导的搜索方程两个方面对算法进行了改进, 并将其应用于DWTA问题求解。引导蜂的选择概率计算方面引入基于排序位置的选择方法, 每个个体的选择概率通过排名位置固定, 使得个体的选择概率不受适应度值变化的影响, 个体排名越高, 被选中的概率就越大, 同时排名较低的个体也有一定的概率被选中, 提高了ABC算法跳出局部极值的能力。选择群体中适应值最高的个体组成精英群体, 采用精英引导使种群快速收敛, 改进了搜索方程。Guo等(2019)[21]针对多对多导弹拦截的WTA问题, 设计了固定分组策略和基于惩罚函数的自适应分组策略, 应用ABC算法解决了具有分组约束的WTA问题。
(5) GWO算法
受仿生学的启发, 部分学者根据狼群搜索狩猎的习性提出了GWO算法。Pu等(2018)[154]设计了基于分布式拍卖机制(distributed auction mechanism, DAM)的GWO算法求解无人水面战车协同攻击的WTA问题, 在GWO算法中加入了DAM可以生成符合实际约束的初始解, 保证了灰狼的多样性, 而且避免了穷尽和陷入局部最优。此外, 还提出了相应的适应度函数来评价该算法的质量。Wang等(2018)[155]通过一种十进制编码方法和一种新的位置更新方法即模块化位置更新方法, 将原始的GWO转化为离散的GWO, 还采用了遗传算法中常用的精英保留机制, 以及一种避免局部最优的局部搜索算法, 提出了一种混合离散灰狼优化(hybrid discrete grey wolf optimizer, HDGWO)算法求解非线性整数规划WTA问题, 还在编码方法和局部搜索算法中引入特定的领域知识来压缩可行解空间。
3.2.2.3 混合智能搜索算法
混合智能搜索算法是将两种或两种以上的元启发式算法相结合, 集成各自的优点, 以提高问题的求解效果, 是求解WTA问题的重要方法。Khosla等(2001)[156]和Bisht等(2004)[157]将传统GA和SA算法相结合, 提出了一种新的混合GA来求解WTA问题。文献[156]采用SA型启发式算法来计算GA选择的种群的适应度, 用来求解DWTA。文献[157]集成了GA的全局交叉算子和SA算法的局部随机爬山特性, 用于提高算法的搜索效率。Lee等(2002)[158]结合了ACO算法在空间内的协同搜索以及避免过早收敛的优点和免疫系统(immune system, IS)在小区域内快速找到较好解的优点, 设计了基于免疫的ACO算法用于求解WTA问题。Zhang等(2012)[159]将GA和ACO算法相结合, 应用随机数和信息素更新策略来增加解的多样性, 引入交叉算子和变异算子来扩大搜索空间。Wang等(2011)[12]结合ACO算法求解的高效率和SA算法求解高质量的优点, 提出了求解WTA问题的蚁群-模拟退火混合优化算法。Yang等(2016)[160]将免疫系统集成到自适应GA框架中, 提出了一种自适应免疫遗传算法(adaptive immune genetic algorithm, AIGA), 设计了免疫接种算子和免疫选择算子, 前者使每个武器系统尽可能配对到毁伤概率最高的目标, 后者用于更新种群。Wang等(2017)[69]在文献[160]中AIGA算法的基础上, 对交叉算子和变异算子选择概率的自适应更新公式进行了改进。
人工鱼的行为主要有随机行为、追逐行为、群体行为和搜索行为, 这使得AFSA在全局搜索方面表现较好, 但在局部搜索方面表现较差。HS主要是模仿音乐演奏者的即兴创作过程, 其在解的质量上有很好的表现, 但搜索速度较慢, 对初始解的依赖性很强。Chang等(2017)[45]和li等(2018)[46]实现了改进的AFSA和改进的HS组成的混合算法求解WTA问题, AFSA的改进主要体现在初始化、视觉和运动策略以及跳跃行为。首先, 提出了一种混合初始化方法, 包括混沌、信息熵和基于对立的学习方法; 其次, 提出了一种伪并行进化策略, 将人工鱼群划分为多个子群体, 每个子群独立执行最优搜索, 并在每次迭代中与其他子群交换最优解, 以保持搜索空间并防止早熟; 再者, 提出了一种保持自身优势吸收其他优势相结合的游动策略; 此外, 视觉决定了AFSA算法的收敛速度和精度, 提出了包含随机数和修复机制的自适应视觉策略; 最后, 改进了鱼群跳跃行为概率和跳跃行为策略, 跳跃行为是为了避免陷入局部最优, 保持解的多样性。HS主要包括5个主要变量, 即和声库的空间大小、和声库的取值概率、微调概率、调整幅度和调整次数。HS的改进主要体现在新的和声库的取值概率生成公式和新的和声生成策略。两种改进型算法的切换通过两个方面实现, 即人工鱼的切换迭代和个体标准误差, 当满足设定的切换条件时, 改进的AFSA算法切换为改进的HS算法。
3.2.2.4 其他元启发式算法
差分进化算法与GA流程结构非常相似, 都包含初始化、选择、交叉、变异等, 操作算子的具体定义不同, Xue等(2014)[161]在传统的离散差分进化算法中引入自适应学习机制, 提出了一种基于自适应学习的离散差分进化算法, 实现了该算法求解电磁干扰WTA问题。Liang等(2016)[162]实现了自适应混沌并行克隆选择算法求解舰艇编队防空WTA问题, 该算法结合混沌理论和并行种群分类的优点, 以实现种群初始化和种群更新。Pan等(2019)[48]根据对抗博弈WTA模型的特点, 提出了一种分解协同进化算法来获得非合作纳什均衡策略。Silav等(2019)[40]提出了新的和替代性启发式算法以及改变和交换启发式算法, 实现了双目标导弹调度问题的求解。
Li等(2017)[163]提出了一种改进的差分进化算法求解考虑传感器的WTA问题, 实现了高效求解中等规模的高维优化WTA问题。Zhang等(2020)[23]提出了一种动态传感器/异构WTA的进化算法, 设计了3种编码方法来构建解个体, 实验显示了该算法具有良好的收敛性和实时性。
Zhang等(2015)[164]提出了一种新的求解DWTA问题的实时算法, 该算法流程框架类似GA, 能够对不确定环境下的动态任务进行实时决策, 提供任意时刻的满意解。Wang等(2016)[165]实现了一种基于克隆选择的优化算法求解DWTA问题, 克隆选择算法属于一种免疫算法(immune algorithm, IA), 在保证种群多样性的前提下, 具有很强的学习、记忆、进化等特性。Lai等(2019)[166]实现了一种改进的简化群优化算法求解DWTA问题, 该算法采用了用于种群初始化的确定性初始化方案和用于局部搜索的目标交换方案两种新方案。针对DWTA的“观察-定向-决策-行动”策略, Zhang等(2020)[167]在基于资产的DWTA(asset-based DWTA, A-DWTA)模型的基础上建立了一种新的基于滚动时域分解策略的A-DWTA模型, 设计了一种基于统计边际收益的启发式算法, 实现了该模型的求解。
3.2.3 机器学习算法
早在2000年时, 研究人员尝试应用机器学习类算法求解WTA问题, 但很长一段时间并没有引起广泛的关注。近年来, 随着人工智能技术的快速发展, 机器学习类算法重新受到WTA研究领域的关注。Bertsekas等(2000)[9]提出求解导弹防御问题的神经动态规划(neural dynamic programming, NDP)方法。NDP是一类强化学习方法, 通过使用基于神经网络的最佳成本-收益函数的近似来处理维数灾难, 其次不需要一个明确的系统模型而是使用模拟器作为模型替代品, 以便训练神经网络结构并获得次优策略。Azak等(2008)[168]针对威胁评估武器分配系统, 提出了多智能体协同混合学习方法, 采用人工神经网络的反向传播算法进行威胁评估, 设计了一种改进的Q-Learning算法进行武器分配。Mouton等(2011)[169]集成了强化学习领域的蒙特卡罗控制算法和非策略时差学习控制算法——Q-Learning学习算法, 并应用于求解防空WTA问题。Wang等(2015)[13]提出了一种新的带递归神经网络(recurrent neural network, RNN)控制器的自适应自组织映射算法, 可以实现防御导弹自动分配给来袭目标, 并设置监控器以减少与理想匹配的误差。王邑等(2016)[170]提出了机器学习领域基于类型2区间模糊k近邻分类器的DWTA方法, 采用分支定界算法产生的精确优化方案构造训练集, 并将解空间与训练集近似化, 从而推理出WTA方案。Gibbons等(2019)[171]提出了一种深度学习方法, 自动学习启发式规则以解决组合分配问题, 并以WTA问题对该方法进行了验证。Shojaeifard等(2019)[172]提出用投影RNN模型求解DWTA问题的方法。Jang等(2019)[20]针对敌方发射的来袭导弹, 引入机器学习的模型, 不断学习导弹飞行状态与命中概率之间的关系, 结合雷达预测的命中概率, 优化拦截武器的分配策略。
3.2.4 拉格朗日松弛方法
拉格朗日松弛方法是一种有效的求解复杂数学规划问题的方法, 主要有两大特点: 第一, 将复杂约束加入到目标函数, 减少求解过程中的约束判断; 第二, 尽量松弛掉偶合约束, 将不可分的复杂问题转化为可拆分的多个简单子问题。Ni等(2011)[173]提出了用于WTA的拉格朗日松弛方法。该方法首先引入离散变量, 将非线性整数规划问题转化为线性优化问题, 目标函数和原始变量是线性的, 引入的变量是非线性的, 然后构造了一个拉格朗日松弛问题, 并分解为两个子问题: 一个与引入的离散变量有关的非线性优化问题, 另一个与原始变量有关的线性问题。前一个问题可以分解为一维离散优化问题, 并易于并行处理, 后一个问题易于用单纯形法求解, 每个子问题根据各自的特点易于求解到最优解。然后利用这两个子问题的最优解更新拉格朗日乘子, 迭代求解拉格朗日松弛问题。该方法能快速找到较好的初始可行解, 并对其进行改进。
3.2.5 其他近似算法
除了上述算法外, 还有很多近似优化算法也探索了在WTA领域的应用。Chang等(1987)[106]提出了求解SWTA问题的迭代线性网络规划算法, 该算法结合了MMR算法和非线性网络流算法的特点, 对原非线性问题进行线性近似, 并通过组合线性网络流算法的迭代解, 获得接近最优的解。此外, 还开发了一种开环反馈算法来解决DWTA问题, 该算法的关键要素是结合最小边际增益阈值迭代使用SWTA算法来分配拦截器。Kolitz (1988)[174]假设不同武器对同一目标毁伤概率的相互独立性, 实现了一种非精确式的MMR算法求解WTA问题。Wacholder(1989)[8]和Gelenbe等(2010)[175]设计了一种基于神经网络的算法求解WTA问题, 前者由求解一个常微分方程组组成, 该方程组的轨迹是问题的赋值变量, 算法的主要优点是可以在快速模拟电路中实现; 后者基于随机神经网络的参数选择, 对网络进行均衡求解, 然后通过选择活跃概率最高的神经元来识别分配。
Bogdanowicz等(2013)[176]提出了一种基于期望杀伤概率的武器分配优化算法, 所提出的优化算法可以将武器分配给满足期望的杀伤概率和最小化过度杀伤的目标。Severson等(2015)[14]实现了一种分布式的、基于共识的方法来优化WTA领域的雷达资源管理。Bogdanowicz等(2015)[177]设计了一个基于枚举所有可能的武器-资产组合的创新算法, 以快速评估预先设定的WTA可能对中立/友好资产的附带伤害。Naseem等(2017)[178]提出了一种基于三维稳定婚姻算法的威胁评估和武器分配的新方法, 该方法主要包括三阶段: 威胁感知、威胁评估和威胁分配, 三维多对多稳定婚姻算法在后两个阶段发挥威胁配对作用。Davis等(2017)[16]和Summers等(2020)[103]利用近似动态规划方法求解WTA问题, 经典的动态规划算法, 如求解贝尔曼方程的策略迭代和值迭代, 完全依赖于状态空间的枚举, 无法处理维数灾难问题, 近似动态规划算法提供了一组可供选择的解决方案策略, 是解决维数爆炸的方法之一。Zhao等(2019)[179]重新设计了一种基于拍卖的算法和一种改进的任务交换算法以及两者的混合算法, 应用于蜂群作战WTA求解中。在直觉模糊多属性决策环境下, Gao等(2020)[180]提出了一种新的基于三向决策的目标威胁评估方法, 其核心部分是用直觉模糊TOPSIS(technique for order preference by similarity to an ideal solution)法估计各目标的条件概率, 并用直觉模糊评价值构造各目标的决策阈值。Hu等(2020)[181]设计了一种新的基于交叉熵的DWTA算法。
4 实验
在WTA问题发展的半个多世纪以来, 研究人员提出的算法在多大规模上有效、测试用例如何生成、有哪些公开测试集可用等问题, 是WTA模型和算法实验的研究重点。本节重点梳理了当前文献中实验部分的实验规模和数据来源, 为WTA的测试与实验提供参考。
4.1 实验规模
从当前文献的实验规模来看, 武器和目标的数量区间涵盖5个武器5个目标(5W*5T)的实验到400个武器400个目标(400W*400T)的实验。这里将(20W*20T)以下的称为小规模实验, (20W*20T)至(100W*100T)之间的为中等规模实验, (100W*100T)以上的为大规模实验。不同实验规模的代表性文献如表 4所示。

精确算法更加关注于求解小规模、静态的WTA案例。对于中大规模问题, 高维度的解空间使得列生成算法、枚举算法、分支定界算法等传统精确求解技术难以满足快速求解的需求, 而启发式算法可以在满足时效性的情况下求得较优的满意解。在一些应用智能算法的研究中, 经常使用小规模的测试集作为基准实验, 方便同精确算法比较, 验证所开发算法的可行性和有效性。在此基础上进行较大规模实验以验证算法的适用性, 如Cao等(2018)[152]、Ahner等(2015)[101]、Rezende等(2018)[153]、Wang等(2018)[155]。Sahin等(2014)[109]使用很小规模的实验去测试基于网格划分的模糊决策方法的有效性, 再测试中等规模(20W*40T)案例中的表现。
一般而言, 智能算法能够在可接受的时间里求解中大规模(100W*100T)以上WTA问题, 即可认为该算法在搜索效率上具有较好的性能。Bogdanowicz等(2015)[177]引入了一个并行和分布式处理结合的优化框架, 可以在短时间内找到(120W*120T)以内WTA问题的满意解。Sonuc等(2017)[128]等应用不同维度的12个测试案例(200W*200T以内)测试了并行SA算法的有效性。Xin等(2010)[129]设计了一个局部搜索算子, 并将其整合到禁忌搜索算法用于解决DWTA问题, 求解了超过(200W*200T)以上规模的案例。Cao等(2018)[152]开发出一个基于Spark框架的ACO算法, 能够在数十秒内找到3层防御武器、20个保护资产以及3种类型攻击性武器的满意WTA方案。实验结果表明, 分布式实验环境适用于大规模迭代启发式计算。
近些年, 多目标WTA问题逐渐成为WTA领域研究的一个重点, Liu等(2013)[182]、Zhou等(2016)[183]、Gu等(2015)[184]、Peng等(2017)[44]以及Li等(2018)[71]针对不同作战类型的WTA问题, 建立了对目标毁伤概率最大和武器或火力单元使用数量最小的双优化目标模型。实验以小规模案例为主, 仅Li等(2018)[71]求解了(90W*80T)以内的中等规模案例。Zhao等(2020)[185]求解了以最小化敌方总威胁度和最大化目标毁伤概率为目标的小规模问题。Li等(2018)[71]研究了一个三目标的WTA问题, 优化目标分别是最大化毁伤效率、最小化武器成本以及最大化战斗机整体作战价值, 求解规模仍以小规模为主。
4.2 测试数据
WTA模型算法的测试数据主要包括两类: 想定数据和随机数据。想定数据是论文作者依据实际装备和目标情况设计的数据, 一般会在文献中直接给出相对具体的武器和目标类型, 以及毁伤、收益等相关参数的具体取值, 如Li等(2018)[71]、Wang(2008)[150]等。也有相当一部分文献的测试数据采用随机方式生成, 并给出随机生成的方法。其中, 少数文献公布了随机测试数据集及其下载地址, 并逐渐被后续学者采用, 如Sonuc等(2017)[128]。表 5给出了测试数据的代表性文献及其获取方式, 其中想定数据可以通过查阅作者论文得到。表 5中的随机数据部分, 作者单独生成了随机数据集并公布了获取链接。

5 结束语
从20世纪五六十年代WTA问题开始发展, 先后经历了多个发展阶段, 相关研究逐渐呈现出多样化和深化发展状态。WTA问题从最初的弹道导弹防御领域扩展到了陆海空天电等各个作战领域, 支撑的作战样式从地面防空、舰艇防空、空中拦截等典型防御作战样式到对地打击、反舰、反卫星、装甲对战、联合火力打击等典型进攻样式。WTA的建模方法也从整数、混合整数等数学规划建模方法, 扩展到博弈论、图论、动态规划、多智能体、网络流等方法。由于WTA的NP-Hard特性, 求解算法一直是该领域的研究重点, 国内外学者尝试用各种精确算法和智能优化算法来求解WTA问题, 近年来开始探索机器学习算法在该领域的应用。总的来看, WTA问题属于指挥控制和任务规划领域的基础问题和难点问题, 尽管经过多年发展, 取得了丰富的研究成果, 当前的研究也存在以下不足。
随着智能化、无人化战争的发展, 无人集群目标、跨域打击等新的问题亟需解决。同时, 作战节奏的加快, 也需要进一步研究更快更好的求解算法。未来武器目标分配领域主要有如下几个重点发展方向:
-
(1) 随着无人装备的广泛应用, 可用武器的打击方式更加多样, 新的目标毁伤特点不断出现, 根据新的问题特点, 建立适合各种无人作战或有人无人协同作战的WTA模型。传统装备、建筑等点目标以及机场跑道等面目标的毁伤特点与新出现的无人机蜂群等空间集群目标具有很大差别。对于无人机集群这类空间集群目标, 当采用集群对抗时, 我方集群对敌方集群一般需要分布式打击方式, 将计算机智能体与分布式决策相结合是应对无人机蜂群以及低慢小无人系统等目标的重要方法。当采用范围杀伤武器时, 需要在无人机集群所在立体空域选择导弹起爆点, 而不再是每一架无人机, WTA一般需要转化为空间覆盖选址问题。
-
(2) 考虑WTA中的各种不确定因素的影响。当前研究大多关注确定环境下的WTA问题, 而实际作战中, WTA面临多种不确定因素的影响。一方面是可用武器资源的不确定性, 包括部分可用武器资源由于被打击、自身故障、临时征用等原因变得不再可用, 或者武器虽然可用, 但是毁伤概率、可用时段或数量等发生了变化。另一方面是目标的不确定性, 包括部分目标的突现、消失、打击时机变化等。同时, 两方面不确定因素的交互作用, 进一步给WTA带来了更多挑战。因此, 根据作战样式特点, 结合各种不确定因素影响, 研究更加贴近实战需求的WTA方法是未来该领域的重要发展方向之一。
-
(3) 在求解算法方面, 各种优化算法虽然已经研究了很多, 随着人工智能技术的发展, 研究线下深度学习、线上快速优化相结合的智能算法, 提高武器目标的时效性。同时, 针对不同作战样式的特点, 研究数据、知识和模型混合驱动的WTA算法, 也是提升典型作战样式分配效果的重要途径。此外, 构建WTA的算法库, 设计算法的智能推荐方法, 开发问题-算法的匹配与调用平台, 更好地满足指挥员决策偏好, 辅助生成更适合的无目标分配方案。
-
(4) 构建典型武器和典型目标的测试数据集。当前WTA方法的验证大多采用随机数据, 一定程度上验证了算法的有效性, 尚缺乏统一权威的测试数据集。根据典型作战样式特点以及武器目标毁伤规律, 构建可信、公开、通用的测试数据集, 为各类算法的验证、对比实验等提供参考, 是提升WTA算法有效性的重要基础。
本文仅用于学习交流,如有侵权,请联系删除 !!
加 V “人工智能技术与咨询” 了解更多资讯 !!