一个内径和外径分别为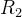 和
和 的导体球壳,带电荷
的导体球壳,带电荷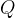 ,同心地包围着一个
,同心地包围着一个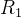 的导体球
的导体球 ,使这个导体球接地,求空间各点的电势和这个导体球的感应电荷
,使这个导体球接地,求空间各点的电势和这个导体球的感应电荷

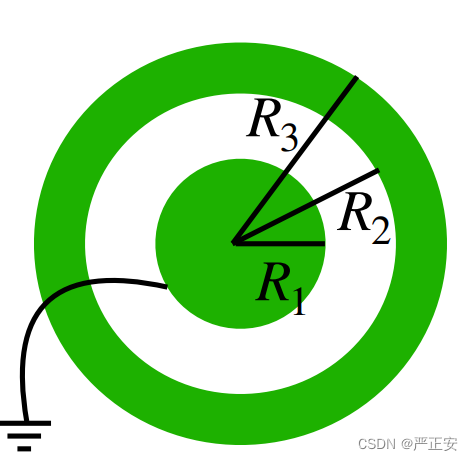
我们不难发现,球对称性非常强,电势只和半径有关系
所以我们可以假设电势为
我们假设
下面写出四个边界条件
导体表面带电量为
因为导体球壳表面电量的计算公式是
我们不难得到
我们可以得到
我们可以解得
电容率为 的介质球置于均匀外电场
的介质球置于均匀外电场 中,求电势
中,求电势

表示球外电势,
表示球内电势
(1)在无穷远处
因而
(2) 在处,
应该为有限值,因此
(3)在介质球面上:
比较系数,即可求得方程的解
总结一下可以发现
泊松方程和拉普拉斯方程的核心都在于如何寻找边界条件
在这些题目中,利用球坐标系的公式进行展开,利用对称性
牺牲掉部分精度,来换取一个比较容易的求解
是一个很值得参考的方法