前言:我们熟悉一维数组的前缀和和差分数组的相关操作和原理,但是对于二维数组也就是矩阵来说,它的差分和前缀和又会有什么不同之处呢?下面我们一起来研究,

1.二维数组的前缀和
首先,我们一般规定二维数组的前缀和为由坐标(1,1)到(i,j)所围成的矩形的区域中的所有元素的总和。
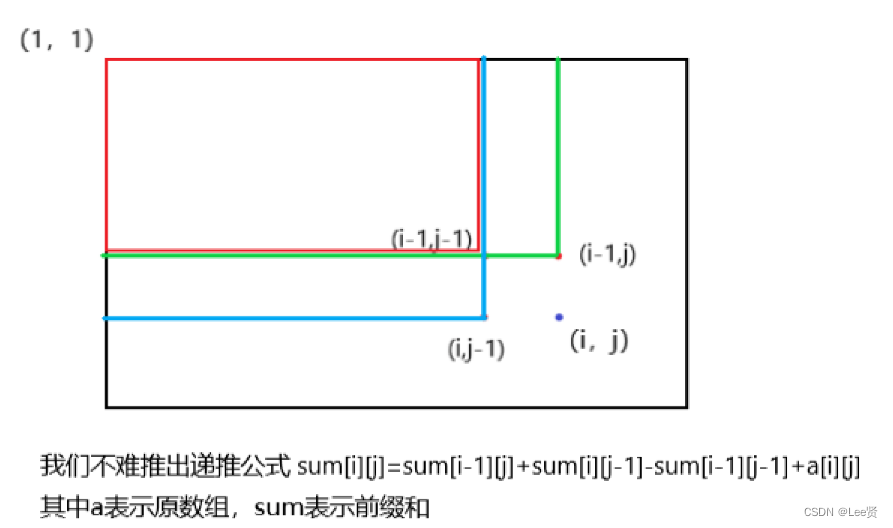
我们的重点就是落在如何求子矩阵的前缀和,这是一般的题目要考察的,我们下面来分析:
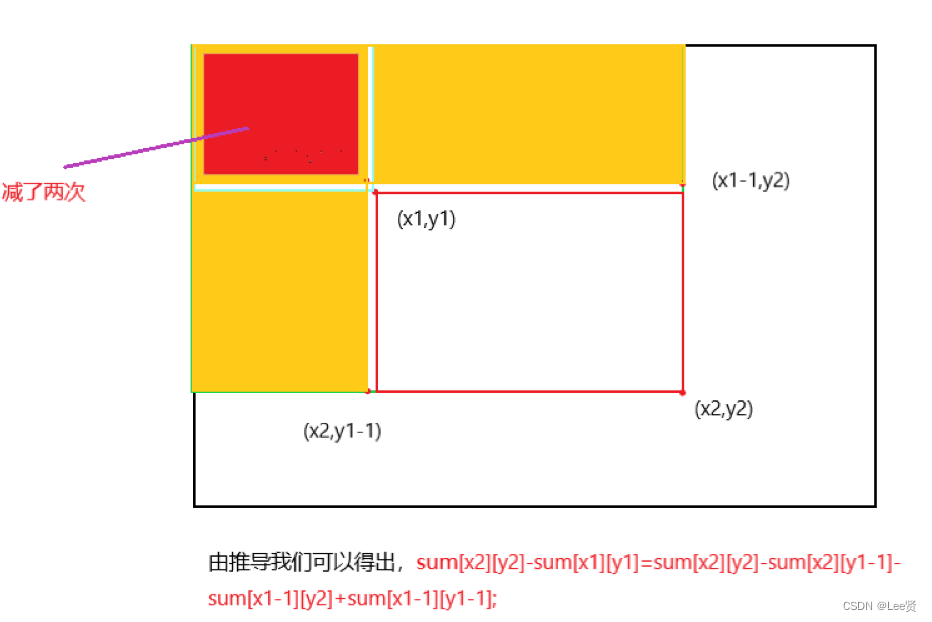
所以,经过以上分析,我们可以直接给出矩阵求前缀和和子矩阵和的参考代码:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, m,q;
int a[maxn][maxn], sum[maxn][maxn];
int main()
{scanf("%d%d%d", &n, &m,&q);for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++){scanf("%d", &a[i][j]);sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j];//(1,1)到(i,j)的前缀和}for (int i = 0; i < q; i++){int x1, y1, x2, y2;scanf("%d%d%d%d", &x1, &y1, &x2, &y2);printf("%d\n", sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]);}return 0;
}怎么样,是不是挺简单的?那么好,我们要上点难度了~~~
2.差分矩阵
这里我们需要知道前缀和与差分的关系:我们知道,通过差分数组可以求出原数组中每个元素的值,并且,我们可以发现,其实原数组就是差分数组的前缀和,这一点十分重要。
类比一下一维差分,一维差分是在一段上加上某个值,所以我们的二维差分就可以定义为将一个子矩阵的每个元素都加上某个数。
有了差分数组与原数组的关系,我们可以创建一个差分数组用于,这个数组性质就是可以像前面求前缀和一样求出原数组的每一个元素的值,而对于一个差分矩阵,我们对其中的某个元素加上一个值,影响的将是所有计算前缀和中包含该元素的部分,这点也十分重要,我们来用图说明一下,差分矩阵的效果:
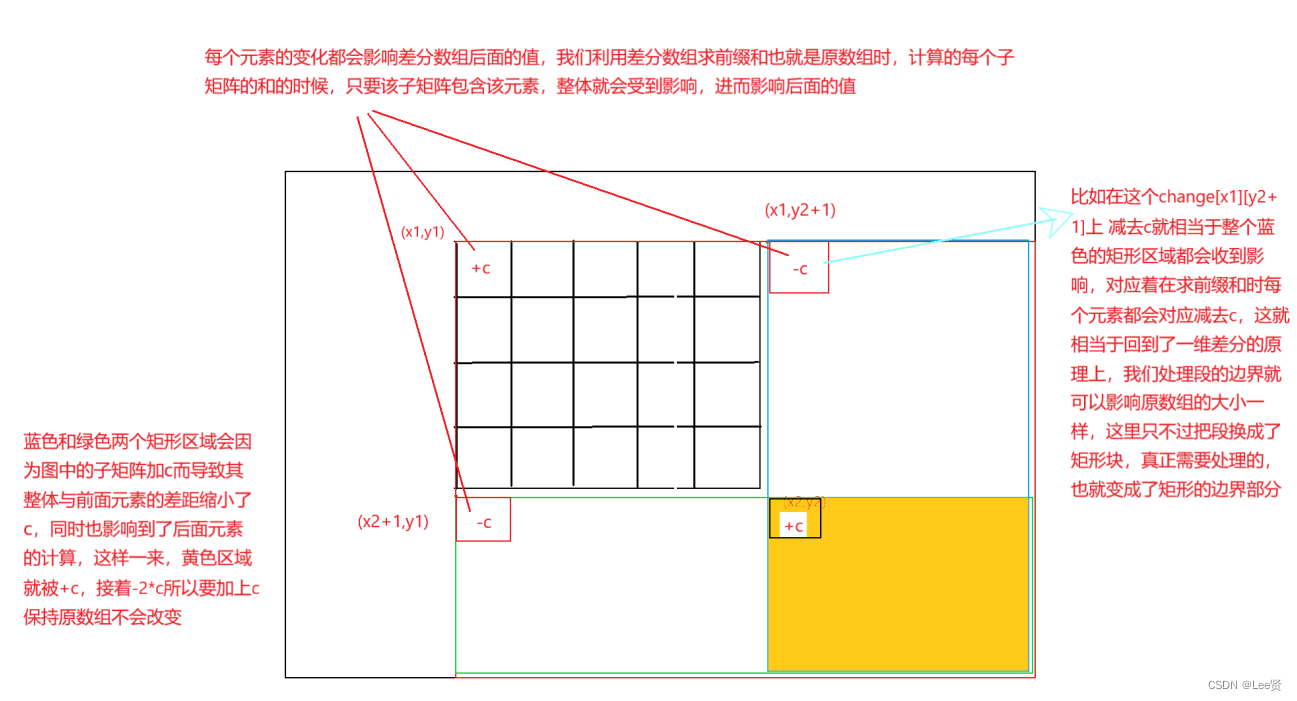
这一部分真的需要自己真正的理解,我自己深有体会,别人的理解毕竟很大程度上说不出来,
下面给出一道例题和代码进行理解:
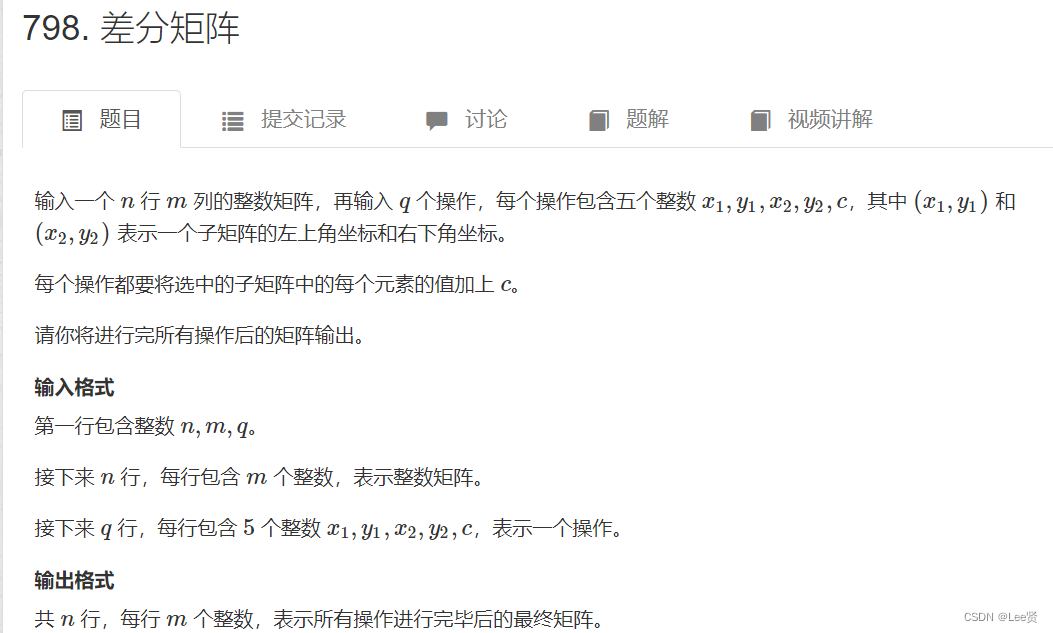

下面是代码:
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)//差分矩阵的核心
{b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}
int main()
{int n, m, q;cin >> n >> m >> q;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){insert(i, j, i, j, a[i][j]); //构建差分数组,这里相当于以一个只有一个元素的矩阵插入}}while (q--){int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);//受影响的边界将被改变}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //改变的边界进而影响二维前缀和即原数组,这里也体现了差分数组的前缀和就是原数组}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%d ", b[i][j]);}printf("\n");}return 0;
}