目录

一、知识图谱嵌入

二、transE算法

三、缺点

一、知识图谱嵌入

       知识图谱(Knowledge Graph，KG) 是大规模语义网络知识库，利用三元组（实体，关系，实体）来描述具体的知识，其具有语义丰富、结构友好、易于理解等优点。

       当今大规模知识库（知识图谱）的构建为许多自然语言处理任务提供了底层支持，例如问答系统、推荐系统等诸多领域，但由于其规模庞大且不完备，如何高效存储（低维稠密）[1]和补全知识库[2]成为了一项非常重要的任务，这就依托于知识表示学习（知识图谱嵌入技术）。

[1]计算机是无法直接处理自然语言的，自然语言中的词或知识必须将其编码成数字，计算机才能处理。稀疏编码能有效编码词汇信息，例如one-hot编码就是稀疏编码，词袋中[我，爱，苹果]三个字，对三个词进行编码，即“我”用[1，0，0]表示，“爱”用[0，1，0]表示，“苹果”用[0，0，1]表示，one-hot编码的优点就是直观有效地表示词汇，用向量中1位置表示该词在词袋中的位置。但其缺点就是随着词袋中词汇数量的增加，词汇向量表示的维度随之增加，当词袋中有一万个词时，词汇向量表示维度将达到一万，这种只用一个1，其余全是0的高维度稀疏编码必然造成编码繁琐、后期处理难度大。所以采用某种技术实现低维稠密编码，既降低了编码维度，也使得词与词之间存在关联，例如word2vec实现了关系相近的词在向量空间中离得近。同样，在知识图谱采用某种技术将实体、关系进行编码，同时保留两个实体间的关系，这种技术就是后文讲到的知识图谱嵌入（Knowledge Graph Embedding，KGE）。

[2]两个实体实际上有联系，但是在知识图谱中并未有直接边相连，如图1所示，例如[奥巴马]毕业于[哈弗大学]，但在知识图谱中，关系[毕业于]不存在，若在以此知识图谱为支撑的问答系统任务中，因为缺少关系，则会导致问答回复错误。所以需要某种技术补全知识图谱，这种技术就是知识图谱嵌入，编码后进行关系预测，即根据两个已知实体，预测该实体间的关系。

图1 实体间缺少关系

       表示学习旨在学习一系列低维稠密向量来表征语义信息，而知识表示学习是面向知识库中实体和关系的表示学习，将实体和关系投影到低维向量空间，实现实体和关系的语义信息表示。

二、transE算法

       知识图谱中的事实是用三元组 (头实体h , 关系r , 尾实体t )的结构组织的，那么如何用低维稠密向量来表示它们，才能得到这种依赖关系呢？

         transE算法就是一个非常经典的知识表示学习，其算法的思想非常简单，它受word2vec平移不变性的启发，关系的向量表示解释成头、尾实体向量之间的转移向量，如果一个三元组（h, r, t）为真，那么向量空间中对应向量需要符合h + r ≈ t，如图2、3所示。

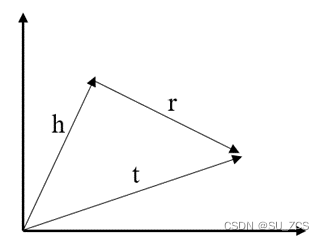
图2 实体-关系空间

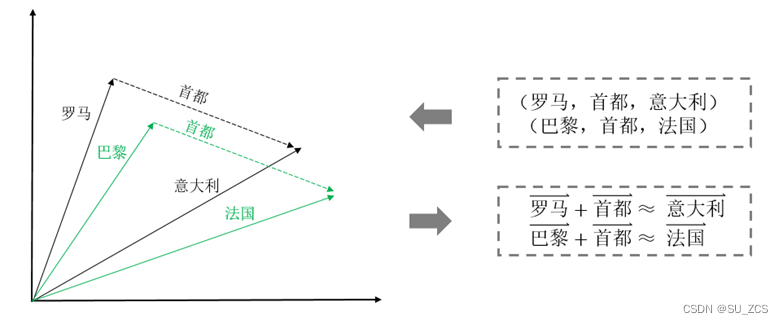
图3 平移距离示例

那如何进行学习（知识图谱嵌入）呢？

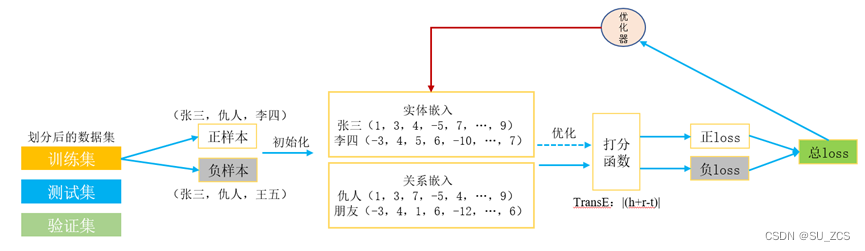
图3 知识图谱嵌入流程

       如图4所示，首先从训练集中抽取样本初始化样本的向量，然后基于距离的评分函数来对关系进行打分。

       如何设置打分模型损失函数是个关键，“表示学习”没有明显的监督信号，模型不会明确地告诉人们学到的表示正确与否，想要正确学习需要引入“相对”的概念，我们称正确的为正样本，错误的称为负样本，负样本是然后随机替换三元组的某个实体。相对负样本来说，正样本打分要更高。损失函数如下：

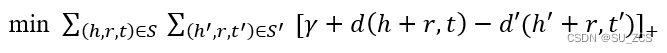
   （1）

S 表示正样本集

h,r,t 表示正样本的(头实体，关系，尾实体)

S’  表示负样本集

h’,r,t’ 表示负样本的(头实体，关系，尾实体)

Σ 表示求和公式

[ ]+ 表示max(0,x)，即当x大于0取x的值，当x小于0，取0。

γ 表示正负样本之间的间距，类似于支持向量机中的margin[3]。

d(x,y) 表示x，y向量的距离，这个距离可以是1范数，式（2）或2范数，式（3）。

（2）

 （3）

       这个损失函数很好理解，当正确三元组的距离越小，错误三元组的距离越大时，整体就会越接近0。

[3] 类似于支持向量机，这个方法也是线性分类，是将正样本和负样本点在空间中尽可能离得远，度量方法先画一条直线将两类点分开，并且使得这条直线距离两类点的间隔（Margin）最大。比如图4：（b）中直线A的margin，要比（c）中直线B的margin大，因此A直线要比B直线好很多。

图4 支持向量机的margin

举例：

这里实体有张三、李四、王五，关系有朋友，仇人，陌生人，其向量初始化为

张三（1，3，-5）
李四（-3，4，5）
王五（2，-1，3）
朋友（3，5，7）
仇人（-1，2，-1）
陌生人（2，-4，0）

有三对三元组（张三，朋友，李四）、（张三，仇人，王五）、（李四，陌生人，王五），向量表示为:

（（1，3，-5），（3，5，7），（-3，4，5））
（（1，3，-5）、（-1，2，-1）、（2，-1，3））
（（-3，4，5）、（2，-4，0）、（2，-1，3））

同时替换部分样本中的实体，（张三，朋友，王五）、（李四，仇人，王五）、（张三，陌生人，王五），以形成负样本，向量表示为：

（（1，3，-5），（3，5，7），（2，-1，3））
（（-3，4，5）、（-1，2，-1）、（2，-1，3））
（（1，3，-5）、（2，-4，0）、（2，-1，3））

进行损失计算，假设我们用2范数，

正样本：

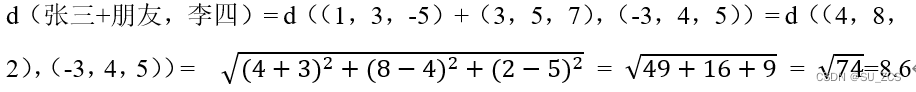
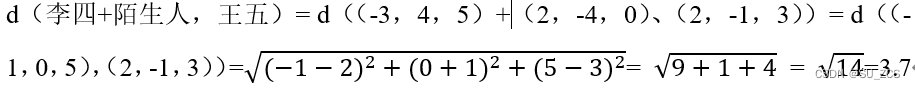
 负样本：

 

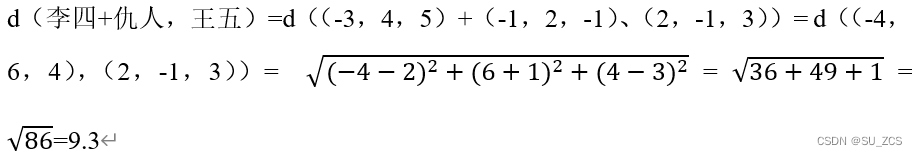
 设γ=2

通过梯度下降法更新之前随机生成的向量，最后最小化损失。

三、缺点

       不适合一对多、多对一、多对多，会出现冲突映射，一个实体在不同三元组内的表示融合，导致不明确甚至错误的语义信息。

举例：

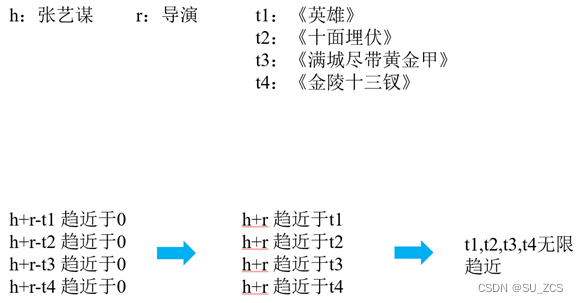
图5 transE不支持一对多示例

       如图5，h和r不变，h+r不变，当h+r分别趋向于t1、t2、t3、t4的时候，致使t1、t2、t3、t4无限接近，实际上四者分别独立。