2021年大连理工大学（开发区校区）Code人心弦初级组（正式赛）题解

难度预估

Easy：JFBH

Middle：AEKC

Hard：GDIL

实际效果

Easy：JFB

Middle：HC

Hard：KAEGD

？？？：LI

感想

思维题杀疯局

A题卡住的人有点多

题解

题解按原先设计的难度排序，

E和L两个题有出题人题解，

剩下的题解都是我（G题出题人）写的

J.搴檤（签到）

签到题，按题意累加求出第k项

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll k,f[1005];
int main(){scanf("%lld%lld%lld",&f[0],&f[1],&k);//if(k>40)while(1);assert(0<=f[0] && f[0]<=10);assert(0<=f[1] && f[1]<=10);assert(0<=k && k<=60);for(int i=2;i<=k;++i){f[i]=f[i-1]+f[i-2];}printf("%lld\n",f[k]);return 0;
}

F.小漳爱探险！（模拟）

最长回文串问题：

1. 复杂度O(n)的Manacher - OI Wiki

2. 复杂度O(n^2)的区间dp，dp[l][r]表示区间[l,r]是否是一个回文串

3. 复杂度O(n^2)的枚举回文中心，然后向两侧扩展，暴力判断

由于字符串是完全随机的，可以实际假设存在长为x的回文串，算一下出现长度为x的回文串概率，

发现实际出现很长的回文串的概率很小，实际随机的数据中，只有长度不超过15的回文串

因此，可以暴力从回文中心向两侧扩展，复杂度O(15*n)

需要注意需要循环两次，分别对应回文串长度为奇数/偶数的情形，

~~没看见写dp[i][20]的同学，倒是看见有抄manacher板子的同学，我的评价是寄~~

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10;
typedef pair<int,int> P;
int n,ans;
char s[N];
int main(){scanf("%d",&n);assert(1<=n && n<=1000000);scanf("%s",s+1);assert(strlen(s+1)==n);for(int i=1;i<=n;++i){assert(!(s[i]<'a' || s[i]>'z'));}for(int i=1;i<=n;++i){int l=i,r=i;while(l>=1 && r<=n && s[l]==s[r])l--,r++;ans=max(ans,r-l-1);}for(int i=2;i<=n;++i){int l=i-1,r=i;while(l>=1 && r<=n && s[l]==s[r])l--,r++;ans=max(ans,r-l-1);}printf("%d\n",ans);return 0;
}

B. lgl学图论（图论/最短路）

最短路 - OI Wiki板子题，用dijkstra跑1号点出发的单源最短路即可，

数据范围1e6，需要堆优化，注意图可能不连通

#include<bits/stdc++.h> 
using namespace std;
typedef pair<int,int> P;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,u,v,w,dis[N];
bool vis[N];
vector<P>e[N];
struct Q{int d,u;Q(){}Q(int dd,int uu):d(dd),u(uu){}
};
bool operator<(Q a,Q b){return a.d>b.d;
}
priority_queue<Q>q;
void dijkstra(int s){memset(dis,INF,sizeof dis);q.push(Q(0,s));dis[s]=0;while(!q.empty()){Q z=q.top();q.pop();int d=z.d,u=z.u;if(vis[u])continue;vis[u]=1;for(auto &x:e[u]){int v=x.first,w=x.second;if(dis[v]>dis[u]+w){dis[v]=dis[u]+w;q.push(Q(dis[v],v));}}}
}
signed main(){scanf("%d%d",&n,&m);assert(1<=n && n<=1000000);assert(1<=m && m<=1000000);for(int i=1;i<=m;++i){scanf("%d%d%d",&u,&v,&w);assert(1<=u && u<=n);assert(1<=v && v<=n);assert(1<=w && w<=1000);if(u==v)continue;e[u].push_back(P(v,w));e[v].push_back(P(u,w));}dijkstra(1);for(int i=1;i<=n;++i){printf("%d%c",dis[i]==INF?-1:dis[i]," \n"[i==n]);}return 0;
}

H.完全二叉树（树/先序遍历、中序遍历、完全二叉树判定）

题解做法及选手做法，基本是还原这棵二叉树+完全二叉树判定，

先递归建树，假设[l1,r1]是当前需要还原的先序区间，与之对应的中序区间为[l2,r2]

根据先序定义，l1一定是当前这棵树的根，在对应的中序区间内找到l1对应的位置，记为pos，

根据中序定义，中序区间[l2,pos)对应根的左子树，与其对应的先序区间为[l1+1,l1+pos-l2]；

(pos,r2]对应根的右子树，与其对应的先序区间为[r1-(r2-pos)+1,r1]，递归下去即可

完全二叉树判定：

1. 不存在一个点，有右子树，但没有左子树

2. 若按层（同层内先左后右）遍历这棵树，则：

i.若出现了一个点，只有左子树，没有右子树，则这个点之后的所有点，都是叶子节点

ii.若出现了一个叶子节点，则这个点之后的所有点，都是叶子节点

以上只要一条不满足，就不是完全二叉树

也可以采用标号的方式来判断：

设树当前点标号为i，则左儿子标号2*i，右儿子标号2*i+1，

设树节点为n，若不存在任一个点的标号大于n，即为完全二叉树

#include<bits/stdc++.h>
using namespace std;
const int N=30,M=26;
char pre[N],mid[N];
int n,m,cnt1[M],cnt2[M];
int rt,l[M],r[M];
bool lf[M];
int dfs(int l1,int r1,int l2,int r2){if(l1==r1){assert(l2==r2);assert(pre[l1]==mid[l2]);lf[pre[l1]-'A']=1;return mid[l2]-'A';}int pos=-1;for(int i=l2;i<=r2;++i){if(mid[i]==pre[l1]){pos=i;break;}}int ls=pos-l2,rs=r2-pos,v=pre[l1]-'A';if(ls)l[v]=dfs(l1+1,l1+ls,l2,pos-1);if(rs)r[v]=dfs(l1+ls+1,l1+ls+rs,pos+1,r2);return v;
}
bool bfs(){queue<int>q;q.push(rt);bool las=0;while(!q.empty()){int x=q.front();q.pop();if(las && !lf[x])return 0;if(r[x]!=-1 && l[x]==-1)return 0;if(l[x]!=-1 && r[x]==-1)las=1;if(l[x]!=-1)q.push(l[x]);if(r[x]!=-1)q.push(r[x]);}return 1;
}
int main(){memset(l,-1,sizeof l);memset(r,-1,sizeof r);scanf("%s%s",pre,mid);n=strlen(pre);m=strlen(mid);assert(n==m);assert(n<=26);for(int i=0;i<n;++i){assert('A'<=pre[i] && pre[i]<='Z');assert('A'<=mid[i] && mid[i]<='Z');cnt1[pre[i]-'A']++;cnt2[mid[i]-'A']++;}for(int i=0;i<26;++i){assert(cnt1[i]==cnt2[i]);}rt=dfs(0,n-1,0,n-1);puts(bfs()?"YE5":"N0");return 0;
}

当然也看到了选手的一个逆向做法，就是如果这棵树已经是完全二叉树，

先序访问[1,n]这n个点得到一个先序序列，中序访问[1,n]这n个点得到一个中序序列，

只需检查先序序列和中序序列相同点号的位置，在给定的输入中的字母是否完全一致即可

#include <bits/stdc++.h>
using namespace std;string s1,s2;
int len;
int cnt;
int a[100];
int first[100],mid[100];
int m1[100];//f字母->数字
int m2[100];//m字母->数字
int ls(int num){return num<<1;}
int rs(int num){return (num<<1)|1;}
void fDFS(int now){//cout << now << ' ' << dep << endl;first[++cnt]=now;if(ls(now)<=len)fDFS(ls(now));if(rs(now)<=len)fDFS(rs(now));
}
void mDFS(int now){if(ls(now)<=len)mDFS(ls(now));mid[++cnt]=now;if(rs(now)<=len)mDFS(rs(now));
}
int main(){//freopen("1.in","r",stdin);cin>>s1>>s2;len=s1.length();for(int i=1;i<=len;i++)a[i]=i;cnt=0;fDFS(1);cnt=0;mDFS(1);/*for(int i=1;i<=len;i++)cout << first[i] << ' ';cout << endl;for(int i=1;i<=len;i++)cout << mid[i] << ' ';cout << endl;*/for(int i=1;i<=len;i++)m1[s1[i-1]-'A']=first[i];for(int i=1;i<=len;i++){m2[s2[i-1]-'A']=mid[i];}/*cout << endl;for(int i=1;i<=len;i++)cout << m1[i] << ' ';cout << endl;for(int i=1;i<=len;i++)cout << m2[i] << ' ';cout << endl;*/for(int i=0;i<26;i++)if(m1[i]!=m2[i]){cout << "N0" << endl;return 0;}cout << "YE5" << endl;return 0;
}

A.火（多源bfs）

出题人刻意卡掉了堆优化dijkstra，可以说是很阴间了~~（怎么可能放两道dijkstra裸题呢）~~

正解是多源bfs，可以发现最短路的最大值不超过3000，所以可以开3000个队列，

增序遍历队列，对队列内的点更新距离，这其实就是分层图的思想

实际队列是可以被循环使用的，开 $max_{w}+1$ 个就够了，其中 $max_{w}$ 为最大边权，这里为5

因为5比较小，也可以将格子拆成5个点，第i个点连第i+1个点，边权为1，

第5个点连四邻的0号点，边权为1，对新图直接跑bfs

顺便一提，循环这个奇技淫巧，codeforces有篇博客，管它叫1-k bfs

#include<bits/stdc++.h>
using namespace std;int n,a[310][310],k,ans,x,y;
vector<pair<int,int> > v[3010];
char s[310];int main()
{scanf("%d",&n);assert(1<=n && n<=300);for (int i=1; i<=n; i++){scanf("%s",s+1);assert(strlen(s+1)==n);for (int j=1; j<=n; j++) a[i][j]=s[j]-'0',assert(1<=a[i][j] && a[i][j]<=5);}scanf("%d",&k);assert(1<=k && k<=50);for (int i=1; i<=k; i++) scanf("%d%d",&x,&y),assert(1<=x && x<=n),assert(1<=y && y<=n),assert(a[x][y]),v[a[x][y]].push_back(make_pair(x,y)),a[x][y]=0;for (int i=1; i<=3005; i++)for (int j=0,sz=v[i].size(); j<sz; j++){ans=i;x=v[i][j].first,y=v[i][j].second;if (x>1&&a[x-1][y]) v[i+a[x-1][y]].push_back(make_pair(x-1,y)),a[x-1][y]=0;if (y>1&&a[x][y-1]) v[i+a[x][y-1]].push_back(make_pair(x,y-1)),a[x][y-1]=0;if (x<n&&a[x+1][y]) v[i+a[x+1][y]].push_back(make_pair(x+1,y)),a[x+1][y]=0;if (y<n&&a[x][y+1]) v[i+a[x][y+1]].push_back(make_pair(x,y+1)),a[x][y+1]=0;}printf("%d\n",ans);return 0;
}

E.棋盘染色（思维题）

对于n>=2，m>=2的情形，由于受损格子两两之间不是八连通相邻的，

所以非受损格子一定是一个连通块，每一个格子都需要染色，黑白染色只有两种方案，

即对于第i行第j列(1<=i<=n,1<=j<=m)，i+j为奇数的染成一种颜色，为偶数的染成另一种颜色

讨论(1,1)分别被染成黑色或白色，保留更优的那一种

对于n=1或m=1的情形，一个受损的格子就可以把格子条分割为互不影响的两部分，

若干个受损格子将格子条分割为若干段，对每一段贪心，保留黑色更多的即可

出题人题解

可以发现，在大部分情况下，合法的染色方案只有两种。

即对于坐标为 $(x,y)$ 的格子， $x+y$ 为奇数的染一种颜色，为偶数的染另一种颜色。

因此只要统计两种奇偶性的格子的总数：为奇数的总共有 $\left \lfloor \frac {n\times m} 2 \right \rfloor$ 个，为偶数的总共有 $\left \lceil \frac {n\times m} 2\right \rceil$ 个，再分别减去对应的受损格子的数量，取较多的那类涂黑即可。

在特殊的 $n=1$ 或 $m=1$ 的情形，这种时候受损格子会将整个棋盘分成若干个独立的段，可以发现每段最开始涂黑一定是最优的，所以 $(1,1)$ 一定是黑色。同时，一个有 $tot$ 个格子的连续段最多能凃出 $\left \lceil \frac{tot}2 \right \rceil$ $个黑色格子。因此只要将受损格子从小到大排序后根据每段长度计算黑色格子总数即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,k,x[N],y[N],a[2],mn=INF;
bool swp;
void out(ll x,bool b){printf("%lld\n%s",x,b?"Black":"White");
}
int main(){scanf("%d%d%d",&n,&m,&k);assert(1<=n && n<=1000000000);assert(1<=m && m<=1000000000);assert(1<=k && k<=1000000);if(n>m)swap(n,m),swp=1;for(int i=1;i<=k;++i){scanf("%d%d",&x[i],&y[i]);if(swp)swap(x[i],y[i]);a[(x[i]+y[i])&1]++;}if(n==1){sort(y+1,y+k+1);y[k+1]=m+1;int ans=0;for(int i=1;i<=k+1;++i){int v=y[i]-y[i-1]-1;ans+=(v+1)/2;}out(ans,1);return 0;}ll u=1ll*n*m/2,v=1ll*n*m-u;if(v-a[0]>=u-a[1])out(v-a[0],1);else out(u-a[1],0);return 0;
}

K.黑白棋（思维题）

首先，对于同一行/列取反翻转两次是会被抵消的，

仔细观察可以被恢复成全1的矩阵，可以发现，

11101010

00010101

11101010

只考虑行操作的翻转时，第一行只能是11101010或00010101，

那么，第二行也只能在翻转后是11101010或00010101，也即翻转前11101010或00010101，

反证法，若第二行不为11101010或00010101，且能翻转成全1矩阵，

则必有一位和第一行不同，记为第x位，

此后在进行列的翻转时，会同时改变第一行第x位和第二行第x位，

使二者仍不同，与能翻转成全1矩阵矛盾

因此，后面的行与前面的行相比，只能要么完全相同，要么完全相反

逐字符比对、字符串判等、哈希、bitset均可，这里给出一种实现

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const int N=1e5+10;
string x,y;
int n,m,v,cnt;
int main(){cin>>n>>m;assert(1<=n && n<=2000);assert(1<=m && m<=2000);for(int j=1;j<=m;++j){cin>>v;cnt+=(v==1);assert(0<=v && v<=1);x+=v+'0';y+='1'-v;}int cnt2=1;for(int i=2;i<=n;++i){string now;for(int j=1;j<=m;++j){cin>>v;assert(0<=v && v<=1);now+=v+'0';}if(now!=x && now!=y){cout<<-1<<endl;return 0;}cnt2+=(now[0]==x[0]);}cout<<min(m+n-cnt-cnt2,cnt+cnt2)<<endl;return 0;
}

当然，也看到了一个选手提交的很精彩的判合法的方式，

for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&f[i][j]);if(i>=2&&i<=n&&j>=2&&j<=m){int t=f[i][j]+f[i-1][j]+f[i-1][j-1]+f[i][j-1];if(!(t==2||t==0||t==4)){flag=0;}}}
}

即每个2*2的方格内数字之和只能是0或2或4，不难证明二者是等价的

C. 颜料（并查集）

题解做法及AC做法中的非暴力做法都是并查集做法，这里给出一种实现，

col[i]表示颜色为i的最左节点是哪个节点，

par[i]表示和i当前颜色相同的最左节点是哪个，

now[i]表示i这个位置的当前颜色是什么

插入：新建一个位置c，分是否第一次出现该颜色讨论，更新对应的数组

合并：忽略当前颜色相同的情况，忽略x颜色不存在的情况，否则，

找到x颜色的最左位置cx，找到y颜色的最左位置cy，把cx这条链往cy这条链上挂，

类似链表合并，但是用并查集，只对两个链头操作，更新对应的数组

查询：找到当前位置所在链的最左位置，查其颜色即可

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,op,x,y,c;
int col[N],par[N],now[N];//col[i]:颜色为i的第一个节点是哪个节点 par[i]:和i当前颜色相同的最前的节点是哪个节点
int find(int x){return par[x]==x?x:par[x]=find(par[x]);
}
int main(){scanf("%d",&n);assert(1<=n && n<=1000000);for(int i=1;i<N;++i){par[i]=i;}for(int i=1;i<=n;++i){scanf("%d",&op);assert(1<=op && op<=3);if(op==1){scanf("%d",&x);assert(1<=x && x<=1000000);++c;if(!col[x])col[x]=c,par[c]=c,now[c]=x;else par[c]=find(col[x]);}else if(op==2){scanf("%d%d",&x,&y);assert(1<=x && x<=1000000);assert(1<=y && y<=1000000);int cx=col[x],cy=col[y];if(!cx)continue;if(!cy)cy=cx;col[x]=0;int mx=max(cx,cy),mn=min(cx,cy);par[mx]=mn;col[y]=mn;now[mn]=y;}else{scanf("%d",&x);assert(1<=x && x<=1000000);y=find(x);printf("%d\n",now[y]);}}return 0;
}

G.懒兔n窟（树/树的遍历+双指针）

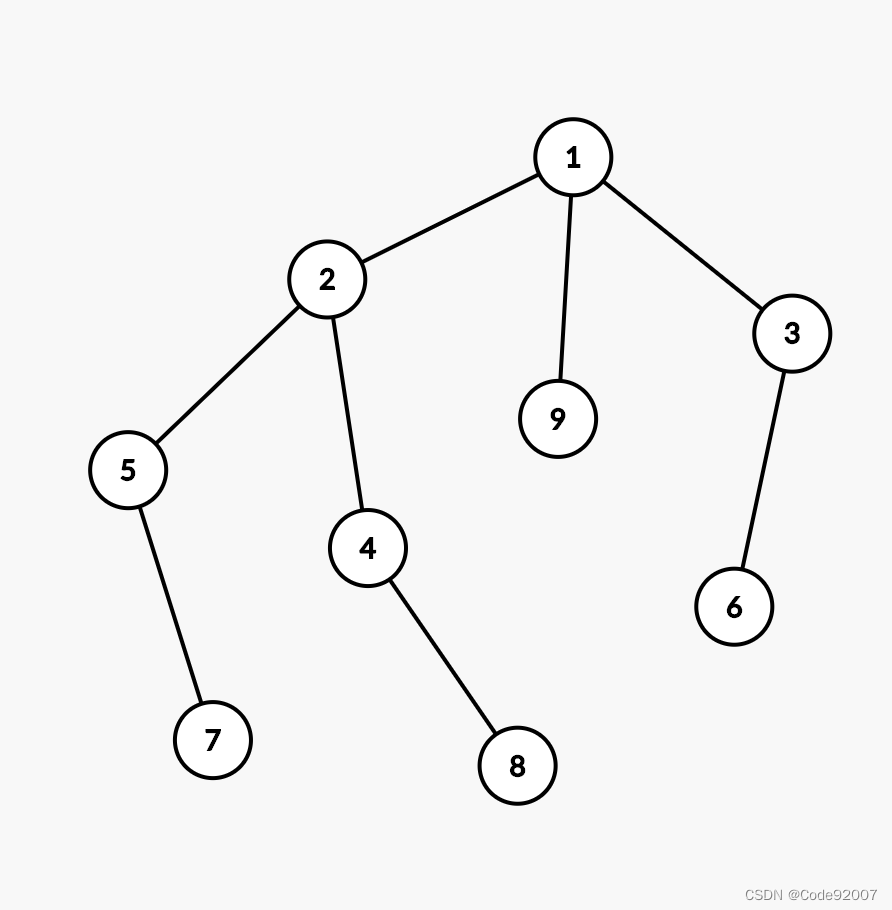
划水兔加边前是一棵树，不妨划水兔加边连接5-3，得到一棵基环树。

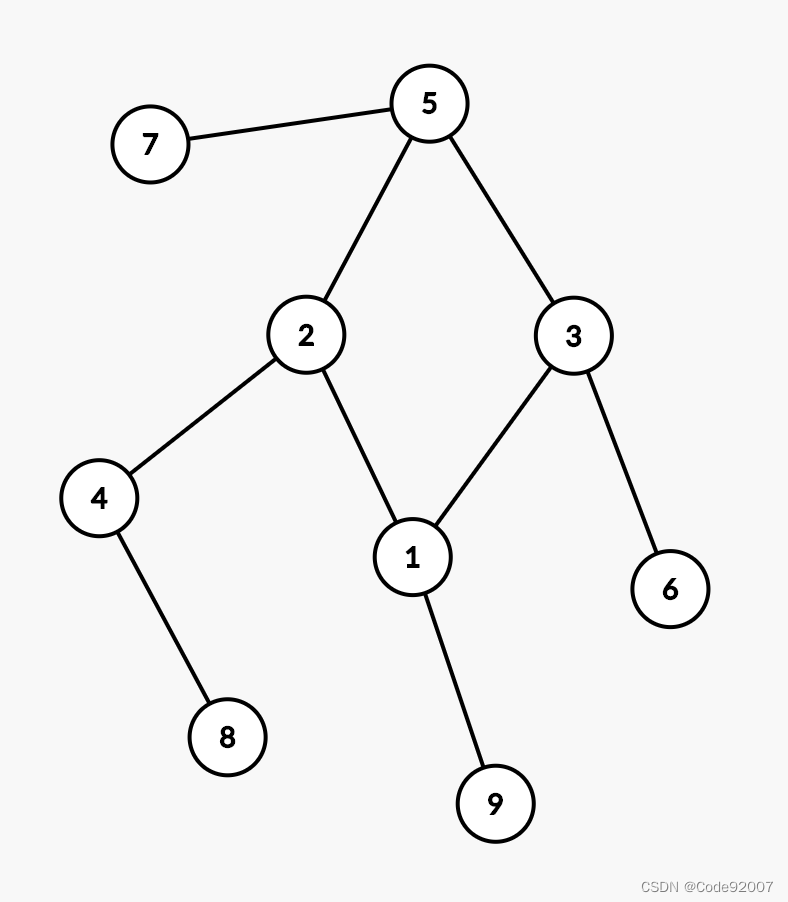
因为不在环上的边没有发生改变，所以若(u,v)的最短路变短，(u,v)必经至少一条环上边

换言之，u想要去v，必然先要走到离它最近的环上点x，再从x选两条路径中的一条去v

这表明，u的贡献是可以被放在环上点x下考虑的，也即：

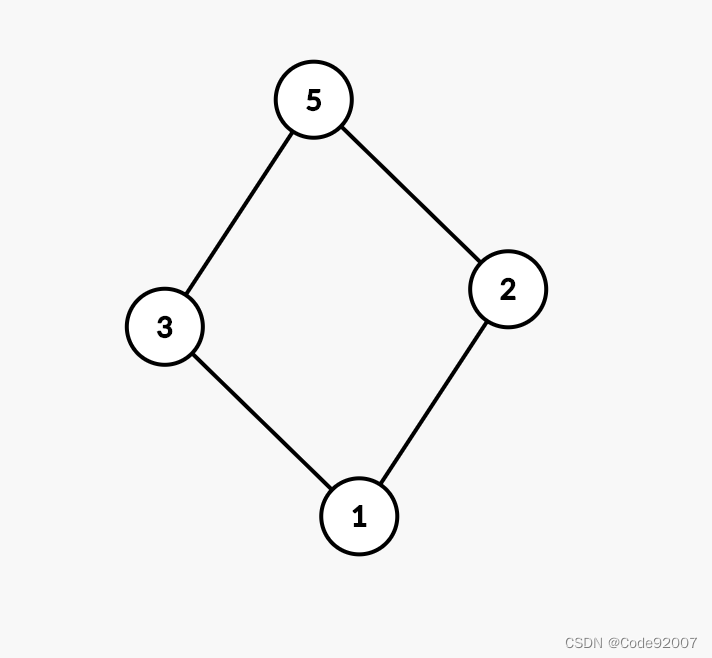
实际5代表了5、7两个点，以此类推，

所以，先断开环上边，得到森林，

对每个环上点为根dfs，将得到的连通块的大小，作为其实际代表的点的个数，

就退化成了一个双指针问题，拆掉5-3这条边，环退化成一条链，

枚举每个点u，与之能产生贡献的v是所有这条链上距离超过环长一半的点，

注意需要分环长为奇/偶讨论

//#pragma comment(linker, "/STACK:102400000,102400000") 
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
typedef long long ll;
const int N=1e6+10;
bool ban[N];
vector<P>e[N];
vector<int>rt,rt2;
int n,u,v,par[N],parE[N],dep[N],sz[N];
void dfs(int u,int fa,int id){par[u]=fa;dep[u]=dep[fa]+1;parE[u]=id;for(auto &x:e[u]){int v=x.first,id=x.second;if(v==fa)continue;dfs(v,u,id);}
}
void dfs2(int u,int fa){sz[u]=1;for(auto &x:e[u]){int v=x.first,id=x.second;if(v==fa || ban[id])continue;dfs2(v,u);sz[u]+=sz[v];}
}
ll solve(){int m=rt.size();if(m<=2)return 0;int now=m/2+1;ll ans=0,sum=0;for(int i=now;i<m;++i){sum+=sz[rt[i]];}for(int i=0;i<m && now<m;++i,++now){ans+=1ll*sz[rt[i]]*sum;sum-=sz[rt[now]];}return ans;
}
int main(){//freopen("16.in","r",stdin);//freopen("16.out","w",stdout);scanf("%d",&n);for(int i=1;i<n;++i){scanf("%d%d",&u,&v);e[u].push_back(P(v,i));e[v].push_back(P(u,i));}scanf("%d%d",&u,&v);dfs(1,0,0);while(u!=v){if(dep[u]>dep[v]){rt.push_back(u);ban[parE[u]]=1;u=par[u];}else{rt2.push_back(v);ban[parE[v]]=1;v=par[v];}}rt.push_back(u);for(int i=rt2.size()-1;i>=0;--i){rt.push_back(rt2[i]);}for(auto &u:rt){dfs2(u,0);}printf("%lld\n",2ll*solve());return 0;
}
/*
4   
1 2
2 3
3 4
1 3
*/

D.lgl学下棋（博弈/SG函数）

前置知识：SG函数（公平组合游戏 - OI Wiki）

首先，如果存在棋子初始位置就在（0，x）或（x，0）或（x，x），先手必胜，可以先判掉，

对于不存在的情形，两人一定不会把棋子往这些地方走，不然必输，

所以，可以看成是两个人在一张除去（0，x）（x，0）（x，x）的棋盘上玩博弈游戏，

可以发现这张新棋盘最小的两个位置是（1，2）、（2，1），均为先手必败位置，令其sg值为0，

用sg函数处理出每个坐标的值，总sg值为n个棋子sg值的异或，为0则先手必败，否则先手必胜

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e3+5;
int n,m,x,y,dp[N][N],sg;
bool vis[N][N];
int dfs(int x,int y){if(~dp[x][y])return dp[x][y];set<int>q;for(int i=1;i<x;++i){if(i!=y)q.insert(dfs(i,y));}for(int i=1;i<y;++i){if(i!=x)q.insert(dfs(x,i));}for(int i=1;i<min(x,y);++i){q.insert(dfs(x-i,y-i));}for(int i=0;;i++){if(!q.count(i)){return dp[x][y]=i;}}}
int main(){memset(dp,-1,sizeof dp);scanf("%d%d",&n,&m);assert(1<=n && n<=100);assert(1<=m && m<=100);dp[1][2]=dp[2][1]=0;//dp[1][1]=1;for(int i=1;i<=n;++i){scanf("%d%d",&x,&y);if(x==0 || y==0 || x==y){puts("YE5");return 0;}assert(0<=x && x<=m);assert(0<=y && y<=m);sg^=dfs(x,y);}puts(sg?"YE5":"N0");return 0;
}

I.TOC3公开赛（期望/概率dp）

dp[i][j]表示第i个卡组还有j张原来的卡没有被抽走的概率，每个卡组单独考虑对期望的贡献，

把卡组x的卡放到卡组y中z张时，新增贡献即为本次抽卡新增的dp[x][0]

枚举卡组x当前还有多少张原来的卡没被抽走，

枚举本次抽走了多少张卡组x原来的卡，进行转移

因为Q只有1000，所以可以读入所有询问离散化一下，只开2000*100的dp数组，

注意，一开始就没卡的卡组，视为所有卡均被阿玮抽到过，要一开始就加上贡献，

此外，抽卡组和重新分配组相同时不需要特判，因为卡会先被放到待定区，也视为阿玮抽卡了

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,Q=2e3+10,K=105,mod=1e9+7;
int n,q,a[N],b[Q],c;
int to[N],dp[Q][K],f[K],ans;//dp[i][j]:第i个卡组还有j张原来的卡没被抽走的概率
int Finv[N],fac[N],inv[N];
struct Query{int x,y,z;
}e[N];
int modpow(int x,int n,int mod){int res=1;for(;n;x=1ll*x*x%mod,n>>=1)if(n&1)res=1ll*res*x%mod;return res;
}
void init(int n){ //n<Ninv[1]=1;for(int i=2;i<=n;++i)inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;fac[0]=Finv[0]=1;for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%mod,Finv[i]=1ll*Finv[i-1]*inv[i]%mod;
}
int C(int n,int m){if(m<0||m>n)return 0;return 1ll*fac[n]*Finv[n-m]%mod*Finv[m]%mod;
}
int invC(int n,int m){if(m<0||m>n)return 1;return 1ll*fac[m]*fac[n-m]%mod*Finv[n]%mod;
}
void add(int &x,int y){x=(x+y)%mod;
}
int main(){init(N-5);scanf("%d%d",&n,&q);assert(1<=n && n<=100000);assert(1<=q && q<=1000);for(int i=1;i<=n;++i){scanf("%d",&a[i]);assert(0<=a[i] && a[i]<=100);}for(int i=1;i<=q;++i){scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z);assert(1<=e[i].x && e[i].x<=n);assert(1<=e[i].y && e[i].y<=n);assert(0<=e[i].z && e[i].z<=20);if(!to[e[i].x])to[e[i].x]=++c,b[c]=a[e[i].x];if(!to[e[i].y])to[e[i].y]=++c,b[c]=a[e[i].y];e[i].x=to[e[i].x];e[i].y=to[e[i].y];}for(int i=1;i<=n;++i){if(!a[i])add(ans,1);}for(int i=1;i<=c;++i){dp[i][b[i]]=1;}for(int i=1;i<=q;++i){memset(f,0,sizeof f);int from=e[i].x,to=e[i].y,dif=e[i].z;assert(dif<=b[from]);add(ans,mod-dp[from][0]);int up=min(b[from],100);for(int j=up;j>=0;--j){//当前剩j张原卡if(!dp[from][j])continue;for(int k=min(j,dif);k>=0;--k){//本次抽了k张原卡int prob=1ll*C(j,k)*C(b[from]-j,dif-k)%mod*invC(b[from],dif)%mod;add(f[j-k],1ll*dp[from][j]*prob%mod);}}memset(dp[from],0,sizeof dp[from]);b[from]-=dif;b[to]+=dif;for(int j=up;j>=0;--j){dp[from][j]=f[j];}add(ans,dp[from][0]);printf("%d\n",ans);/*printf("i:%d\n",i);for(int j=1;j<=c;++j){for(int k=0;k<=b[j];++k){printf("i:%d dp[%d][%d]:%d\n",i,j,k,dp[j][k]);}}*/}return 0;
}

L.分数（farey序列性质/二分+莫比乌斯反演）

该问题可见于2007年Yang Zhe的论文，一类分数问题的研究.pdf

题目给出的集合有序时得到的序列，被称为farey序列，第n个farey序列的第k项即为所求，

截图中给出的是求从小到大第k项，这里需要求从大到小第k项，方法类似，

~~我并没有想清楚这个f(i)预处理了什么东西，所以多了个log~~

先二分mid，检查答案时，

需要对每个分母i，求满足 $\frac{x}{i} \geq \frac{mid}{n*n},x \leq i, (x,i) == 1$ 的x的数量，

即 $[ceil(\frac{mid*i}{n*n}),i]$ 内与i互质的数的个数，

即 $\phi(i)$ 减去 $[1,ceil(\frac{mid*i}{n*n}))$ 内与i互质的个数，

不妨记 $ceil(\frac{mid*i}{n*n}))$ 为r+1，根据莫比乌斯反演e=mu*i，有

$\sum_{j=1}^{r}[gcd(i,j)==1] = \sum_{d|gcd(i,j)}\mu(d)\sum_{k=1}^{r/d}1=\sum_{d|gcd(i,j)}\mu(d)\left \lfloor \frac{r}{d} \right \rfloor$

注意到gcd(i,j)一定为i的因数，而j是枚举的，所以只需求：

$\sum_{d|i}\mu(d)\left \lfloor \frac{r}{d} \right \rfloor$

总复杂度 $O(n(logn)^2)$

出题人题解

写在前面：

其实原题是 $k\le 10^5$ 的，看到题后想出的做法发现和 $k$ 没有关系……

于是就加强了一下放了上来。

求第 $k$ 大和求第 $k$ 小只差一个 $|S|$ 的大小，而 $|S|=\sum\limits_{i=1}^n \varphi(i)$ ，线性筛出 $\varphi(i)$ 即可求出 $|S|$ ，

因此我们将问题转换为求第 $k$ 小的分数。

考虑二分答案对应的小数 $mid$ ，那么就是要计算 $|S|$ 中 $\le mid$ 的分数有多少个，

即统计 $\frac{p}{q}\le mid$ 且 $p,q$ 互质的 $(p,q)$ 数对个数，移项一下变成 $p\le mid\times q$ 。

先写出枚举的式子，然后考虑化简。

$\begin{aligned} ans&=\sum_{q=1}^n\sum_{p=1}^{\lfloor mid\times q\rfloor}[\gcd(p,q)=1]\\ &=\sum_{q=1}^n\sum_{p=1}^{\lfloor mid\times q\rfloor}\sum_{d|p,d|q}\mu(d)\\ &=\sum_{d=1}^n\mu (d)\sum_{q=1}^{\lfloor \frac n d\rfloor}\lfloor \frac{\lfloor mid\times q \times d \rfloor}d \rfloor \end{aligned}$

下取整是可以合并的，因此化为
$\begin{aligned} ans&=\sum_{d=1}^n\mu (d)\sum_{q=1}^{\lfloor \frac n d\rfloor}\lfloor mid\times q\rfloor \\ &=\sum_{i=1}^n \lfloor mid\times i\rfloor \sum_{d=1}^{\lfloor \frac n i \rfloor}\mu(d) \end{aligned}$

$\mu(d)$ 同样可以用线性筛求出来，然后再求个前缀和， $ans$ 就可以 $\Theta(n)$ 求出了。

因此二分完后可以 $\Theta(n)$ 判断，总的复杂度是 $\Theta(n\log n)$ 的。

求出答案对应的的小数数值 $val$ 后，我们只需要从 $1$ 到 $n$ 枚举分母 $q$ ，然后把 $val\times q$ 当做分子 $p$ ，判断一下 $\frac p q$ 是不是 $val$ 就可以找到 $val$ 对应的分数形式了。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
ll n,k;
int mu[N],phi[N],cnt;
vector<int>fac[N];
void sieve(){mu[1]=1;for(int i=1;i<N;++i){phi[i]=i;}for(int i=1;i<N;++i){fac[i].push_back(i);for(int j=2*i;j<N;j+=i){fac[j].push_back(i);mu[j]-=mu[i];phi[j]-=phi[i];}}
}
//[1,r]内与x互质的数的个数 r,x<=1e5
int cal(int r,int x){if(r<=0)return 0;int ans=0;for(auto &d:fac[x]){ans+=mu[d]*(r/d);}//printf("r:%d x:%d ans:%d\n",r,x,ans);return ans;
}
int main(){sieve();scanf("%lld%lld",&n,&k);ll l=1,r=n*n;while(l<=r){ll mid=(l+r)/2,cnt=0;for(int i=1;i<=n;++i){//x/i>=mid/(n*n)int r=1ll*(mid*i+n*n-1)/(n*n);//x>=ceil(mid*i/n*n);if(r==i)continue;int add=phi[i]-cal(r-1,i);//[r,i-1]内有多少数与i互质 //printf("mid:%lld i:%d r:%d add:%d\n",mid,i,r,add);cnt+=add;if(cnt>=k)break;}if(cnt>=k){l=mid+1;}else{r=mid-1;}}//r/(n*n) 最大的r 满足后缀和>=k x/i>=r/(n*n) int son=1,fa=1;for(int i=1;i<=n;++i){int x=1ll*(r*i+n*n-1)/(n*n);if(1ll*fa*x<1ll*son*i){son=x;fa=i;}	}printf("%d/%d\n",son,fa);return 0;
}

~~关于我看到题就想到是论文原题，但是想了半天没想出来O(nlogn)咋做，~~

~~而出题人想到了O(nlogn)做法，却根本就没看过这篇论文这件事~~

~~我在负一层啊~~