1.刚体的定轴转动

思考：改变转动状态的因素

答：改变刚体运动状态的的因素有力的大小及力臂有关，力与力臂的乘积为力矩。

力臂：力到转轴的距离

简而言之，改变刚体运动状态的因素是力矩，与力和力臂有关。

2.如何计算力矩

如图，图中d为力臂的大小，F为力的大小，则力矩M=Fd，而d又等于rsinθ（θ用中文输入法theta即可打出），r是从转轴的旋转点o到力的作用点的距离，称为径矢，所以力矩M=Frsinθ。上图中还有一种计算力矩的方法，为叉乘法，其中，力矩的向量=径矢的向量×力的向量（顺序一定一定不能乱！）可以这样子来理解：M代表母亲，r代表晾衣杆，F代表衣服，连起来就是一位母亲用晾衣杆晾衣服。这样就很方便记忆了。 

3.思考一个问题：当我们在骑自行车或者摩托车时，遇到紧急情况，我们如果快速刹车会发生什么情况，应该用前刹还是后刹呢？

我们先来分析自行车在刹车时的受力情况：

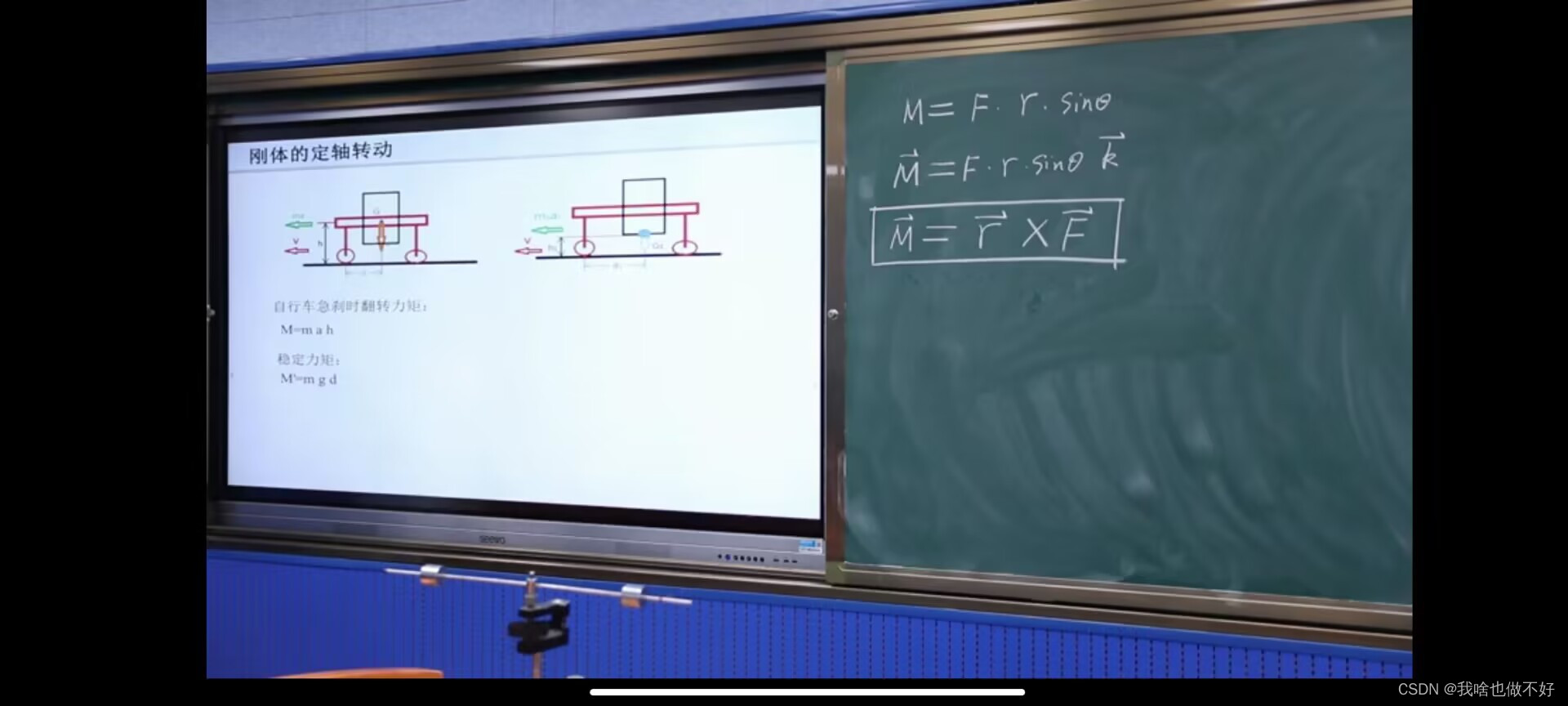
首先，自行车急刹车时，会向前方产生一个惯性力，大小为ma，这个力的力臂为h，这个力矩会使自行车有逆时针翻转的趋势，此外，自行车还受到重力，重力的力臂为d，重力产生的力矩会给自行车一个阻止翻转的趋势，与自行车的惯性力相反，因此，重力也被称为稳定力。因为自行车较轻，所以重心比较高，因此ma产生的位置也比较高，h比较大，所以mah>>mgd，因此，在急刹车时会产生翻转。

接着我们再来看摩托车的情况：

 

 因为摩托车比较重，且质量都集中在底部的油箱中，因此摩托车的重心特别低，所以h就比较小，当急刹车时，mah<<mgh，因此不会翻转，只会打滑。

 2.转动定律

 1.转动定律的推导

 由于转动情况下，只有切向的力能够影响物体的运动状态，所以这里只考虑切向的力，不考虑其他方向的力。

推导过程：

 

 可以把M=Ja类比成F=ma，其中，J为转动惯量，只与物体的m和r有关，a为物体的角加速度。

思考：如何让风车在风力大小不定的情况下发挥最高的性能？

 

 答：只需要在风力发电机内部安装一个可移动的重物，当风力小的时候，调节重物靠近转轴，这样r就减小了，导致J减小，因为M是一定的，所以风车的角加速度就会增大，风车转动速度就会变快，效率更高。当风大的时候亦是如此，相反操作就可以实现。

3.最后一个知识点：M和w之间存在什么关系？

由上一部分我们可以知道，根据转动定律：M=Ja，a是角加速度，所以a=dw/dt，将dt移到左边可得：Mdt=Jdw,r然后两边求积分即可

最后得到的方程可以类比为动量和冲量之间的方程，在一定的时间内，对F求积分，得到的的就是冲量，等于动量的变化量。当然，在一定的时间内对合外力矩求积分，就是合外力矩冲量，等于角动量的变化量。

接下来思考两个问题：

问题1：

在徒手劈砖头时，为什么将砖头平放在桌子上不容易劈开，将砖头向上翘起一定的角度，却可以轻松劈开？

答：当砖头平放在桌子上时，用手劈砖头时并没有发生转动，因此w很小，且J是一定的，又因为桌子对砖头的合外力矩=JΔw，Δw几乎为0，所以合外力矩很小，砖头不容易被劈开。

当向上翘起一定的角度时，用手劈砖头就会发生转动，砖头在转动的过程中具有w，当砖头碰到桌子一瞬间，w=0，因此，在这个过程中Δw很大，J是一定的，所以桌子对砖头的合外力矩很大，砖头轻松就被劈开。

那么还有人会问，就不用考虑人的手和砖头自身重力的力矩吗？

回答是不用的，相比于桌子给的力矩，其他力矩都很小，可以忽略不计。

问题2：

为什么跳水运动员刚开始跳水时下落速度很快，快接近水面，打开身子时却又下落的很慢？

答：刚跳水时，运动员身体蜷缩在一起，因此r特别小，所以J就很小，因为合外力矩是一定的，所以w就特别大，下落的相对较快，当运动员身子展开时，r增大，J增大，合外力矩一定，w就很小，所以下落的相对较慢。（J=m*r^2）。