一、完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例1:

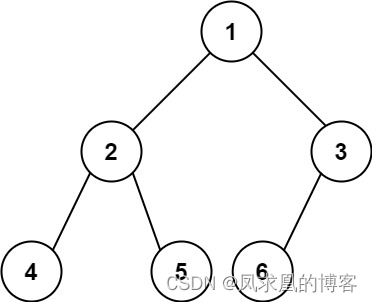
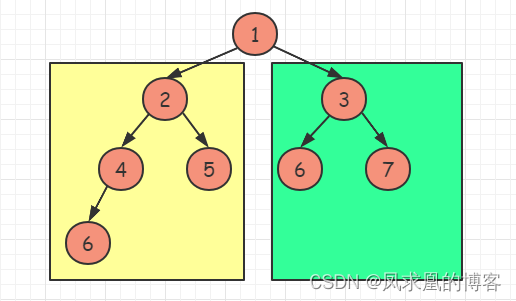
这是一棵完全二叉树：除最后一层外，其余层全部铺满；且最后一层向左停靠

• 如果根节点的左子树深度等于右子树深度，则说明 左子树为满二叉树
  
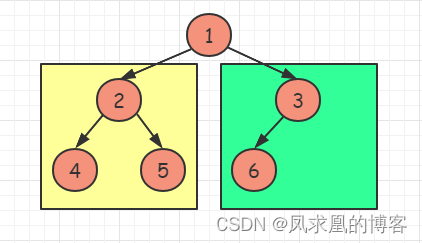
• 如果根节点的左子树深度大于右子树深度，则说明 右子树为满二叉树
  
• 如果知道子树是满二叉树，那么就可以轻松得到该子树的节点数目：(1<<depth) - 1; depth为子树的深度；为了加快幂的运算速度，可以使用移位操作符
• 接着我们只需要接着对另一子树递归即可
• 时间复杂度为 O(logn∗logn)O(logn * logn)O(logn∗logn)，空间复杂度为
  O(1)O(1)O(1)【不考虑递归调用栈】

class Solution:def countLevel(self, node):level = 0while node:level += 1node = node.leftreturn leveldef countNodes(self, root: Optional[TreeNode]) -> int:if not root: return 0left_level = self.countLevel(root.left)right_level = self.countLevel(root.right)# 左子树深度等于右子树深度, 左子树是满二叉树if left_level == right_level:# 满二叉树节点数和level的关系是2^level - 1, 即: 1 << left_level - 1, 为什么+1, 加上root这层return self.countNodes(root.right) + (1 << left_level - 1 + 1)else:return self.countNodes(root.left) + (1 << right_level - 1 + 1)

二、平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

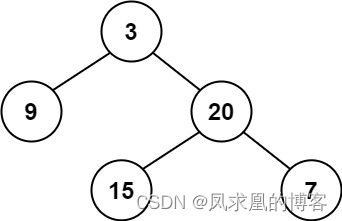
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

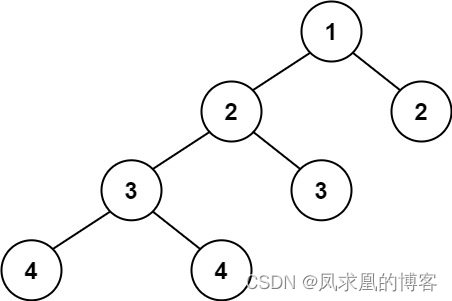
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

class Solution:def isBalanced(self, root: Optional[TreeNode]) -> bool:return self.dfs(root) != -1def dfs(self, node):# node is null, depth == 0if not node: return 0left = self.dfs(node.left)# if -1, 左子树存在高度差大于等于2的情况, 直接返回if left == -1: return -1right = self.dfs(node.right)# if -1, 右子树存在高度差大于等于2的情况, 直接返回if right == -1: return -1# 高度差小于2则取left tree和right tree的最大depth然后加1，算上本层。返回高度# 高度差大于等于2，则返回-1return max(left, right) + 1 if abs(left - right) < 2 else -1

三、二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

• 结点左子树中所含节点的值 小于等于 当前节点的值
• 结点右子树中所含节点的值 大于等于 当前节点的值
• 左子树和右子树都是二叉搜索树

示例 1：

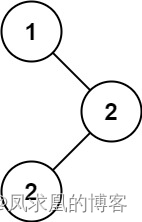
输入：root = [1,null,2,2]
输出：[2]

class Solution:def findMode(self, root: Optional[TreeNode]) -> List[int]:self.max_rate, self.nums = 0, []self.cur_rate, self.cur_num = 0, Noneself.dfs(root)return self.numsdef dfs(self, node):if node:self.dfs(node.left)if self.cur_num == None or self.cur_num == node.val:self.cur_rate += 1else:self.cur_rate = 1self.cur_num = node.val# 注意这个判断要在前面, 不然下个判断的self.max_rate = self.cur_rate# 会造成两次判断都生效，或者用elif代替两次ifif self.cur_rate == self.max_rate:self.nums.append(node.val)if self.cur_rate > self.max_rate:self.max_rate = self.cur_rateself.nums = [node.val]self.dfs(node.right)

四、二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

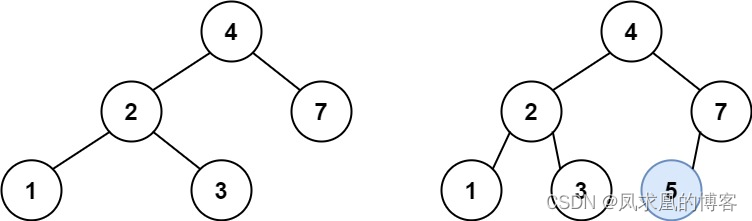
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]

解释：另一个满足题目要求可以通过的树是：

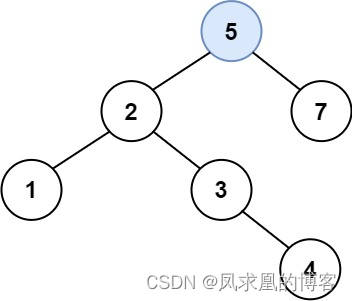
class Solution:def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:if not root: return TreeNode(val)if val < root.val:root.left = self.insertIntoBST(root.left, val)else:root.right = self.insertIntoBST(root.right, val)return root

五、修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

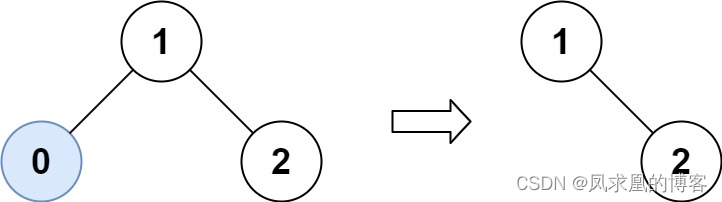
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

class Solution:def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:if not root: returnif low > root.val:return self.trimBST(root.right, low, high)elif high < root.val:return self.trimBST(root.left, low, high)else:root.left = self.trimBST(root.left, low, high)root.right = self.trimBST(root.right, low, high)return root