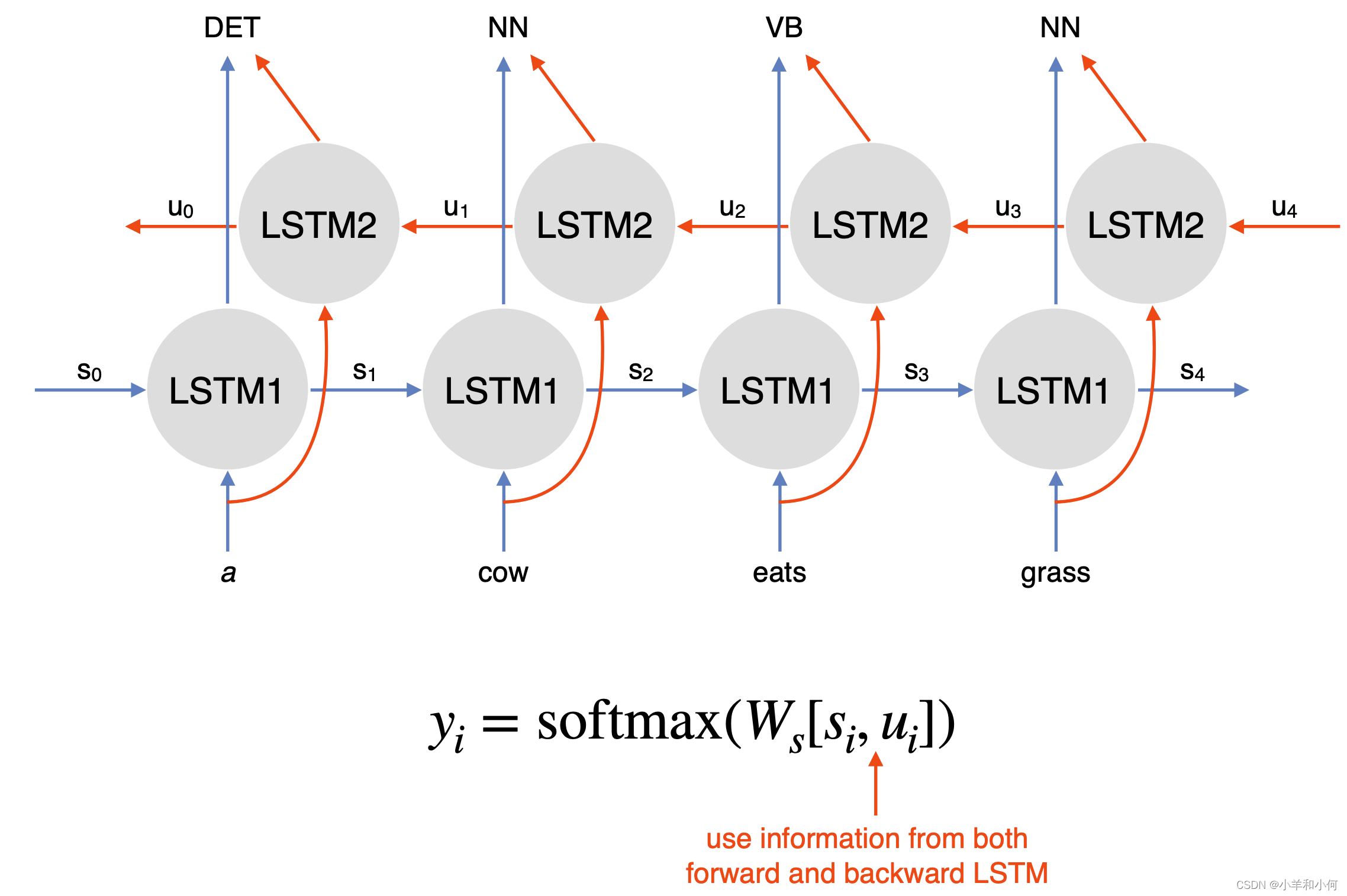
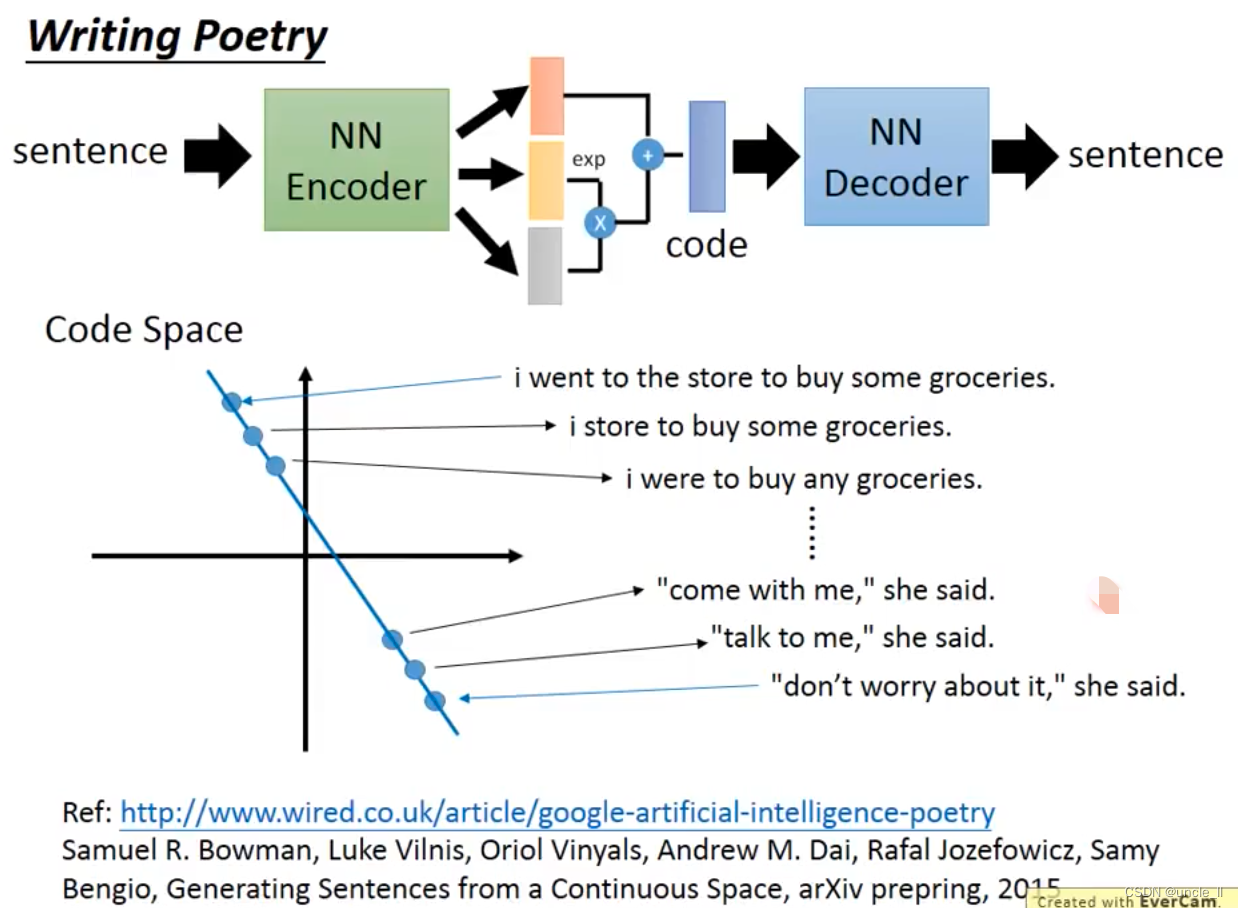
光度立体法检测

图像辐照度

决定场景表面片辐射的因素有两个:

1.在场景表面片的照明

投在某一特定表面片上的照明量取决于该表面片在场景中相对于光源的分布位置

2.表面片反射的入射照明部分

在某一特定方向上被表面片反射的入射照明部分取决于表面材料的光学特性

反射类型:

1.Lambertian反射(也叫理想散射)

Lambertian 表面是指在一个固定的照明分布下从所有的视场方向上观测都具有相同亮度的表面，Lambertian表面不吸收任何入射光.Lambertian反射也叫散光反射，不管照明分布如何，Lambertian 表面在所有的表面方向上接收并发散所有的入射照明，结果是每一个方向上都能看到相同数量的能量.

Lambertian 表面的 BRDF 是一个常数：
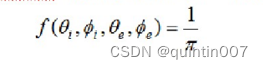
在这里插入图片描述
假定照明不是一个点光源，而是在所有方向都是均匀的，其发光总强度为I.那么亮度可由下式给出:

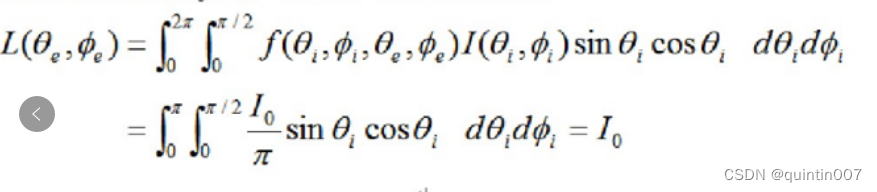
现在，Lambertian 表面的被感觉的亮度在所有方向上都相,这是因为不管表面片朝向何方，它都能接收到同样数量的照明。
表面反射特性：
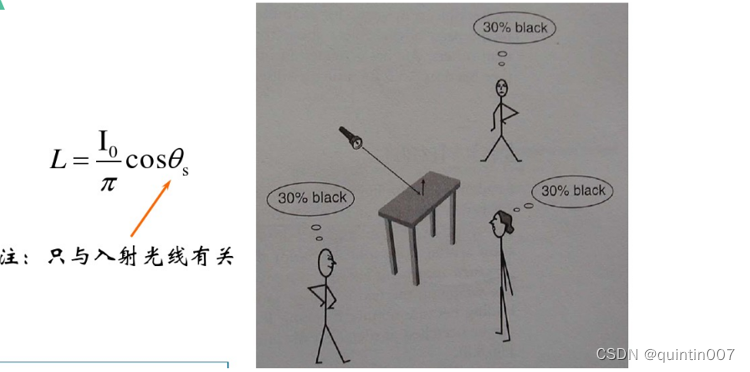
在这里插入图片描述

2.理想镜面反射

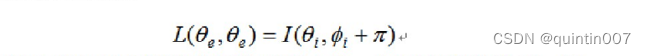
在这里插入图片描述

该方程表明入射光线被表面片反射出去，如同理想的镜子一样。
镜面在某一方向上反射所有的入射光，反射方向角相对于镜面法线来说与入射角相等，但在法线的另一侧，镜面的BRDF为：
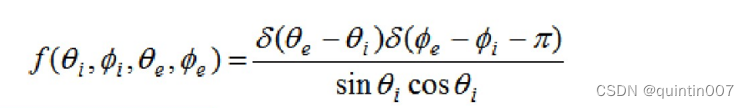
在这里插入图片描述

理想镜面反射特性：

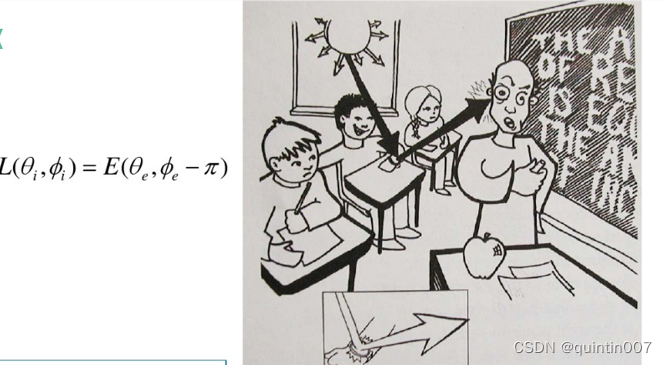
在这里插入图片描述

3.Lambertian反射和镜面反射组合

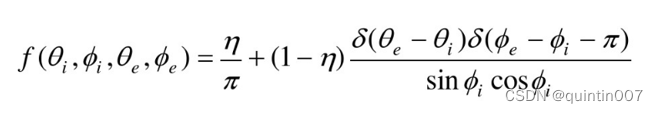
在这里插入图片描述
式中常量控制着两个反射函数的混合度
镜面反射和散光反射的相对比例随着物体表面材料的不同而变化光滑的物体，或者说闪亮的物体，其镜面反射的成分要高于无光泽的物体。

表面方向

想象球上的一个点，并假定一个平面在该点与球相切，该平面的法线也是球上对应点的表面法线。

表面朝向: 表面法线和镜头方向间夹角

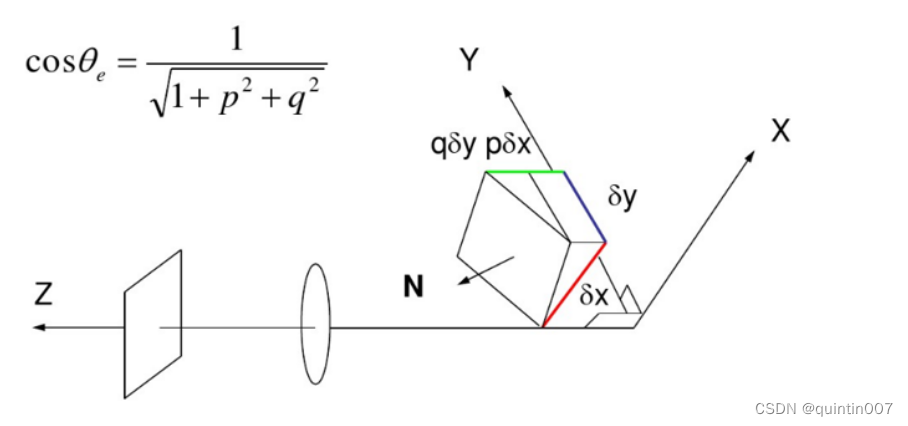
在这里插入图片描述
该式子简单地表明对应于深度z 的单位变化，在X和Y的相应位移量分别为 p和q.单位表面法线可以通过表面法线除以它的长度得到:

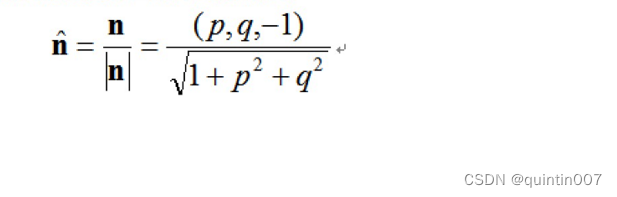
反射图(Reflectance Map)

将场景照明、表面反射和(在以观察者为中心的坐标系中)表面方向表示的组合称为反射图。它确定了在给定照明分布和表面材料的情况下，一个表面片在特定方向上的亮度.
假设具有 Lambertian 反射特性表面片由一个点光源照明。已计算出表面片的辐射为：
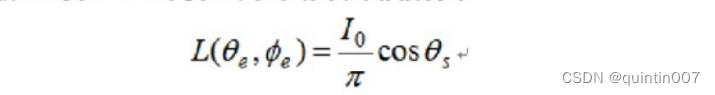
在这里插入图片描述
式中，0.是表面片的法线与光源方向矢量间的夹角。

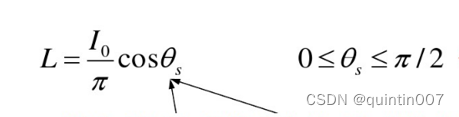
两个矢量间夹角的余弦是两矢量的点积除以每个矢量的长度，所以表面法线和光源方向之间的夹角的余弦是：
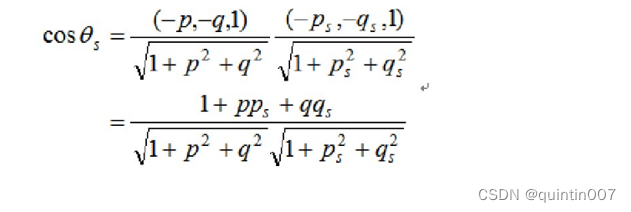
在这里插入图片描述
场景照明 (光源)、表面反射特性和表面方向(梯度表示)共同确定表面一点的亮度，三者的组合形成反射图.
假设图象平面上的辐照度 (亮度) 等于物体表面对应点的辐射度，则已知反射图和以上三个因素，就可以确定图象上一点的亮度。
图像辐照度的精确值取决于各种因素，比如光源强度、光学系统的集光性能以及很多其它不影响反射的因素这些因素使得图像辐照度正比于若干常数。因此，反射图可以归一化，以便统一描述。
这样对于一个远距离点光源照射的朗伯面，有:
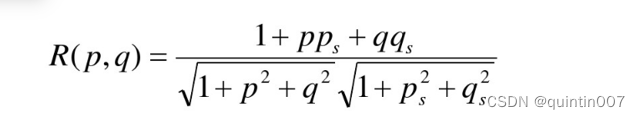
在这里插入图片描述
景物亮度与表面朝向关系可由反射图获得。

点光源照射的Lambertian表面典型反射图

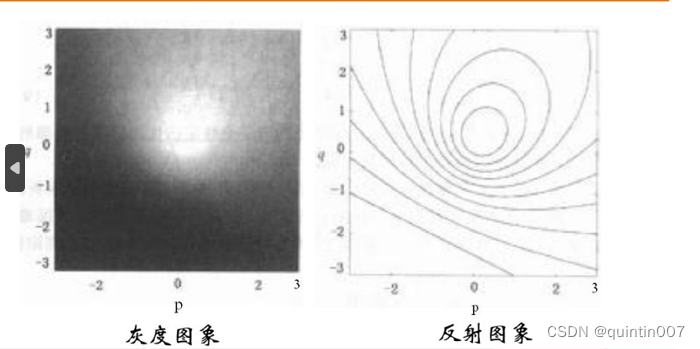
在这里插入图片描述

亮度约束方程

反射图表示了表面亮度与表面朝向的关系。
图像上一个点的辐照度正比于景物中目标表面对应点亮度。
如果归“化将比例系数定为单位值，则可将景物点亮度记为:
可以得到图像上点照度为：
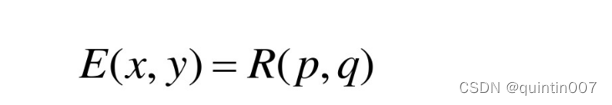
在这里插入图片描述
在一个象素点处的图像强度是对应于场景点的表面方向的函数，该强度值可在反射图中获取。这样，对于一个固定照明和成象条件，以及对于一个已知反射特性的表面，表面方向的变化可转换成图像强度的相应变化。反过来，由图像强度的变化可以恢复表面形状的问题，即所谓从明暗恢复形状的问题。“
图像辐照方程包含有两个未知数,表面方向p和g。
基本思想: 通过不同的光源产生不同的图像辐射方程来增加方程数目，以求解表面方向p和q。假定获取两幅采用不同照明图像，如图所示。这样，对于图像中的每一点，将产生两个图像辐照方程:
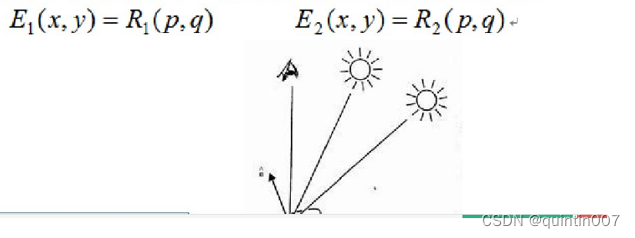
在这里插入图片描述

如果这些方程是线性的，而且是线性无关，则p和9 具有唯一解。如果方程是非线性的，则方程无解或无唯一解。
在两个不同光源照射下的两个反射图迭加示意图：
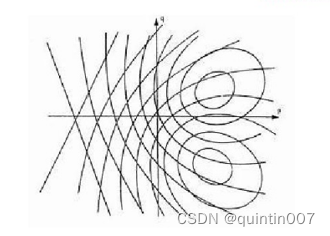
在这里插入图片描述

例如，两个图像辐射方程为:
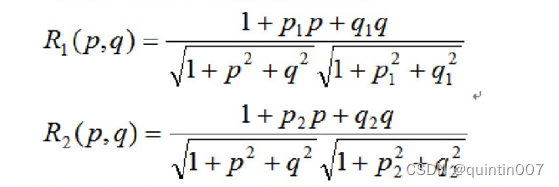
在这里插入图片描述
可以验证，当R和R,分别取不同值时，上述方程将会有一个解、两个解、或无解，当(p1:q1)=(p2;q2)，将有无穷解。
主要代码部分：

ImageFiles := []
ImageFiles[0] :='F:/光度立体/0.jpg'
ImageFiles[1] :='F:/光度立体/90.jpg'
ImageFiles[2] := 'F:/光度立体/180.jpg'
ImageFiles[3] := 'F:/光度立体/360.jpg'* zoom_image_size (Image, ImageZoom, 512, 512, 'constant')
read_image (Image, ImageFiles)
rgb1_to_gray (Image, Image)* Image Acquisition 01: Do something* Tilts := [0,90,180,270]
* Slants := [45,45,45,45]
Tilts := [-80,10,95,-170]
Slants := [45,45,45,45]
* ResultType := ['gradient','albedo']
ResultType := ['gradient']
photometric_stereo (Image, HeightField, Gradient, Albedo, Slants, Tilts, 'gradient', 'poisson', [], [])
derivate_vector_field (Gradient, Result, 5, 'mean_curvature')
* threshold (Result, Regions, 0.001165, 0.1)
threshold (Result, Regions, 0, 0.1)
* gen_circle (ROI_0, 1946.17, 2498.06, 766.33)
* clip_region (Regions, RegionClipped, 1165, 1679, 2744, 3222)