目录
一、最短路径的性质
二、加权有向图的数据结构
(一)、加权有向边数据结构
(二)、加权有向图数据结构
(三)、最短路径API
三、最短路径的算法的理论基础
(一)、最短路径的数据结构
(二)、放松操作
1、放松一条边
2、放松一个顶点
四、最短路径的算法
(一)、Dijkstra算法
1、 Dijkstra算法的代码实现
2、任意点对点之间的最短路径
(二)、无环加权有向图的最短路径算法
1、无环加权有向图的最短路径算法基础
2、加权有向无环图最短路径的代码实现
3、最长路径
(三)、一般加权有向图的最短路径问题
1、相对最后期限限制下的并行任务调度
2、负权重环
3、Bellman-Ford算法
4、套汇
在无向图中寻找最短路径使用广度优先的搜索方法,当边是有向时依然可以用广度优先搜索方法,因为边没有权重,最短路径就是经过最少的顶点到达目标顶点。但是假如边是有权重的时候该方法就不再适用了。(下面的例子跟上面的一句话完全没关系)。
刚下火车站到一个陌生的地方问图书馆怎么走,人家说有两条路
1、沿着这条路走到市政府门口然后右转就到了,这条路稍微远点
2、出火车站往东南方向走进入一个小区,沿着小区里的那条大路走到小喷泉然后右拐,走到8号楼门前在其右前方有个小门,出了小门有个菜市场,走到菜市场中间有个卖猪肉的那里有个后门,从后门出去上大路就能看到图书馆了.......,这条路比上条路少走1公里
对于一个初来乍到的正常人类来讲,通常都会选择第一条路,尽管他会多走一公里,因为第二条路参考点(经过的顶点)太多了,对于正常人来说是不容易记的。
对于第一条路,我们从起点(火车站)出发只途经了一个顶点(市政府),两条边(火车站→市政府,市镇府→图书馆)。如图1所示(该图只是简化,道路可能是曲折蜿蜒的)
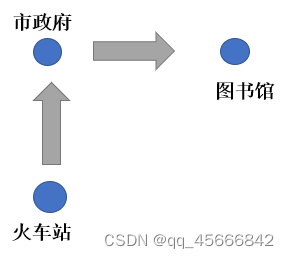
但是对于长期生活在该城市的熟悉这些路的人来说,第二条路是最佳选择,因为走的距离短。
也就是说,对于初来乍到的人,往往不太考虑路的长短(边的权重),只考虑经过的参考点(顶点)是否太多,抽象为有向图。而对于熟悉该地方的人,就不在意经过的参考点(顶点)是多是少,而止考虑路的长短(边的权重),抽象为加权有向图。
其实,在现实生活中,从一个起点到达另一个地点往往有数不清的路线,怎么找到最短的那条路线。或者有的虽然路程短但是堵车严重,找到花费时间最短的那条路径......还有后面要讲的任务调度,套汇等问题,都可以抽象为加权有向图寻找最短路径。而加权有向图寻找起点到各个可达顶点的最短路径,构成一颗最短路径树。
一、最短路径的性质
1、路径是有向的
2、权重不一定等价于距离
3、并不是所有的顶点都是可达的
4、负权重会使问题更复杂
5、最短路径一般都是简单的,不含有环
6、最短路径不一定是唯一的
7、可能存在平行边和自环
二、加权有向图的数据结构
(一)、加权有向边数据结构
加权有向边有三个基本属性,起点,终点,权重。其API如下

public class DirectedEdge {private final int from;private final int to;private final double weight;public DirectedEdge(int v,int w,double weight){this.from = v;this.to = w;this.weight = weight;}public int from(){return from;}public int to(){return to;}public double weight(){return weight;}public String toString(){return String.format("%d->%d %.2f",from,to,weight);}public static void main(String[] args){DirectedEdge e = new DirectedEdge(0,1,0.23);System.out.println(e);}
}
(二)、加权有向图数据结构

public class EdgeWeightedDigraph {private final int V;private int E;private Bag<DirectedEdge>[] adj;@SuppressWarnings("unchecked")public EdgeWeightedDigraph(int V){this.V = V;this.E = 0;adj = (Bag<DirectedEdge>[]) new Bag[V];for(int i=0;i<V;i++){adj[i] = new Bag<DirectedEdge>();}}public EdgeWeightedDigraph(In in){this(in.readInt());int E = in.readInt();for(int i=0;i<E;i++){int v = in.readInt();int w = in.readInt();double weight = in.readDouble();addEdge(new DirectedEdge(v,w,weight));}}public int V(){return V;}public int E(){return E;}public void addEdge(DirectedEdge e){int v = e.from();adj[v].add(e);E++;}public Iterable<DirectedEdge> adj(int v){return adj[v];}public Iterable<DirectedEdge> edges(){Bag<DirectedEdge> edges = new Bag<DirectedEdge>(); for(int v = 0;v<V;v++){for(DirectedEdge e:adj[v])edges.add(e);}return edges;}public String toString(){StringBuilder s = new StringBuilder();s.append(V + " " + E /*+NEWLINE*/);for (int v = 0; v < V; v++) {s.append(v + ": ");for (DirectedEdge e : adj[v]) {s.append(e + " ");}
// s.append(NEWLINE);}return s.toString();}}
(三)、最短路径API

三、最短路径的算法的理论基础
(一)、最短路径的数据结构
首先来看表示最短路径所需的数据结构,跟深度优先算法、广度优先算法和Prim算法一样,用边的数组edgeTo[ ]和double类型数组distTo[ ]来表示,数组索引即是顶点。edgeTo[v]表示的是从起点s到顶点v的最后一条边。像下方中edgeTo[1]表示的是5→1的边,也就是起点0到顶点1的最后一条边,而distTo[1]表示的是从起点0到顶点1的最短路径。
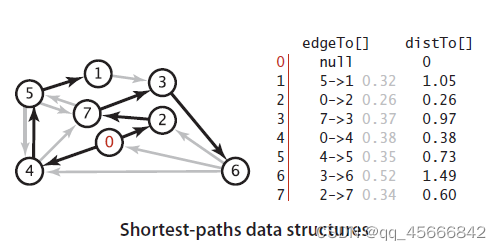
edgeTo和distTo的初始化,edgeTo数组初始时全为空;distTo除了起点初始化为0,其余初始化为无穷大。
(二)、放松操作
寻找加权有向图的最短路径主要是通过“放松”操作,我们定义为relax()函数。
1、放松一条边
private void relax(DirectedEdge e)
{int v = e.from, w = e.to;if(distTo[w] > distTo[v] + e.weight()){distTo[w] = distTo[v] + e.weight();edgeTo[w] = e;}
}如果一条边放松之后改变了数组edgeTo和distTo,那么这条边就是有效边,否则为无效边。
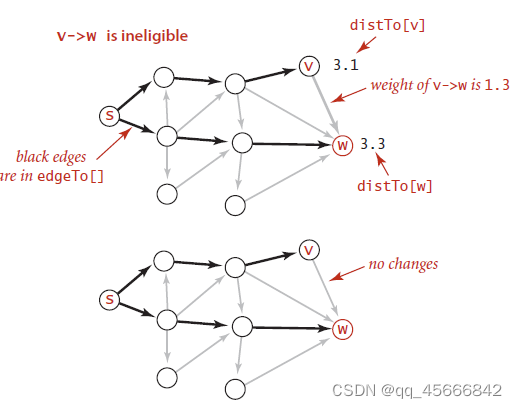
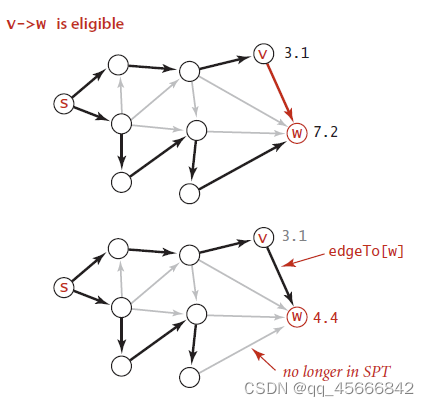
2、放松一个顶点
private void relax(EdgeWeightdedDigraph G,int v)
{for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w] > distTo[v] + e.weight()){edgeTo[w] = e;distTo[w] = distTo[v] + e.weight();}}
}当整个图中不存在有效边时,数组edgeTo表示的就是最短路径树,数组distTo表示的是最短路径长度。
最短路径的最优条件:一幅加权有向图 G, 顶点s是G中的起点。数组distTo[ ]是一个由顶点索引的数组,保存的是G中路径的长度。对于s可达的顶点v,distTo[v]的值是从s到v的某条路径的长度。对于s不可达的顶点,该值无穷大。
当且仅当对于从v到w的任意一条边e,这些值都满足distTo[w] <= distTo[v] +e.weight()时(也就是图中不存在有效边时),distTo数组表示的就是最短路径的长度。
所以找到最短路径的方法就是放松G中的任意边,直到不存在有效边为止。
但是以什么样的顺序放松这些边直到所有边都失效是接下来要讨论的主要问题
四、最短路径的算法
(一)、Dijkstra算法
前面说到,任意放松图中的边直到所有的边都失效即可找到最短路径。我们借鉴最小生成树的Prim算法,逐步往最小路径树中添加边,逐渐生成最小路径树。
首先把distTo[s]初始化为0,其余初始化为正无穷大。然后放松distTo[ ]最小的非树顶点加入树中,直到所有的顶点都在树中或者所有的非树顶点值为正无穷大。但是此算法仅适用于边的权重非负的情况,为什么后续再说。
Dijkstra算法需要的数据结构,除了数组edgeTo和distTo,还需要一个索引优先队列pq,以保存需要被放松的顶点并确定下一个要被放松的顶点,具体步骤如图4所示。
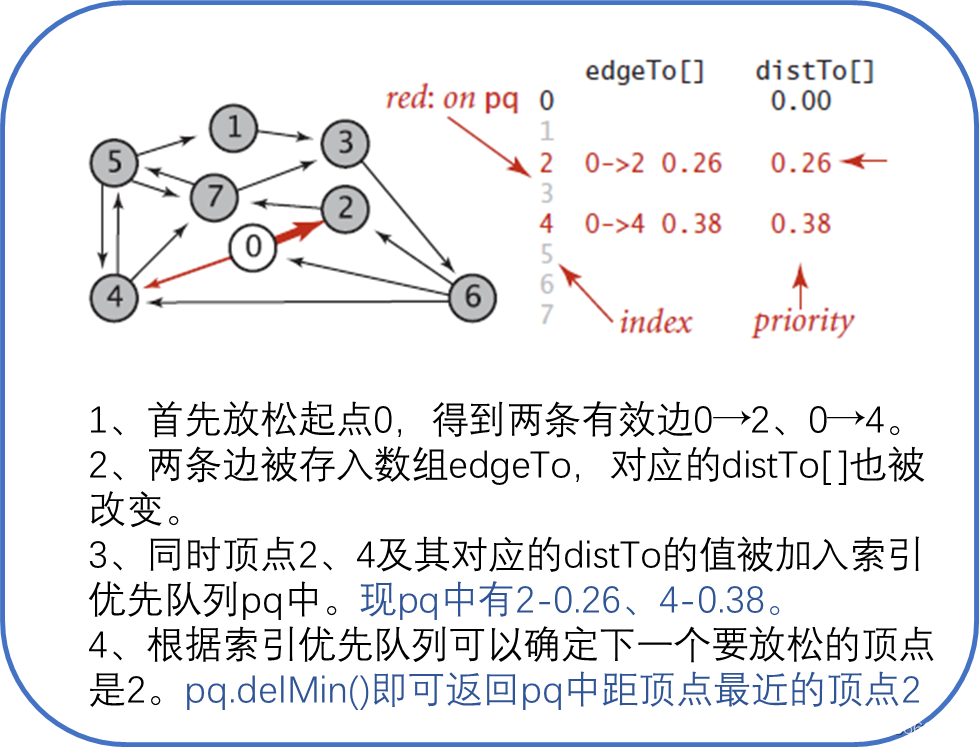
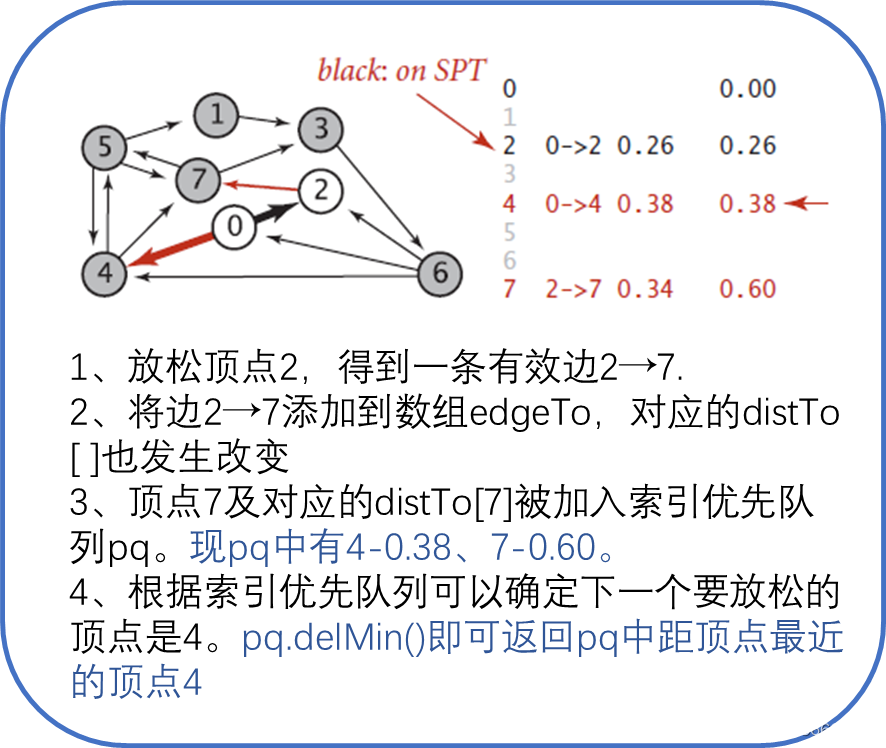
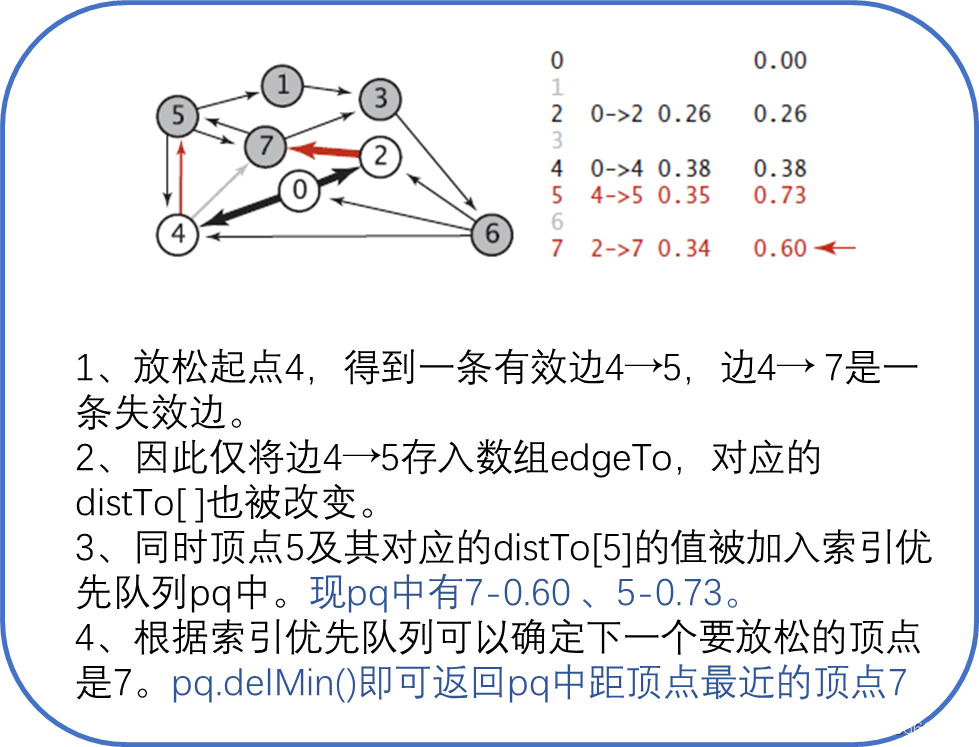
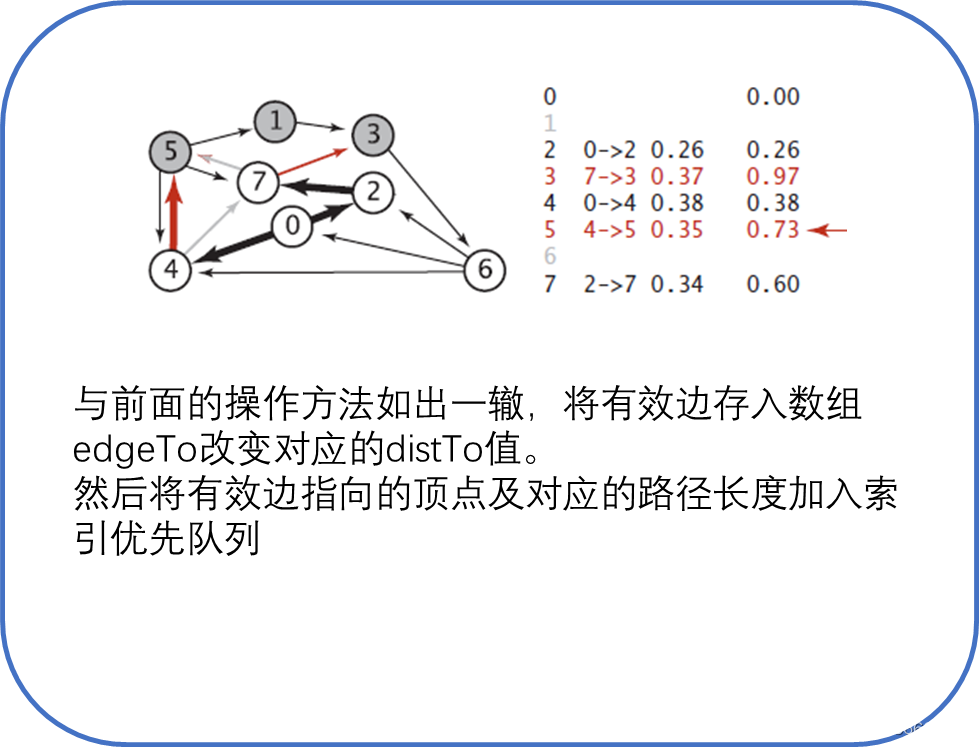
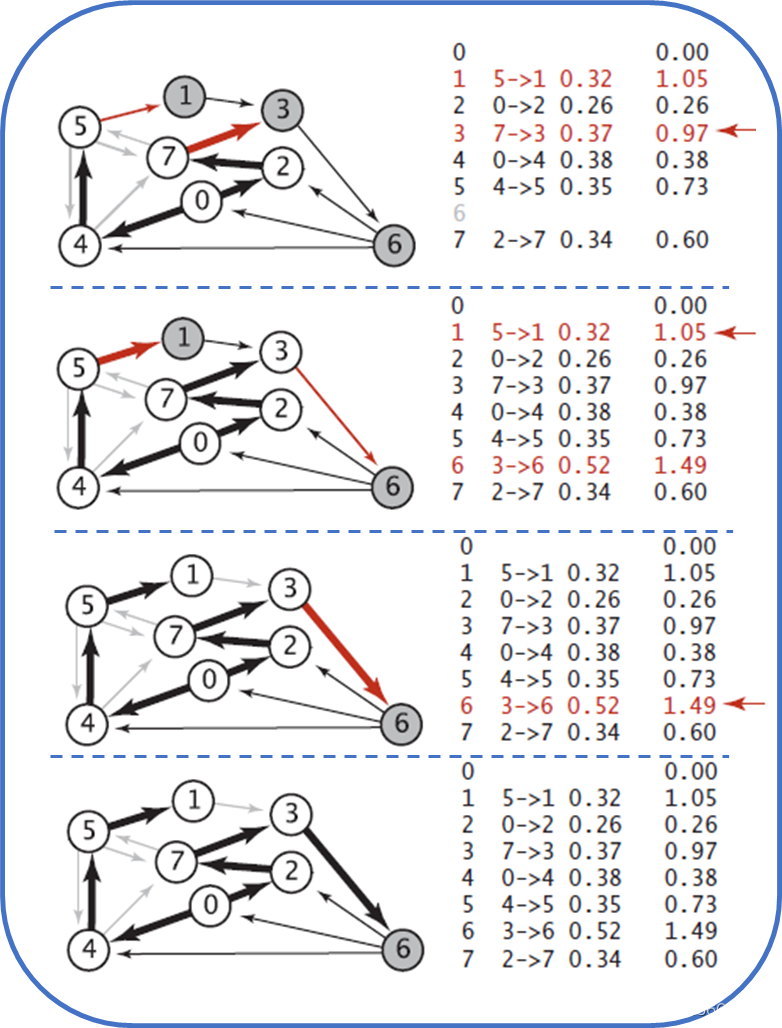
上面几个图太离散,下面的图5更直观简洁
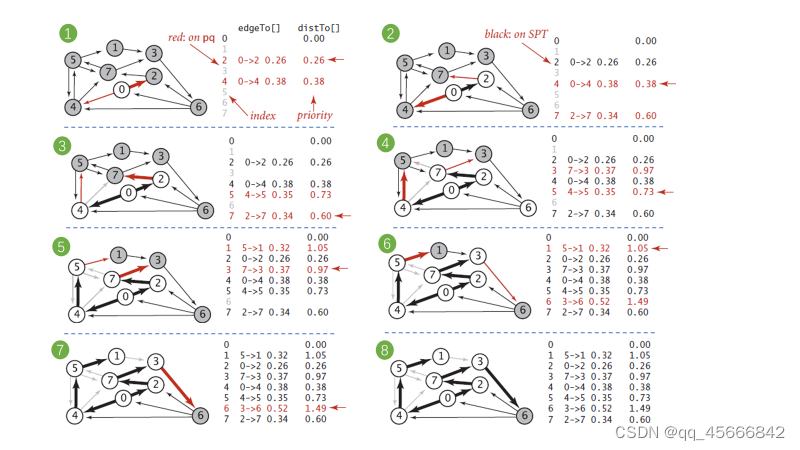
1、 Dijkstra算法的代码实现
public class DijkstraSP
{//该算法所需的数据结构private DirectedEdge[] edgeTo;private double[] distTo;private IndexMinPQ<Integer,Double> pq;}public DijkstraSP(EdgeWeightedDigraph G,int s)
{//构造函数int V = G.V();edgeTo = new DirectedEdge[G.V()];distTo = new double[G.V()];for(int v=0;v<G.V();v++){distTo[v] = Double.POSITIVE_INFINITY;}distTo[s] = 0;pq = new IndexMinPQ<Double>(G.V());pq.insert(0,0.0);while(!pq.isEmpty()){relax(G,pq.delMin());}
}private void relax(int v,EdgeWeightedDigraph G)
{//放松顶点for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w]>distTo[v]+e.weight()){edgeTo[w] = e;distTo[w] = distTo[v]+e.weight();if(pq.contains(w)) pq.change(w, distTo[w]);else pq.insert(w, distTo[w]);}}
} public double distTo(int v){return distTo[v];}public boolean hasPathTo(int v){return distTo[v] != Double.POSITIVE_INFINITY;}public Iterable<DirectedEdge> pathTo(int v){if(!hasPathTo(v)) return null;Stack<DirectedEdge> path = new Stack<DirectedEdge>();for(DirectedEdge e = edgeTo[v];e!=null;e=edgeTo[e.from()])path.push(e);return path;}Dijkstra算法的实现每次为最短路径添加一条边,该边由树中的顶点指向一个非树的顶点w并且w是到s最近的顶点。
2、任意点对点之间的最短路径
public class DijkstraAllPairsSP
{DijkstraSP[] all;public DijkstraAllPairsSP(EdgeWeightedDigraph G){all = new DijkstraSP[G.V()];for(int i=0;i<G.V();i++){all[i] = new DijkstraSP(G,i);}}public Iterable<DirectedEdge> pathTo(int v,int w){return all[v].pathTo(w);}public double distTo(int v,int w){return all[v].distTo[w];}
}(二)、无环加权有向图的最短路径算法
1、无环加权有向图的最短路径算法基础
按照拓扑排序顺序放松顶点,即可得到最短路径树。边的权重为负亦可使用。
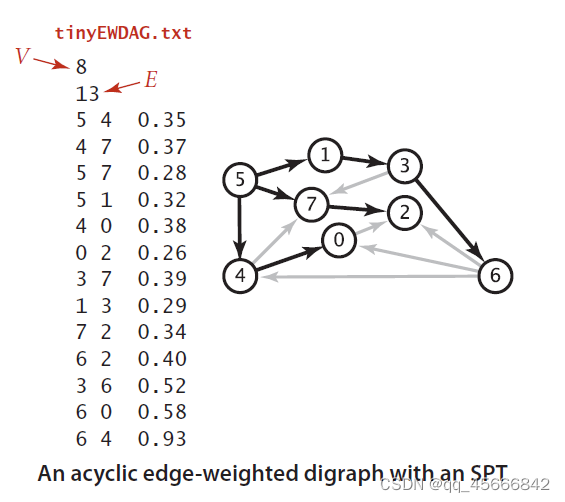
图6的加权有向无环图的拓扑排序为5 1 3 6 4 7 0 2,要得到该图的拓扑排序需要Topological类(该类使用深度优先搜索的方法得到图的图片拓扑排序)
2、加权有向无环图最短路径的代码实现
public calss AcyclicSP
{//该方法所用到的数据结构private DirectedEdge[] edgeTo;//存放指向该顶点的那条边private double[] distTo;
} public AcyclicSP(EdgeWeightedDigraph G,int s){//构造函数edgeTo = new DirectedEdge[G.V()];distTo = new double[G.V()];for(int v=0;v<G.V();v++){distTo[v] = Double.POSITIVE_INFINITY;}distTo[s] = 0.0;Topological tp = new Topological(G);for(int v:tp.order())relax(v,G);} private void relax(int v,EdgeWeightedDigraph G){//放松函数for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w]>distTo[v]+e.weight()){edgeTo[w] = e;distTo[w] = distTo[v]+e.weight();}}} public double distTo(int v){return distTo[v];}public Iterable<DirectedEdge> pathTo(int v){Stack<DirectedEdge> path = new Stack<DirectedEdge>();for(DirectedEdge e = edgeTo[v];e!=null;e=edgeTo[e.from()])path.push(e);return path;}3、最长路径
寻找无环加权有向图中的单点最长路径。
寻找最短路径有实际应用的意义,那么寻找最长路径有什么意义呢?最长路径要解决的问题是优先级限制下的并行任务调度,就是给定一组特定的任务,但是这些任务中有的任务必须在特定任务之后才能进行,有的则可以与其他任务并行处理。比如完成一台电脑生产,显卡、内存、屏幕、芯片等可以有不同的工厂平行同时生产,但是组装必须在这些零件的生产之后。假如生产显卡需要生产的时间最长,那么完成一台电脑的时间最短时间就是生产显卡的时间加上组装的时间(图7所示)。
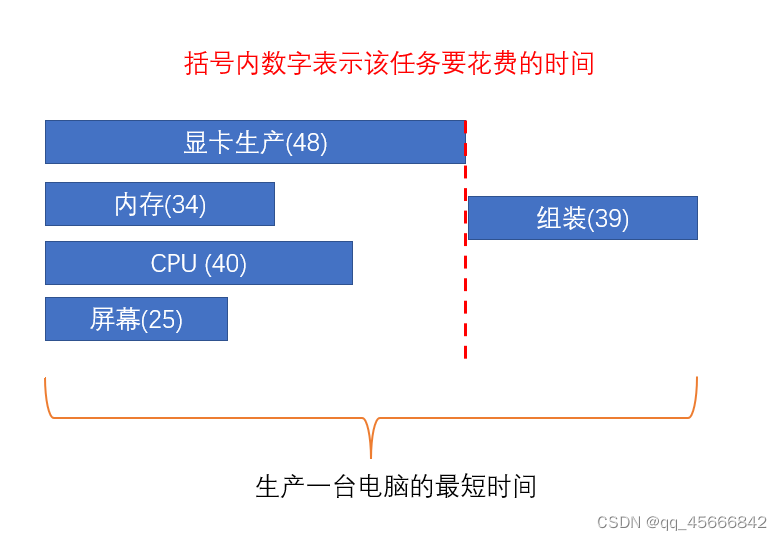
我们把上图抽象为一幅加权无环有向图(如下图8所示)

由上图可见生产一台电脑的最短时间即时上图中s→1→1’→5→5’→t这条路径,所需最短时间是87个时间单位,这条路径是图中的最长路径。
算最长路径的方法很简单,只需要将AcyclicSP(寻找最短路径)中的数组distTo初始化为负无穷,修改relax()函数中不等式方向即可。
private void relax(int v,EdgeWeightedDigraph G){//寻找最长路径的relax函数for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w]<distTo[v]+e.weight()) //修改条件{edgeTo[w] = e;distTo[w] = distTo[v]+e.weight();}}一个任务调度实例
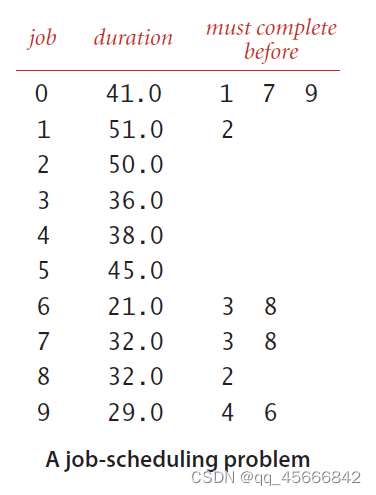
上图是一个任务调度实例,job列表示的是任务代号,duration表示该任务需要花费的时间,最后表示的是该任务必须在这些任务前进行。比如任务0必须在任务1、2、9任务开始前完成。问:完成上述任务需要的最短时间是多少?
通过最长路径算法得出最短时间是173.0个时间单位(如何计算后续再说)。该问题解决方案如下图9所示。
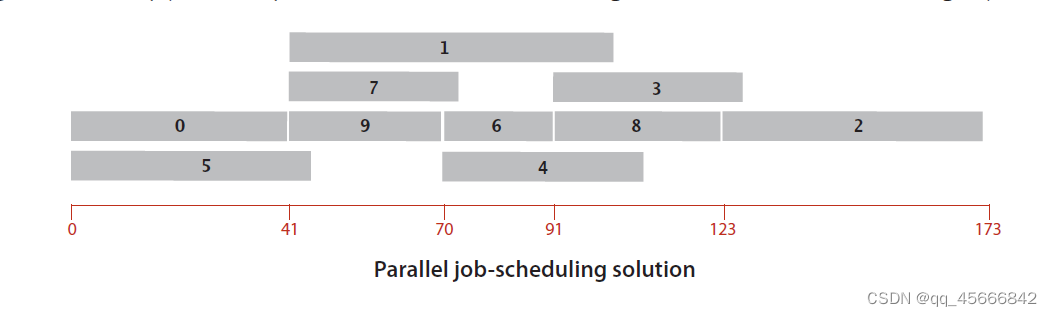
由上图可见,任务必须按照0→9→6→8→2的顺序完成,该任务序列是最长序列,是影响任务完成时间的关键路径。
我们可以把上述问题抽象为一张加权有向无环图,把问题简化为寻找图中的最长路径(如图11所示)。
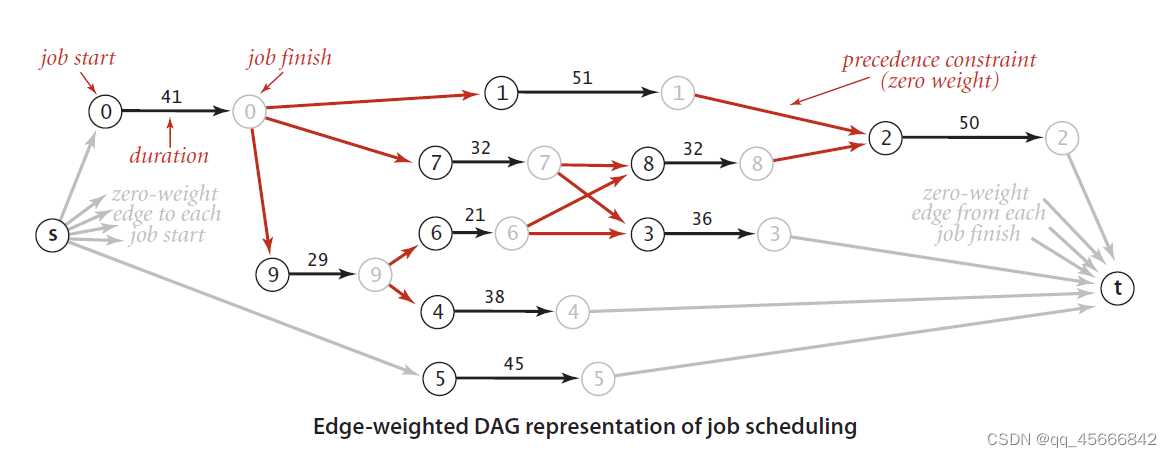
代码实现
public class CPM {public static void main(String[] args) {In in = new In(args[0]);int N = Integer.parseInt(in.readLine());int s = 2*N,t = 2*N+1;EdgeWeightedDigraph G = new EdgeWeightedDigraph(s+2);for(int i=0;i<N;i++){String[] str = in.readLine().split("\\s+");// \s代表一个空白符,但是在Java中反斜杠代表转义,所以需要在前面加一个反斜杠double duration = Double.parseDouble(str[0]);G.addEdge(new DirectedEdge(i,i+N,duration)); //添加代表任务的一条边G.addEdge(new DirectedEdge(s,i,0.0)); //添加从起始s到任务起点的一条边G.addEdge(new DirectedEdge(i+N,t,0)); //添加从任务终点到结束点的一条边for(int j =1;j<str.length;j++){int w = Integer.parseInt(str[j]);G.addEdge(new DirectedEdge(i+N,w,0.0));}}AcyclicLP a = new AcyclicLP(G,s); //寻找最长路径的类,除了relax方法和distTo数组初始化,其余皆与AcyclicSP相同System.out.println("任务开始时间:");for(int i=0;i<N;i++)System.out.println(i+": "+a.distTo(i));System.out.printf("结束时间:%5.1f", a.distTo(t));}}(三)、一般加权有向图的最短路径问题
1、相对最后期限限制下的并行任务调度
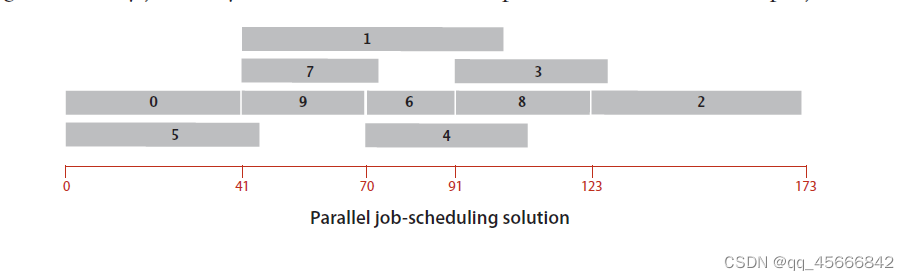
上图是前面描述的并行任务调度的图。原各任务之间只有优先级限制,我们再向其添加相对最后期限限制。如2号任务必须在4号任务启动后的12个单位时间内启动。这个限制看似是限制2号任务,其实是限制的4号任务,因为4号任务可以在5号任务完成之后立即开始,也可以等5号任务完成一段时间后再开始,即4号任务的开始时间不能早于2号任务开始12个时间单位,我们可以令四号任务开始于111时间。如果4号任务耗时很长,可能会延长整个调度计划的完成时间。
对于上述的相对最后期限限制,我们在抽象为加权有向图时,将最后期限限制抽象为一条负权重边。如果任务v必须在任务w启动后的d个单位时间内开始,则添加一条从v指向w的负权重为d的边。上述的“4号任务启动后的12个单位时间内,2号任务必须启动”的限制添加一条从2指向4权重为-12的边。说明负权重边在实际生活中也有实际意义,如何解决带有负权重边并且可能带环的加权有向图的最短路径问题?
2、负权重环
Dijkstra算法只能算非负边的图,因为该算法基于的是“每添加一条边路径都会边长”,这也是为什么Dijkstra算法只能算权重非负的边的图;拓扑排序只适用加权有向无环图;当存在负权重边时,最短路径可能会为了经过负权重边绕路
在解决这个问题之前,先了解一下负权重环-----总权重为负的有向环。
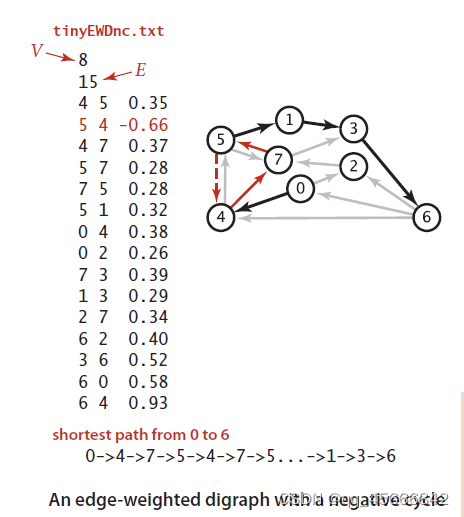
上图中起点为0,从0到各个顶点的最短距离都为负无穷,因为4-7-5是一个负权重环,只需要在这个环无限的绕下去那么到各个顶点的最短距离就是负无穷。所以当起点s到v的路径上有顶点在负权重环上,那么s到v的最短距离就是负无穷。换句话说,负权重环存在的情况下,最短路径没有意义。除非负权重环不可达。
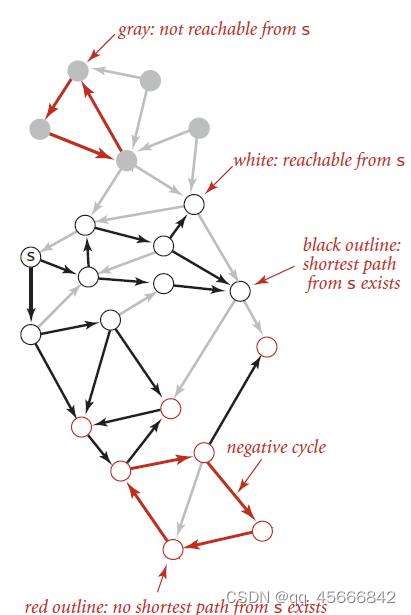
灰色顶点为不可达,白色顶点为可达且有最短路径,红色顶点表示不存在从s到该顶点的最短路径
所以在处理最短路径问题时,负权重环的检测也是一个重要的问题。如何检测负权重环,后面会说。
3、Bellman-Ford算法
在任意含有V个顶点的加权有向图中给定起点s,从s无法到达任何负权重环。distTo[s]初始化为0,其他distTo[ ]元素初始化为无穷大。以任意顺序放松图中的所有边重复V轮,即可得到最短路径树。
for(int pass = 0;pass<G.V();pass++)
{//最外层循环是轮数for(int v = 0;v<G.V();v++){//放松顶点for(DirectedEdge e:G.adj(v))relax(e);}
}这样的话需要放松VE条边,这是效率很低的。怎么改进呢?
只有上一轮的distTo[ ]发生变化的顶点,其指出的边经过放松才能改变其他distTo[ ]的值。我们使用一个先进先出队列来存放这样的顶点。流程如下图13所示。
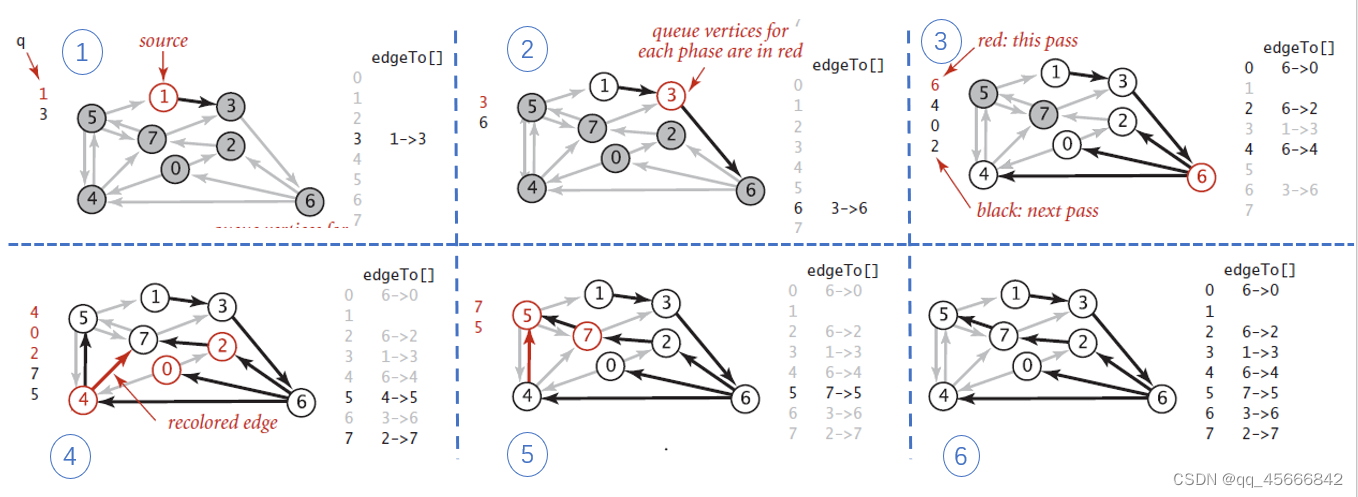
所需要的数据结构也十分简单只需要一个FIFO队列q,和一个布尔数组OnQ[ ]表明定点是否在队列中。首先将起点放入队列q,进入一个循环,然后每次都从队列中取出一个顶点并放松,直到FIFO队列为空。这里的放松函数与之前的略有不同,因为需要将下一轮需要放松的顶点放入队列q,比如上图中放松顶点6后,distTo[6]的值已经改变,那么由顶点6指向的顶点4、0、2的distTo[ ]都会改变,所以要将顶点4、0、2都加入到队列q中。具体的relax()函数代码如下,可以看到还有一个findNegativeCycle()函数,用来判断是否含有负权重环,这个如何实现的,后面再谈。
private void relax(int v,EdgeWeightedDigraph G){for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w]>distTo[v]+e.weight()){distTo[w] = distTo[v]+e.weight();edgeTo[w] = e;if(!onQ[w]){pq.enqueue(w);onQ[w] = true;}}if(count++%G.V() == 0) //放松n次之后检查有无负权重环,该代码设定的是放松V次后检查一次。这个数字不是特别重要,也可以放松一条边就检查一次,但是那样太浪费运行空间和时间。选一个恰当的次数,定期检查。避免资源浪费。{findNegativeCycle(); //寻找负权重环}}}图14的例子中没有负权重边,下图15是含有负权重边的基于FIFO队列的BellmanFord算法
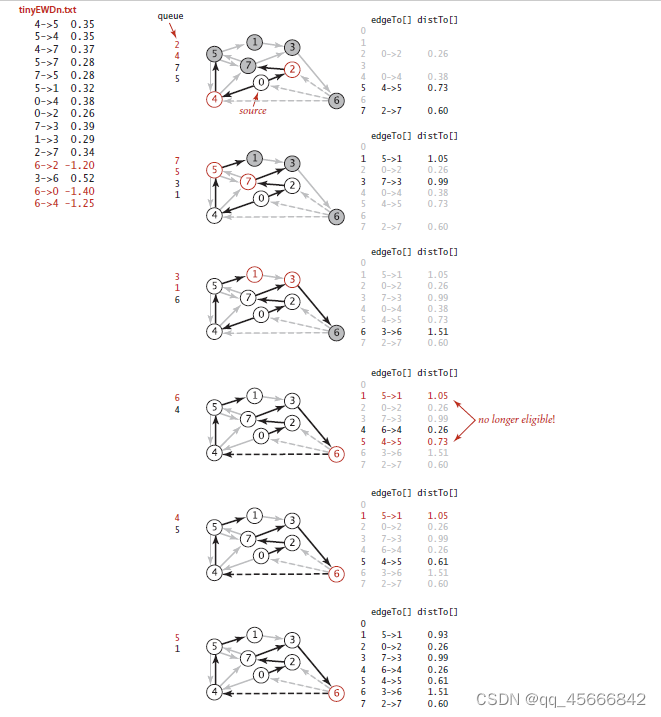
BellmanFord算法代码实现
public class BellmanFordSP
{//该算法所需的数据结构(类的属性)private Queue<Integer> q;private DirectedEdge[] edgeTo;private double[] distTo;private boolean[] onQ;private int count; //记录放松次数private Iterable<DirectedEdge> cycle;//存放负权重环
}public BellmanFord(EdgeWeightedDigraph G,int s)
{int V = G.V();edgeTo = new DirectedEdge[V];distTo = new double[V];OnQ = new boolean[V];q = new Queue<Integer>();for(int v=0;v<V;v++){distTo[v] = Double.POSITIVE_INFINITY;}distTo[s] = 0;q.enqueue(s);OnQ = true;while(!q.isEmpty()&&!this.hasNegativeCycle()){int v = q.dequeue();OnQ[t] = false;relax(G,v);}
} private void relax(EdgeWeightedDigraph G,int v){//具体代码如上所示}public boolean hasPathTo(int v){return distTo[v] != Double.POSITIVE_INFINITY;}public double distTo(int v){return distTo[v];}public Iterable<DirectedEdge> pathTo(int v){Stack<DirectedEdge> path = new Stack<DirectedEdge>();for(DirectedEdge e = edgeTo[v];e!=null;e=edgeTo[e.from()])path.push(e);return path;}private void findNegativeCycle(){//为处理负权重环创建的私有方法...}public boolean hasNegaticeCycle(){//为处理负权重环扩展的最短路径方法...}public Iterable<DirectedEdge> negativeCycle(){//为处理负权重环扩展的最短路径方法...}图14和图15分别描述了BellmanFord算法在非负权重边、含有负权重边的情况。再来看一下图16BellmanFord算法在含有负权重环时的运算轨迹

当所有边放松V轮后队列仍不为空,则说明图中含有从起点可达的负权重环
由上图可知,当图中存在起点可达的负权重环时,FIFO队列q永远不会为空,而且edgeTo[ ]数组组成的子图也包括这个环。所以只要经过一定的放松次数后检查一次edgeTo[ ]数组组成的子图中是否有环,倘若有环则说明存在起点可达的负权重环,将此环返回。
在加权有向图中寻找环的方法代码如下,使用深度优先算法寻找环,
public class EdgeWeightedCycleFinder {private boolean[] marked;private boolean[] onStack;private Stack<DirectedEdge> Cycle;private DirectedEdge[] edgeTo;private boolean hasCycle;public EdgeWeightedCycleFinder(EdgeWeightedDigraph G){edgeTo = new DirectedEdge[G.V()];marked = new boolean[G.V()];onStack = new boolean[G.V()];for(int i = 0;i<G.V();i++){if(!marked[i]) dfs(G,i);}}private void dfs(EdgeWeightedDigraph G,int v){onStack[v] = true;marked[v] = true;for(DirectedEdge e:G.adj(v)){int w = e.to();if(hasCycle) return;if(!marked[w]){edgeTo[w] = e;dfs(G,w);}else if(onStack[w]){Cycle = new Stack<DirectedEdge>(); //这个栈必须在这里初始化,如果在构造函数里初始化,那么Cycle就不为null.hasCycle = true;DirectedEdge f = e;while(f.from() != w){Cycle.push(f);f = edgeTo[f.from()];}Cycle.push(f);}}onStack[v] = false;}public boolean hasCycle(){return hasCycle;}public Iterable<DirectedEdge> Cycle(){return Cycle;}
}根据EdgeWeightedCycleFinder类,我们可以将findNegativeCycle()方法写出来
private void findNegativeCycle()
{EdgeWeightedDigraph spt = new EdgeWeightedDigraph(edgeTo.length());for(int v= 0;v<edgeTo.length();v++){if(edgeTo[v] !=null){spt.addEdge(edgeTo[v]);}}EdgeWeightedCycleFinder cf = new EdgeWeightedCycleFinder(G);this.cycle = cf.cycle();
}由此,hasNegativeCycle()方法和negativeCycle()方法也随之解决
public boolean hasNegaticeCycle(){return cycle != null;}public Iterable<DirectedEdge> negativeCycle(){return cycle;}完整的BellmanFord算法寻找最短路径代码如下
public class BellmanFordSP {private Queue<Integer> pq;private DirectedEdge[] edgeTo;private double[] distTo;private boolean[] onQ;private int count;private Iterable<DirectedEdge> cycle;public BellmanFordSP(EdgeWeightedDigraph G,int s){edgeTo = new DirectedEdge[G.V()];distTo = new double[G.V()];pq = new Queue<Integer>();onQ = new boolean[G.V()];for(int v=0;v<G.V();v++){distTo[v] = Double.POSITIVE_INFINITY;}distTo[s] = 0;pq.enqueue(s);onQ[s] = true;while(!pq.isEmpty()){if(hasNegaticeCycle())break;int i = pq.dequeue();onQ[i] = false;relax(i,G);}}private void relax(int v,EdgeWeightedDigraph G){for(DirectedEdge e:G.adj(v)){int w = e.to();if(distTo[w]>distTo[v]+e.weight()){distTo[w] = distTo[v]+e.weight();edgeTo[w] = e;if(!onQ[w]){pq.enqueue(w);onQ[w] = true;}}if(count++%G.V() == 0) //放松n轮之后检查有无负权重环{findNegativeCycle(); //寻找负权重环}}}private void findNegativeCycle(){int V = edgeTo.length;EdgeWeightedDigraph spt = new EdgeWeightedDigraph(V);for(int i = 0;i<V;i++){if(edgeTo[i] != null)spt.addEdge(edgeTo[i]);}EdgeWeightedCycleFinder cf = new EdgeWeightedCycleFinder(spt);cycle = cf.Cycle();}public boolean hasPathTo(int v){return distTo[v] != Double.POSITIVE_INFINITY;}public double distTo(int v){return distTo[v];}public Iterable<DirectedEdge> pathTo(int v){Stack<DirectedEdge> path = new Stack<DirectedEdge>();for(DirectedEdge e = edgeTo[v];e!=null;e=edgeTo[e.from()])path.push(e);return path;}public boolean hasNegaticeCycle(){return cycle != null;}public Iterable<DirectedEdge> negativeCycle(){return cycle;}
}4、套汇
套汇是指利用不同外汇市场的外汇差价,在某一外汇市场上买进某种货币,同时在另一外汇市场上卖出该种货币,以赚取利润。
比如美元兑欧元的汇率是0.741,即1000美元可以换741欧元;欧元兑加元的汇率是1.366,即741欧元可以换741*1.366 = 1012.206加元;加元兑美元的汇率是0.995,即1012.206加元可以兑换1012.206 * 0.995 = 1007.14497美元。经过以上步骤我们可以看到1000美元经过一系列兑换之后成为了1007.14497美元,多出了7美元左右,这就是套汇。

美元(USD)、欧元(EUR)、英镑(GBP)、瑞士法郎(CHF)、加元(CAD)
图17第s行第t个数字表示一个汇率,表示用1个单位第s行的货币需要多少个单位第t行的货币。比如红色的0.741汇率表示用1美元可以换0.741欧元。
我们刚才说了用美元→欧元→加元→美元,汇率分别为0.741、1.366、0.995

我们将其简化为s→u→t→s这样一条路径(环),汇率即为边的权重,将其抽象为一个加权有向图。我们将边的权重取其自然对数并取反,这样所有边的权重之积的计算就变成了权重之和的计算,w1*w2*w3*...*wn就变成了-ln(w1)-ln(w2)-ln(w3)...-ln(wn)之和。
由此,找到汇率乘积大于1的路径(环),也就成了在加权有向图中找到负权重环,
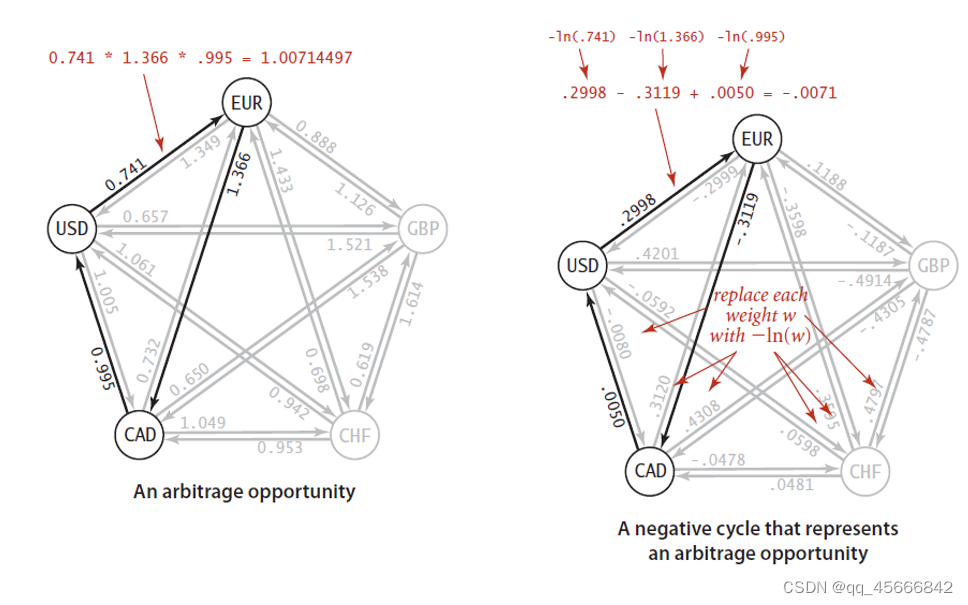
右:取自然对数取负之后的图,问题简化为寻找负权重环
汇率文件格式如下
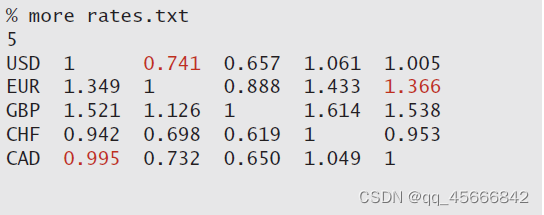
套汇代码实现如下
public class Arbitrage {public static void main(String[] args){//这里使用了算法4里的工具包StdIn,用来读取输入行输入int V = StdIn.readInt(); //货币种类数String[] name = new String[V]; //货币名字数组EdgeWeightedDigraph G = new EdgeWeightedDigraph(V); //创建一个加权有向图for(int i = 0;i<V;i++){name[i] = StdIn.readString();for(int j =0;j<V;j++){double rate = StdIn.readDouble(); //读取汇率DirectedEdge e = new DirectedEdge(i,j,-Math.log(rate));//创建对应的边G.addEdge(e);}}BellmanFordSP spt = new BellmanFordSP(G,0);if(spt.hasNegaticeCycle()){double stake = 1000.0;for(DirectedEdge e:spt.negativeCycle()){StdOut.printf("%10.5f %s",stake,name[e.from()]);stake *= Math.exp(-e.weight());StdOut.printf("=%10.5f %s\n",stake,name[e.to()]);}}else {StdOut.println("没有套汇路径");}}
}