分组密码的定义

定义一个分组密码体制(P, K, C, E, D)，其中P=C={0,1}l ；K={0,1}t .l分组长度;t密钥长度.

加密变换：E：P×K→C, 当k ∈K确定时，Ek为P →C的一一映射.

解密变换：D: C×K →P, 当k ∈K确定时，Dk 为C →P的一一映射.

Dk··Ek =I

柯克霍夫原则

Kerckhoffs假设密码的安全性完全依赖于密钥.

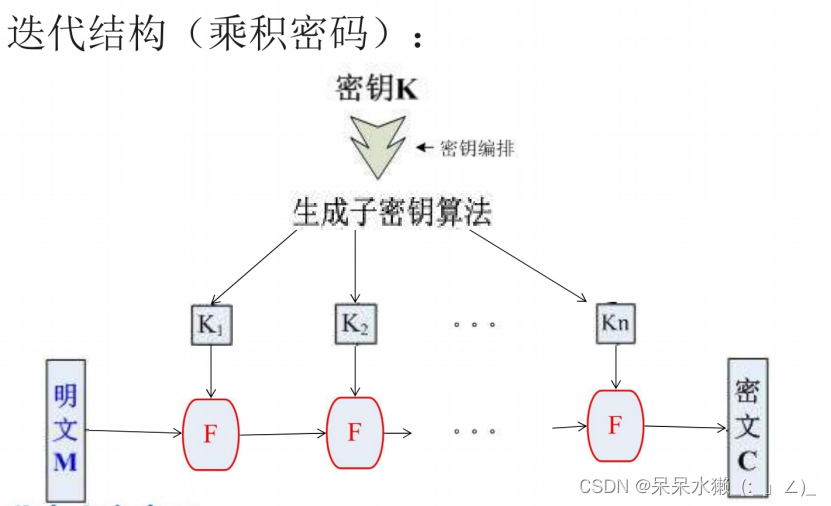
如果密码操作不是幂等的(F2≠F), 那么多次迭代有可能提高密码体制的安全性.

Ø 采用迭代结构的优点：软、硬件实现节省了代码（硬件）资源

混淆：明文/密钥和密文之间的关系复杂

扩散：明文/密钥的每一个比特都影响密文的每一个比特

DES算法概述

Ø 明文和密文分组长度为64比特

Ø 算法包含两部分：迭代加解密和密钥编排

Ø Feistel结构（加解密相似）：加密和解密除密钥编排不同外, 完全相同

Ø 密钥长度：56比特（DES的密钥空间：2^{56}），每7比特

后为一个奇偶校验位（第8位），共64比特

Ø 轮函数采用混乱和扩散的组合，共16轮

AES算法算法概述

Ø 分组加密算法：明文（128比特）和密文分组（128/192/256比特）可变长度。

Ø SPN结构：轮函数包含代换层-置换层-密钥混合层。

Ø 密钥长度：128比特（AES的密钥空间：2^{128}）

Ø 128比特：10轮