模拟退火算法

主要代码

repmat 重复数组副本

B = repmat(A,n) 返回一个数组，该数组在其行维度和列维度包含 A 的 n 个副本。A 为矩阵时，B 大小为 size(A)*n。

unifrnd 生成连续统一的随机数

sort 对数组进行排序

semilogy 半对数图，y 轴有对数刻度

semilogy(X,Y) 在 x 轴上使用线性刻度、在 y 轴上使用以 10 为底的对数刻度来绘制 x 和 y 坐标。

要绘制由线段连接的一组坐标，请将 X 和 Y 指定为相同长度的向量。

要在同一组坐标轴上绘制多组坐标，请将 X 或 Y 中的至少一个指定为矩阵。

semilogy(X,Y,LineSpec) 使用指定的线型、标记和颜色创建绘图。

semilogy(X1,Y1,...,Xn,Yn) 在同一组坐标轴上绘制多对 x 和 y 坐标。此语法可替代将坐标指定为矩阵的形式。

clc;
clear;
close all;%% Problem DefinitionCostFunction = @(x) Sphere(x);    % Cost Function 成本函数nVar = 5;              % Number of Decision (Unknwon) Variables决策数VarSize = [1 nVar];     % Decision Variables Matrix SizeVarMin = -10;           % Lower Bound of Decision Variables
VarMax = 10;           % Upper Bound of Decision Variables%% SA ParametersMaxIt = 1000;     % Maximum Number of Iterations最大迭代次数MaxSubIt = 20;    % Maximum Number of Sub-iterations最大次迭代次数T0 = 0.1;       % Initial Temp.初始温度alpha = 0.99;     % Temp. Reduction Rate温度降低速率nPop = 10;        % Population Size人口规模nMove = 5;        % Number of Neighbors per Individualmu = 0.5;       % Mutation Rate变异率sigma = 0.1*(VarMax-VarMin);    % Mutation Range (Standard Deviation)突变范围（标准偏差）%% Initialization% Create Empty Structure for Individuals
empty_individual.Position = [];
empty_individual.Cost = [];% Create Population Array
pop = repmat(empty_individual, nPop, 1);% Initialize Best Solution
BestSol.Cost = inf;% Initialize Population
for i = 1:nPop% Initialize Positionpop(i).Position = unifrnd(VarMin, VarMax, VarSize);% Evaluationpop(i).Cost = CostFunction(pop(i).Position);  % Cost Function 成本函数% Update Best Solutionif pop(i).Cost <= BestSol.CostBestSol = pop(i);endend% Array to Hold Best Cost Values
BestCost = zeros(MaxIt, 1);    % Maximum Number of Iterations最大迭代次数% Intialize Temp.
T = T0;%% SA Main Loopfor it = 1:MaxIt  %MaxIt最大迭代次数for subit = 1:MaxSubIt   %MaxSubIt最大次迭代次数% Create and Evaluate New Solutionsnewpop = repmat(empty_individual, nPop, nMove);for i = 1:nPopfor j = 1:nMove% Create Neighbornewpop(i, j).Position = Mutate(pop(i).Position, mu, sigma, VarMin, VarMax);% Evaluationnewpop(i, j).Cost = CostFunction(newpop(i, j).Position);endendnewpop = newpop(:);% Sort Neighbors[~, SortOrder] = sort([newpop.Cost]);newpop = newpop(SortOrder);for i = 1:nPopif newpop(i).Cost <= pop(i).Costpop(i) = newpop(i);elseDELTA = (newpop(i).Cost-pop(i).Cost)/pop(i).Cost;P = exp(-DELTA/T);if rand <= Ppop(i) = newpop(i);endend% Update Best Solution Ever Foundif pop(i).Cost <= BestSol.CostBestSol = pop(i);endendend% Store Best Cost Ever FoundBestCost(it) = BestSol.Cost;% Display Iteration Informationdisp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);% Update Temp.T = alpha*T;sigma = 0.98*sigma;end%% Resultsfigure;
%plot(BestCost, 'LineWidth', 2);
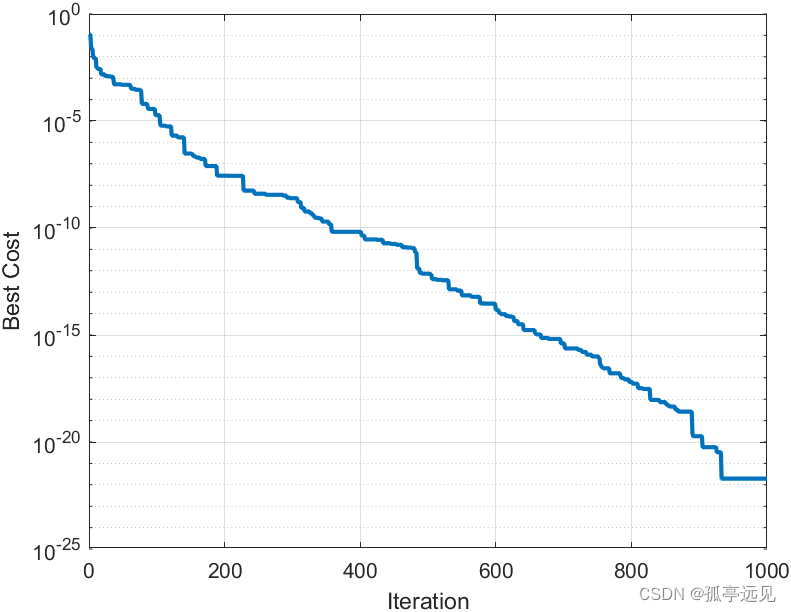
semilogy(BestCost, 'LineWidth', 2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;

Mutate

rand 生成均匀分布的随机数

randn 生成正态分布的随机数

function y = Mutate(x, mu, sigma, VarMin, VarMax)A = (rand(size(x)) <= mu);J = find(A == 1);y = x;y(J) = x(J)+sigma*randn(size(J));% Clippingy = max(y, VarMin);y = min(y, VarMax);end