目录
1. 两数之和 II ★
2. 反转链表 ★★
3. 二叉树的层序遍历 II ★★★
🌟 每日一练刷题专栏
C/C++ 每日一练 专栏
Python 每日一练 专栏
Java 每日一练 专栏
1. 两数之和 II
给定一个已按照 非递减顺序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9 输出:[1,2] 解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
示例 2:
输入:numbers = [2,3,4], target = 6 输出:[1,3]
示例 3:
输入:numbers = [-1,0], target = -1 输出:[1,2]
提示:
2 <= numbers.length <= 3 * 10^4-1000 <= numbers[i] <= 1000numbers按 非递减顺序 排列-1000 <= target <= 1000- 仅存在一个有效答案
代码:
class Solution {public int[] twoSum(int[] numbers, int target) {int[] answer = new int[2];int n = numbers.length;for (int i = 0; i < n - 1; i++) {int t = target - numbers[i];answer[0] = i + 1;for (int j = i + 1; j < n; j++) {if (numbers[j] > t) {break;}if (numbers[j] == t) {answer[1] = j + 1;break;}}if (answer[1] != 0) {break;}}return answer;}
}2. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
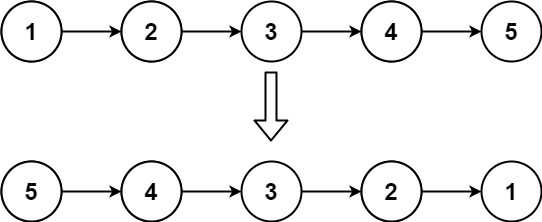
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]
示例 2:
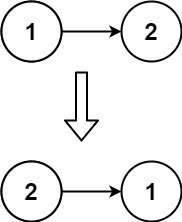
输入:head = [1,2] 输出:[2,1]
示例 3:
输入:head = [] 输出:[]
提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
代码:
public class ListNode {int val;ListNode next;ListNode(int x) {val = x;}
}
class Solution {public ListNode reverseList(ListNode head) {ListNode pre = null;while (head != null) {ListNode tmp = head.next;head.next = pre;pre = head;head = tmp;}return pre;}
}3. 二叉树的层序遍历 II
给定一个二叉树,返回其节点值自底向上的层序遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
例如:给定二叉树 [3,9,20,null,null,15,7],
3/ \9 20/ \15 7
返回其自底向上的层序遍历为:
[ [15,7], [9,20], [3] ]
代码:
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}
class Solution {public List<List<Integer>> levelOrderBottom(TreeNode root) {List<List<Integer>> list1 = new ArrayList<>();if (root == null)return list1;Queue<TreeNode> queue = new LinkedList<>();queue.add(root);while (!queue.isEmpty()) {List<Integer> list2 = new ArrayList<>();int count = queue.size();for (int i = 0; i < count; i++) {TreeNode node = queue.poll();list2.add(node.val);if (node.left != null)queue.add(node.left);if (node.right != null)queue.add(node.right);}list1.add(0, list2);}return list1;}
}附录
DFS 深度优先搜索算法
Depth-First-Search,是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
BFS 广度优先搜索算法
Breadth-First Search,又译作宽度优先搜索,或横向优先搜索,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。
BFS 和 DFS 的区别
1 数据结构
bfs 遍历节点是先进先出,一般使用队列作为辅助数据结构
dfs遍历节点是先进后出,一般使用栈作为辅助数据结构
2 访问节点的方式
bfs是按层次访问的,先访问源点,再访问它的所有相邻节点,并且标记结点已访问,根据每个邻居结点的访问顺序,依次访问它们的邻居结点,并且标记节点已访问,重复这个过程,一直访问到目标节点或无未访问的节点为止。
dfs 是按照一个路径一直访问到底,当前节点没有未访问的邻居节点时,然后回溯到上一个节点,不断的尝试,直到访问到目标节点或所有节点都已访问。
3 应用
bfs 适用于求源点与目标节点距离近的情况,例如:求最短路径。
dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况,例如:全排列、拓扑排序、求到达某一点的任意一条路径。
🌟 每日一练刷题专栏
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
|
| C/C++ 每日一练 专栏 |
|
| Python 每日一练 专栏 |
|
| Java 每日一练 专栏 |