Map和Set
Map和Set是专门用来进行搜索的数据结构,适合动态查找
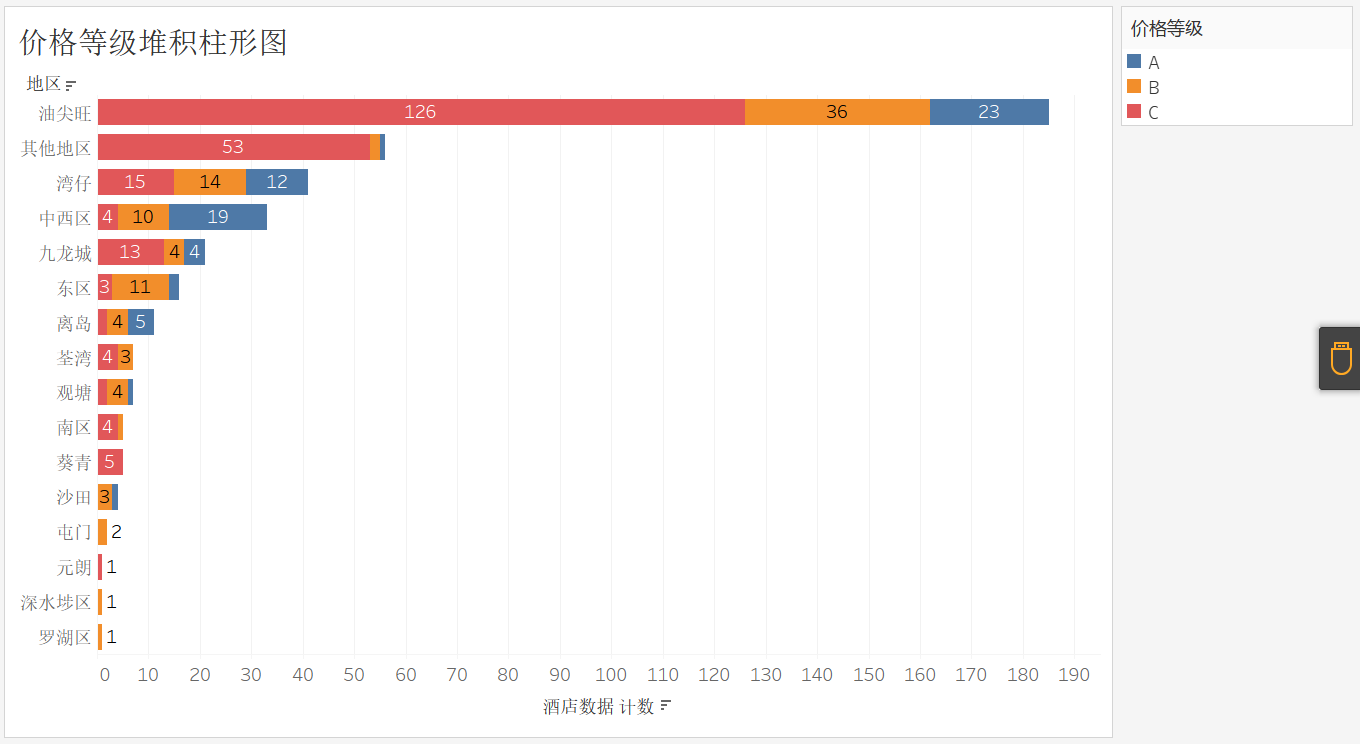
模型
搜索的数据称为关键字(key),关键字对应的叫值(value),key-value键值对
- key模型
- key-value模型
Map存储的就是key-value模型,Set只存储了key
Map
Map是接口类,key是唯一的不能重复
package Map;
import java.util.Map;
import java.util.TreeMap;/*** Created by Y_manyou927* Description:TreeMap实例* User: yyt* Date: 2023-03-10* Time: 14:57*/
public class TestMap {public static void main(String[] args) {Map<String,String> m = new TreeMap<>();// 1.使用put函数添加元素,无序的m.put("孙悟空","齐天大圣");m.put("猪八戒","天蓬元帅");m.put("沙和尚","卷帘大将");System.out.println(m.size());System.out.println(m);
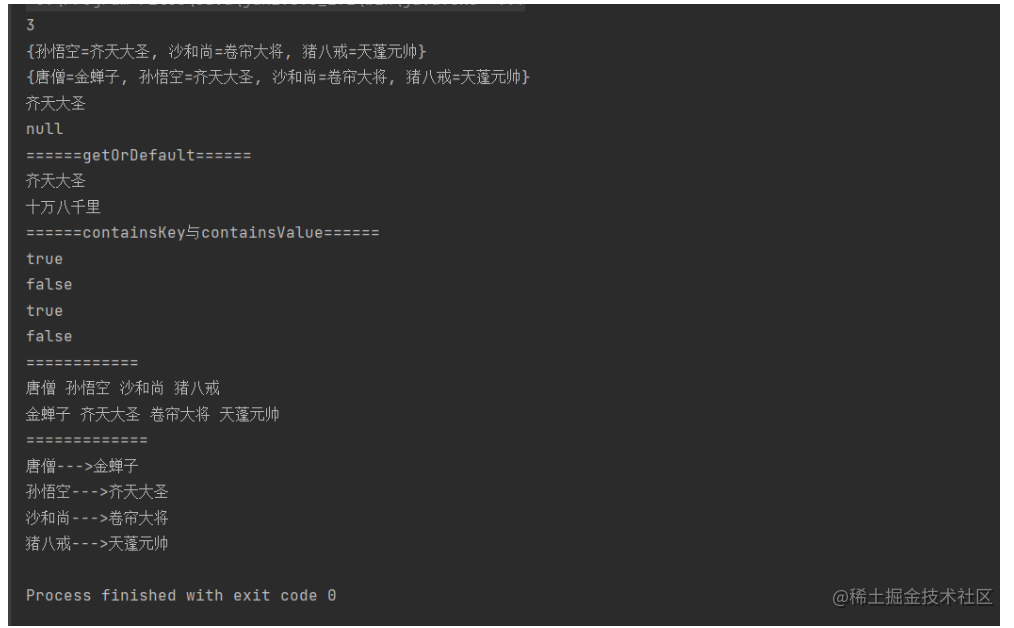
// m.put("唐僧","金蝉子");String str = m.put("唐僧","金蝉子");// 2.如果key存在,可以使用value替换原来的value,key的值不能换,除非删除keym.put("唐僧","师傅");System.out.println(m);// get(key)返回value// 3.如果key存在,返回value,如果不存在,返回nullSystem.out.println(m.get("孙悟空"));System.out.println(m.get("白龙马"));System.out.println("======getOrDefault======");// 4.getOrDefault返回value,如果key不存在,返回一个默认值System.out.println(m.getOrDefault("孙悟空","齐天大圣"));System.out.println(m.getOrDefault("筋斗云","十万八千里"));System.out.println("======containsKey与containsValue======");// 5.containsKey(key)检查key是否包含,时间复杂度O(logN)// 使用红黑树的性质进行查找,存在true,否则falseSystem.out.println(m.containsKey("孙悟空")); //trueSystem.out.println(m.containsKey("二郎神")); //false// containsValue(value)检查value是否包含,时间复杂度0(N)// 6.进行整体遍历,存在true,否则falseSystem.out.println(m.containsValue("齐天大圣")); //trueSystem.out.println(m.containsValue("斗战胜佛")); //falseSystem.out.println("============");// 7.遍历key值与value值for (String s: m.keySet()) {System.out.print(s + " ");}System.out.println();for (String s: m.values()) {System.out.print(s + " ");}System.out.println();System.out.println("=============");// 8.打印所有的键值对// entrySet(): 将Map中的键值对放在Set中返回for (Map.Entry<String,String> entry : m.entrySet()) {System.out.println(entry.getKey()+"--->"+entry.getValue());}}
}
注意:
-
Map是一个接口,不能直接实例化对象,只能实例化其实现类TreeMap和HashMap
-
Map中存放键值对的Key是唯一的,Value可以重复
-
Map插入的键值对Key不能为空,否则会抛出 NullPointerException 异常,Value可以为空
-
Map中的Key可以全部提取出来,存储到Set中进行访问(Key不能重复
-
Map中的Value可以全部提取出来,存储到Collection中的任何一个子集合中
-
Map中键值对的Key不能直接修改,Value可以修改,修改Key只能删除Key,然后重新插入
-
TreeMap与HashMap区别
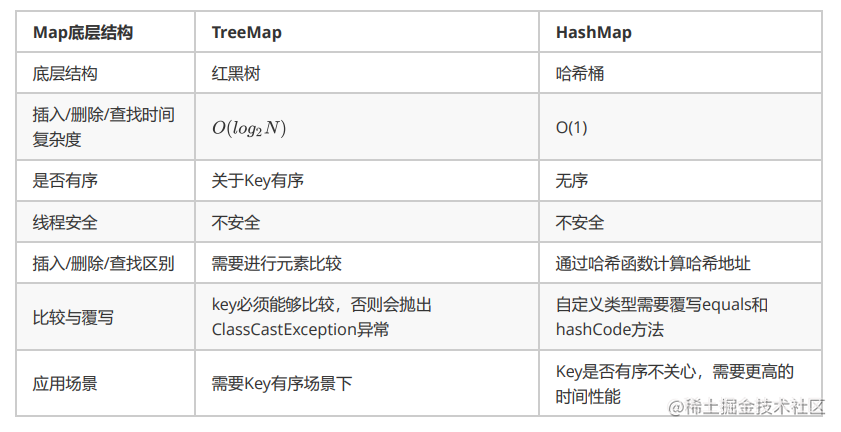
Set
Set与Map的区别:Set是继承Collection的接口类,Set只存储key
package Set;import java.util.Set;
import java.util.TreeSet;/*** Created by Y_manyou927* Description:TreeSet实例* User: yyt* Date: 2023-03-10* Time: 15:37*/
public class TestSet {public static void main(String[] args) {Set<String> s = new TreeSet<>();// 1.add(key) 不存在插入,存在不插入// 返回true 与 falses.add("孙悟空");s.add("猪八戒");s.add("沙和尚");System.out.println(s);boolean b = s.add("孙悟空");System.out.println(b); //falseSystem.out.println("============");// 2.contains(key)判断key是否存在System.out.println(s.contains("孙悟空")); //trueSystem.out.println(s.contains("唐僧")); //false// 3.remove移除存在的元素s.remove("孙悟空");System.out.println(s);System.out.println(s.size());}
}
注意:
- Set是继承自Collection的接口类
- Set只存储到key,并且key要唯一
- Set底层是使用Map来实现的,其使用key与Object的一个默认对象作为键值对插入到Map中的
- Set最大功能就是对集合的元素进行去重
- LinedHashSet是在HashSet的基础上维护了一个双向链表来记录元素的插入次序
- Set的key不能修改,要修改必须先删除然后重新插入
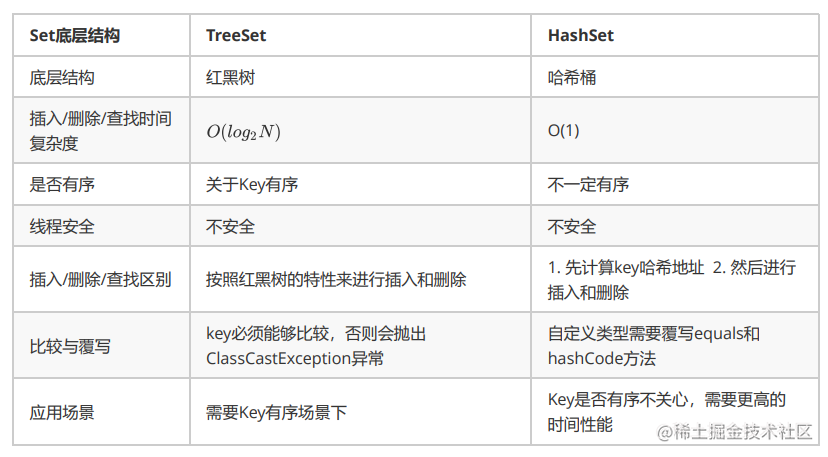
- TreeSet与HashSet区别
哈希表
哈希表,散列表:通过哈希函数使元素的存储位置与它的关键码建立一一映射的关系
- 插入元素:根据元素的关键码,计算元素的存储位置并进行存放
- 搜索元素:对元素的关键码进行同样的计算,所得函数值作为元素的存储位置
哈希方法(散列方法):使用的转换函数称为哈希函数,构造出来的结构称为哈希表(HashTable)
哈希函数设置为:hash(key) = key % capacity ,capacity为存储元素底层空间大小

哈希冲突
哈希冲突:不同关键字通过哈希函数计算出相同的哈希地址
冲突-避免
关键字数量要大于哈希表底层数组的容量,因此哈希冲突是必然会发生的。我们只能降低哈希冲突的发生,或者解决哈希冲突发生产生的问题
1.哈希函数设计
哈希冲突发生的一个原因就可能是哈希函数设计的不合理
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1 之间
- 哈希函数计算出来的地址能均匀分布在整个空间中
- 哈希函数应该比较简单
2.常见哈希函数
- 直接定制法–(常用) 取关键字的某个线性函数为散列地址:Hash(Key)= A*Key + B 优点:简单、均匀 缺点:需要事先知道关 键字的分布情况 使用场景:适合查找比较小且连续的情况
- 除留余数法–(常用) 设散列表中允许的地址数为m,取一个不大于m,但最接近或者等于m的质数p作为除数,按照哈希函数: Hash(key) = key% p(p<=m),将关键码转换成哈希地址
3.冲突-避免-负载因子调节(重点掌握)
负载因子 : A = 表中的元素个数 / 散列表长度
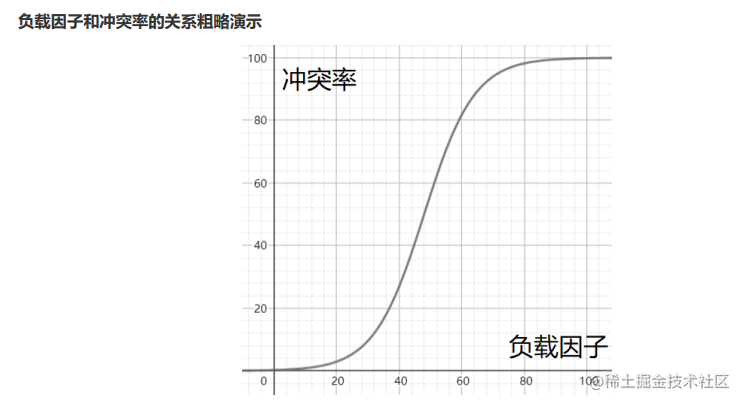
当冲突率达到无法忍受的程度,可以通过降低负载因子来变相降低冲突率。已知哈希表的关键字个数是不可改变的,因此我们只能通过修改数组的长度来达到降低负载因子。
4.哈希冲突-解决
闭散列:开放地址法,当发生哈希冲突的时候,将key存放到冲突的下一个位置
1.线性探测
从发生冲突的位置开始,依次往后进行探测,直到寻找到下一个空位置为止
不能直接删除元素
2.二次探测
线性探测的缺陷就是产生冲突的数据全部堆积在一起,当然这与其找下一个空位置有关
二次探测就是为了避免这种问题
- 闭散列最大的问题就是空间利用率比较低,这也是哈希的缺陷
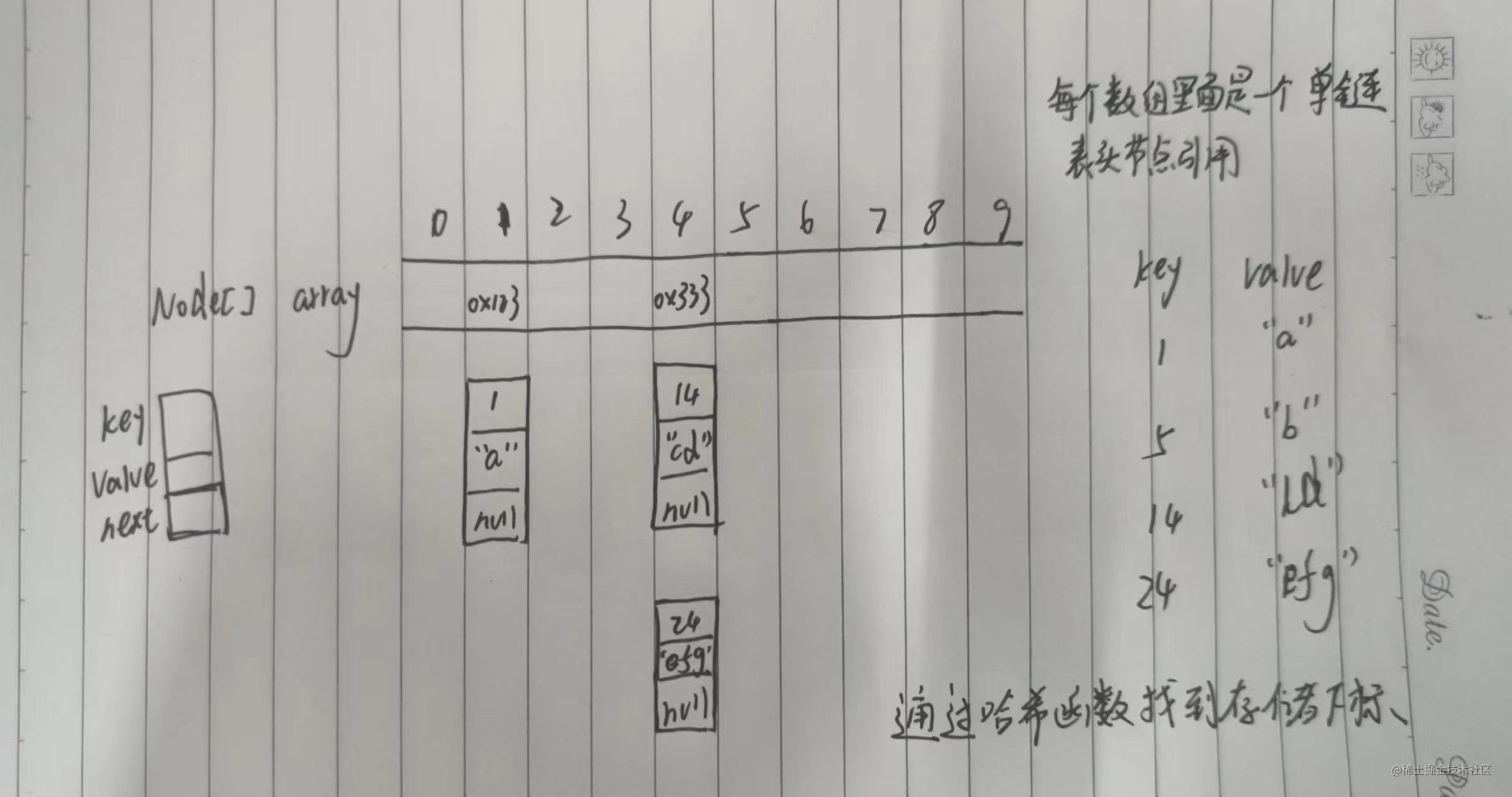
哈希冲突-解决-开散列/哈希桶
开散列法又称为链地址法,将大集合中的搜索问题转化到小集合中进行搜索
JDK1.8开始使用尾插法
当数组的长度超过64且链表的长度超过8,此时链表会变成红黑树
冲突严重时的解决办法
- 每个桶背后是另一个哈希表
- 每个桶背后是一颗搜索树